摘要:从一道题的解答错误点出发，剖析错误原因，给出几种解法，强调不等式运算中“同解变形”的重要性．

　　关键词:不等式运算;“同解变形”;关键

　　高一学生在刚进入高中学习时，学习了一些简单的不等式知识，对于不等式的性质和运算往往用等式的性质和运算来操作，而且出现了错误后还不清楚错在什么地方，笔者近期在为学生布置课后练习时，有这样一道练习题:

　　题目已知实数a，b满足－3≤a+b≤2，－1≤a－b≤4．

　　(1)求实数a，b的取值范围;

　　(2)求3a－2b的取值范围．

　　对于这道练习题，有的学生做出了结果，但解答是不正确的，有些学生解答的结果本身就是错误的，这些学生还不知道是为什么，自已也找不出原因，这究竟是怎么回事呢?下面列举两种典型的错误作一点分析，并对原题给出几种解答，仅供参考．

　　由于结果是单独要求实数a，b的取值范围，所以无可厚非．

　　对于(2)问，由于在运算中，应用了(1)问的非同解变形的结果或再一次进行了非同解变形运算，从而造成错误解答．也就是说不应当利用扩大了范围的结果或行为进行后续运算．

　　错误原因2前一解法的(2)问，属于推理错误，结果错误;后一解法的(2)问，属于推理错误，结果正确．

　　错误原因3前一解法的(2)问，得到

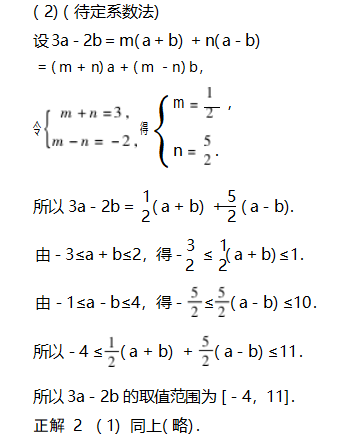
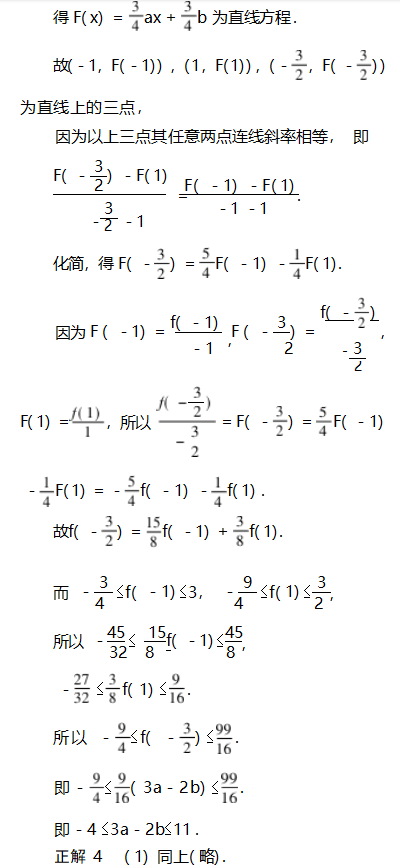
　　(2)(数形结合法)

　　因为在平面直角坐标系aOb中，满足不等式－3≤a+b≤2，－1≤a－b≤4的实数a，b的值构成的点(a，b)形成图1阴影区域．

　　在不等式运算过程中，由于不等式的算理算法并不象等式运算一样很容易做到“同解变形”，虽然许多运算都符合不等式的运算性质，但是稍不留心就会出错，因些，在进行不等式运算时，需要特别注意“同解变形”这个关键问题．

　　参考文献:

　　[1]中华人民共和国教育部．普通高中数学课程标准(2017年版2020年修订)[M]．北京:人民教育出版社，2020．