摘要:多元变量问题因题型多变、形式多样、涉及数学知识面广、蕴含数学思想方法多等特点备受命题者的青睐，本文通过具体实例探讨求解多元变量问题的常用方法，总结归纳一般的求解策略．

　　关键词:多元变量;消参;减元

　　多元变量函数问题是函数中的一大难点，问题类型多样，方法多变，但是解题思路主要把握一个宗旨“消参减元”，再辅以构造新函数进行解题．那么如何消参减元呢?本文主要就两大类型来探讨，一是x1，x2为定义域或所给区间中的任意两个变量;二是x1，x2为函数的零点、极值点或方程的两根．

　　1利用同构式构造新函数以减元

　　评析本题不等式中函数含有两个变量，此类问题的解题思路一般是将两个变量分离至不等式两边，利用同构式可将其转化为函数的单调性问题，构造新函数，利用导数达到“减元”的目的，最终再将问题转化为恒成立问题，通过函数的最值得到解决，考查了逻辑推理、数学建模及数学运算等核心素养．同时要特别注意此类问题在解决时要关注变量的取值范围，以及不等式是对该范围内的任意x1，x2恒成立．

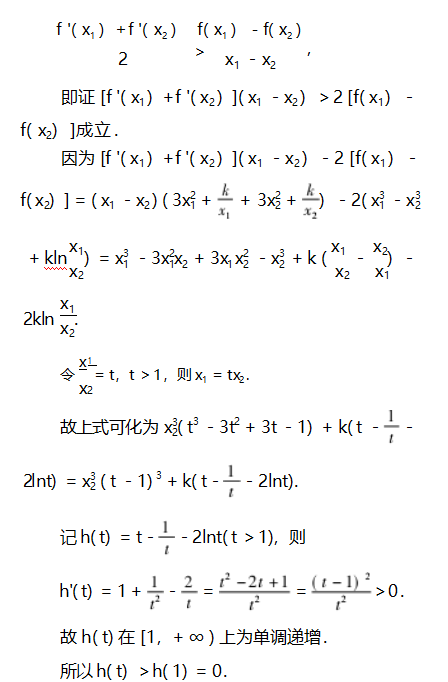
　　4对称变换回归同一单调区间

　　教学中我们不应仅仅是教会学生“这道题”怎么做，更重要的是要引导学生学会对题目条件进行深入挖掘，根据不同条件特征、问题结论等进行方法的选择，当条件特征、问题结论与常见(已掌握)的形式不同时，又应如何转化，如何在解题中真正做到消参减元．在教导通性通法的同时，还应抓住题目条件所包含的信息、知识点与证明结论的转化间的异同及关联，引导学生学会归纳总结其中条件的不同、问题结论的不同与对应方法间的联系，以真正领悟各类方法的数学本质，这样才能真正做到“会一题，通一类”．而这正是对高考评价体系中学科素养所包括的“学习掌握、实践探索、思维方法”3个一级指标的最好践行．

　　参考文献:

　　[1]蔡海涛，卢妮，黄少莹．2020年高考天津卷第20题解法探究[J]．数理化解题研究，2020(31):14－15．