摘要:圆锥曲线是历年高考的必考内容．其中与角度有关的问题，近几年频频出现，牵涉知识较多，包括直线的斜率、相似三角形、解三角形、角平分线、平面向量等内容，综合性强这类问题可以结合等价转化、数形结合等思想，采取一些特殊策略解答．

　　关键词:角度问题;化归转化;数形结合

　　1问题呈现

　　2总体分析

　　解析几何中的角度问题有些可以转化为斜率来处理，比如角度是与坐标轴的夹角;也可以采用余弦定理解答;还可以利用平面向量解答;如果涉及到2倍角关系，还可以采用角平分线的性质或到角公式来进行求解．

　　3试题解答

　　3．1第(1)问解析

　　3．2第(2)问解析

　　视角1借助直线的倾斜角与斜率的关系及正切二倍角公式解答．

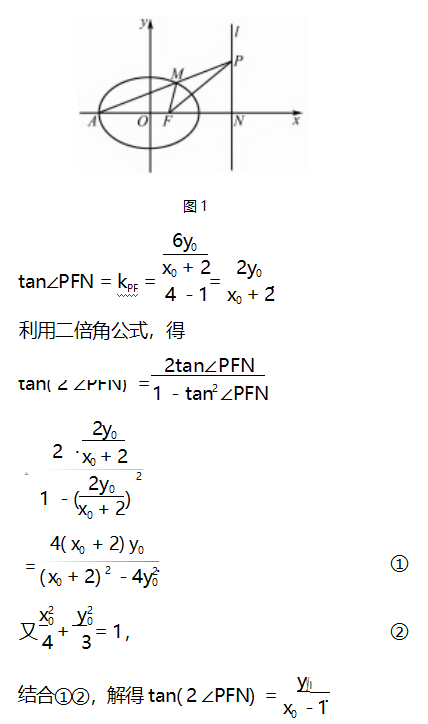
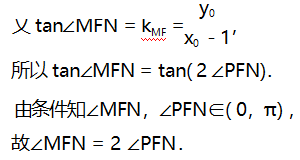
　　评注此解法属于常规解法，要证两角相等，结合角的范围，只需求两角的正切值相等即可．而由图象可知，两角的正切值又与对应直线的斜率密切相关，于是问题等价转化为:先求相关点，再求出相关直线的斜率，即得两角的正切值，最后借助正切二倍角公式进行运算求解即可．这种解法充分体现了化归与转化和数形结合的数学思想．

　　视角2借助到角公式解答．

　　评注现行教材对到角公式不作要求，感兴趣的读者可查阅到角公式，注意公式结构的特征和正切差角公式一致．很多题目用此公式还是切实可行的．建议学有余力的学生掌握，并能灵活运用．

　　视角3利用角平分线的性质解答．

　　视角4借助向量的数量积解答．

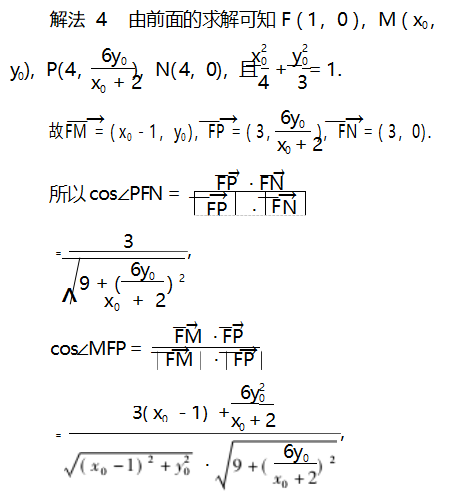
　　评注欲证∠MFN=2∠PFN，结合图象，即证∠MFP=∠PFN，设法找到相关点的坐标，得出对应向量坐标，由向量的数量积公式可得cos∠MFP，cos∠PFN，通过以上求解得到cos∠MFP=cos∠PFN，问题也就迎刃而解了．这也是等价转化的思想．

　　在新课程背景下，课程强调对学生创新精神和实践能力的培养．在教学过程中，多视角、多策略处理问题可以调动学生的积极性，培养他们的思维能力，提高学习效率．而圆锥曲线涉及的概念多、性质多，在解答圆锥曲线类试题时经常会有多种解答方法．因此，在学习这部分知识的过程中，我们要重视一题多解，整合知识，将问题转化为函数、向量、不等式等代数问题来求解．帮助学生完备知识体系，提高学习质量，深挖他们的潜能，培养良好的思维品质．

　　参考文献:

　　[1]胡文文．例谈圆锥曲线中角相等问题的解法[J]．中学数学教学参考，2017(33):36－37．

　　[2]杨宁．挖掘试题的根源培养学生创新思维能力———例谈高中数学圆锥曲线一题多解[J]．知识文库，2018(09):130．