摘要:深度研究高考真题是提高教师专业水平和准确把握教学方向的重要途径，本文对真题进行深入挖掘并作一般性推广，试图把握此类问题的命题规律．

　　关键词:真题;推广;命题规律

　　2021年全国甲卷第20题解析几何中三切线问题的出现感觉耳目一新但又似曾相识，与2011年浙江理数第21题有类似的背景和解法，笔者对这两个问题进行了深度挖掘并作了一般性推广，为读者在教学研究中提供一种思路．

　　1真题呈现

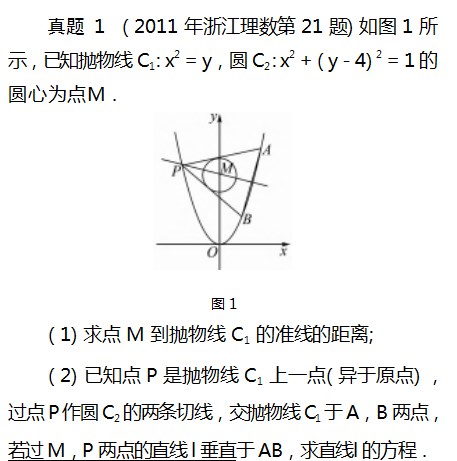
　　2试题解法

　　限于篇幅仅对真题2给出解法．

　　3一般性推广

　　两题均以抛物线上的任一动点向定圆作切线为背景，都可采用同构的思想来解决问题，但2021年全国甲卷第20题显得更为特殊，第三条交点弦仍与圆相切，引起了笔者的思考，现将结论推广到一般的抛物线和椭圆．

　　波利亚说:“要充分利用一般化、特殊化与类比在变更问题方面中的功能．通过对问题的观察、猜测、推广，体会数学发现的过程，提高创造性思维能力．”因此笔者并不满足于得到上述的推广，而是继续深入探索，利用类比的思想将结论进一步推广到椭圆，通过研究，发现椭圆也有如下完全类似的结论．

　　证明同推广2，限于篇幅不再赘述．

　　《普通高中数学课程标准(2017年版)》指出:“数学教育承载着立德树人的根本任务，发展素质教育的功能，数学教育帮助学生掌握现代生活和进一步学习所必须的数学知识、技能、思想和方法，提升学生的数学素养，引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界，促进学生思维能力、实践能力和创新意识的发展．”这对我们一线教师的专业水平提出了更高的要求，而深度研究高考真题，挖掘真题背景是提升教师专业素养、提高教学站位、准确把握教学方向的重要途径．

　　参考文献:

　　[1]波利亚．怎样解题[M]．上海:上海科技教育出版社，2007．

　　[2]中华人民共和国教育部．普通高中数学课程标准(2017年版)[M]．北京:人民教育出版社，2018．