摘要：传统的数学课堂教学多采用讲解接受式的教学方式，重视教师的主导作用而忽视了学生的主体作用，使得学生的学习兴趣不高，“做中学”的教学方式使得这一问题得到了很好的解决，文章通过“做中学”应该遵循的基础性、主体性、趣味性原则对两节勾股定理的教学进行了分析比较，指明了在数学课堂中怎样运用“做中学”理论来进行数学课堂教学．

　　关键词：做中学理论；勾股定理；教学原则

　　《义务教育数学课程标准(2011年版)》中指出：“数学教学应根据具体的教学内容，注意使学生在获得间接经验的同时也能够有机会获得直接经验，即从学生实际出发，创设有助于学生自主学习的问题情境，引导学生通过实践、思考、探索、交流等，获得数学的基础知识、基本技能、基本思想、基本活动经验，促使学生主动地、富有个性地学习，不断提高发现问题和提出问题的能力、分析问题和解决问题的能力．学习数学的最好方式是做数学，因此在数学课堂教学中，就要求授课教师应该根据学生已有的知识状况和心理特点进行教学，让学生亲身经历知识的发生发展过程，充分发挥学生的主体作用，进行知识的再创造，“从做中学”，从而达到改变学生的学习方式的核心理念．

　　1“做中学”的意义

　　“从例中学”作为传统的传授－接受教学法的典型代表，主要是指教师通过言语讲解和操作示范来让学生接受并掌握系统的知识和技能的教学方法．这种教学方法能够在短时间之内较快地让学生掌握所要学习的知识点，比较适用于原有的认知结构比较全面，知识结构比较系统的学生，而且要求学生要有较强的学习主动性和积极性．但是这种教学方式在显示了教师的主导作用，学生的思维活动主要是按照教师的引导方向而发展的，从而很大程度上忽视了学生的主体作用，不能充分调动学生学习的积极性和主动性，禁锢了学生的思维发展．美国著名教育家杜威(John Dewey)以“教育即生活”、“教育即生长”、“教育即经验的改造”为依据，对知与行的关系进行了论述，并提出了举世闻名的“从做中学”(Learning by doing)的理论．在《明日之学校》(School of Tomorrow)一书中，他明确地提出：“从做中学要比从听中学更是一种较好的方法．”在杜威看来，“从做中学”充分体现了学与做的结合，也就是知与行的结合．在数学课堂教学中，运用“做中学”理论进行课堂教学，使得学生成为数学学习中的参与者、探索者，有利于充分发挥学生的主观能动性，调动学生学习数学的主动性和积极性，提高学生认知学习的质量．

　　2基于“做中学”理念下的“勾股定理”课堂教学

　　有着“几何学的基石”之称的勾股定理，作为沟通代数与几何间的桥梁之一，在数学发展中有着无可替代的作用，它是人类文明的共同成果，几乎在各个国家的数学课程中都详细而又不尽相同地介绍了勾股定理，由于不同的文化与史料背景，不同的教师在进行勾股定理教学时所采用的方法各有千秋．

　　2．1苏科版教材下的“勾股定理”教学片段

　　在一节苏科版教材的数学课堂中，授课教师以一系列的问题串入手，开始了勾股定理的教学：

　　师1：同学们，我们已经学过了三角形的一些基本知识，那么如果一个三角形的两条边长分别为8和6，你能够知道第三边的长吗？如果又已知这两边的夹角，那么第三边的长是多少？如果这两边的夹角为直角，那么第三边的长能求出来吗？

　　生：通过刻度尺测量．

　　师1：测量可行吗？没有误差吗？那么如何求出三角形第三边的长？请大家打开学案，完成活动一：在等腰直角三角形中，探究三角形的三边关系．请大家以等腰直角三角形的三条边为边向外作正方形，将所作的正方形沿对角线剪开，拼图探究所作三个正方形的面积关系．

　　学生通过作图，剪纸(如图1，依虚线剪开)拼图活动发现两个小正方形的面积之和等于大的正方形的面积．

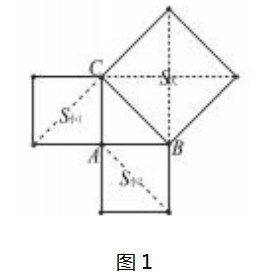
　　师1：请大家思考一下剪纸活动得到的结果有没有严谨的数学推算？

　　生：没有，剪纸存在误差．

　　师1：很好，结果是否正确我们得画个问号，这个三角形是等腰直角三角形，那么刚刚我们所得到的结果是不是对于任意的三角形都适用？下面请大家完成操作活动二：在一般的直角三角形中，探究三角形的三边关系．注意要以格点为顶点任意作一般直角三角形，这里我们不妨取两直角边分别为3和4．同样以直角三角形的三条边为边向外作正方形，来探究一下三角形三边的关系．

　　在学生活动时，教师提示学生通过活动一的方法思考并探究所作三个正方形的面积关系，特别强调如何求斜边上正方形的面积．通过小组合作，教师指导，学生采用割补法作图计算得出了下面两种方式(如图2、图3)求斜边上正方形的面积，并得出了两个小正方形的面积之和等于大正方形的面积这一结果．

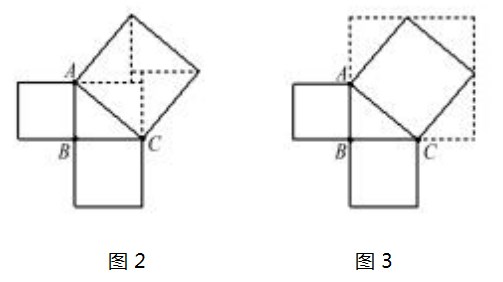
　　在学生探究、交流、讨论之后，教师让学生小组展示，并给与数学推算，最后根据各正方形的面积即为三角形所给各边的平方，进而得到勾股定理，即：直角三角形两直角边的平方和等于斜边的平方．

　　2．2人教版教材下的“勾股定理”教学片段

　　在一节人教版教材的数学课堂中，授课教师以一张1955年希腊发行的一枚纪念邮票入手(如图4)，开始了勾股定理的教学：

　　师2：这是一张邮票，请大家仔细观察这枚邮票上的图案和图案中小方格的个数，你有哪些发现？先不要讨论，自己观察．

　　生：左边正方形小方格个数为16，右边正方形小方格个数为9，下面正方形小方格个数为25．

　　师2：很好，那么大家有没有发现三个正方形的面积有什么数量关系呢？

　　生：两个小正方形的小方格个数之和等于大正方形的小方格个数．

　　师2：好的，其实这三个正方形是由中间的直角三角形以三条边为边向外作正方形所得到的，那么这个直角三角形的三条边有什么样的数量关系呢？下面我们把它放到格点图中，请看格点图(如图5)，每个小方格的面积看作1，那么以BC为一边的正方形的面积是，以AC为一边的正方形的面积是．你能计算出以AB为一边的正方形的面积吗？请通过作图说明你的理由．

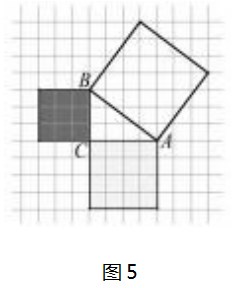
　　学生按照教案上的要求进行探究活动，在学生探究过程中，教师提出疑难之处：如何计算斜边上三角形的面积，在教师引导下，学生的思路逐渐清晰，通过作图思考，合作交流，学生得到了下面的两种方式割补法(如图6、图7)计算斜边上正方形的面积，并通过计算得到两个小正方形的面积之和等于大正方形的面积．

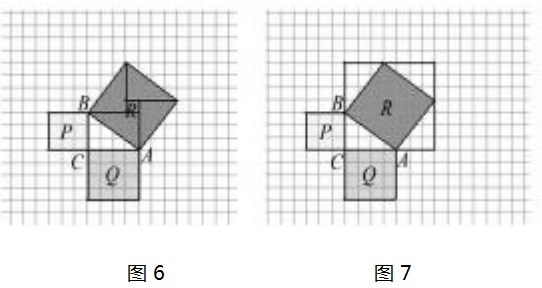
　　在学生展示叙述自己的探究过程和结果后，教师对学生的探究结果给予肯定，并再次进行分析讲解，正方形的面积正是直角三角形的边的平方，进而得出所给直角三角形的两直角边的平方和等于斜边的平方．

　　师2：我们自己找出了所给直角三角形的两直角边的平方和等于斜边的平方，那么这是不是一个特例呢？请大家在所给的方格纸中任意画一个顶点都在格点上的直角三角形，并分别以这个直角三角形的各边为一边向三角形外作正方形，仿照上面的方法计算以斜边为一边的正方形的面积，探究直角三角形三边的关系．

　　由于各个学生所选择的直角三角形的边长不完全相同，而得到的结果却是相同的，即直角三角形的两直角边的平方和等于斜边的平方，这就将前面的特例推向了一般，通过学生成果展示，教师辅助以解释，在学生看来已经验证了前面结论的一般性，但是教师进而追问学生，由于所作图形的边长皆为整数，那么如果边长不是整数，结论是否仍然成立．进而在教师的引导下进入多媒体辅助教学环节，通过几何画板的动态验证，从而初步得到了结论的一般性，教师提示由于没有无限验证，总觉得还有些不太严谨，从而引导学生开展了下面的数学活动．

　　参考文献：

　　[1]中华人民共和国教育部．义务教育数学课程标准(2011年版)[M]．北京：北京师范大学出版社，2011．

　　[2]单中惠．“从做中学”新论[J]．华东师范大学学报(教育科学版)，2002，20(3)：77－82．

　　[3]杨裕前，董林伟．义务教育课程标准实验教科书数学(八年级上册)[M]．南京：江苏科学技术出版社，2007．

　　[4]史中美．“做中学”及其数学课程设计和实施[D]．沈阳：沈阳师范大学，2007．

　　[5]张奠宙，宋乃庆．数学教育概论[M]．北京：高等教育出版社，2004．