摘要：随着《中小学实验教学基本目录（2023年版）》的发布，数学实验这一教学方式逐渐受到师生的关注。该目录明确指出，数学不应仅局限于纸笔运算与推理，还应通过动手操作来深化理解。在动手实践的过程中，学生对数学知识的理解会逐渐深入，对数学的兴趣也会日益浓厚。基于此，文章以数学实验课“折纸——认识黄金三角形”为切入点，探讨了如何在“循理数学”教学理念的指导下，通过数学实验引导学生探寻数学原理、探究问题本质，从而深化对数学的认识。

　　关键词：初中数学；循理数学；黄金三角形；折纸

　　进入初三后，学生的学业负担加重。学困生面对初三的学习内容束手无策，究其根源，往往是因为他们过去对数学重视不足或理解力有所欠缺，未能掌握众多数学基本原理。而学优生及中等偏上的学生则将数学学习简化为刷题训练，满足于解题技巧的掌握，对数学原理与问题本质的探究浅尝辄止。这导致一旦题目形式稍有变化或呈现方式稍显新颖，他们就会陷入困境。

　　破解这一难题的关键在于引领学生步入“循理数学”的殿堂[1]。“循理数学”之“理”，意指基础且核心的概念，尤其强调数学中的逻辑推理。它要求学生在日常学习中主动遵循数学的基本原理与规律，以此作为研究数学、理解数学的基石[2]。

　　一、黄金三角形的定义与性质

　　人教版数学九年级（上册）第二十一章的“阅读与思考”，从正五角星中抽象出了黄金分割数——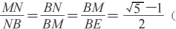（如图1）。黄金分割点的定义：将一条线段分割为两部分，其中较短线段与较长线段的比等于较长线段与整条线段的比，即因此，点N为线段BM的黄金分割点，点M为线段BE的黄金分割点[3]。

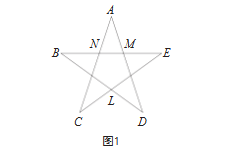
　　在正五角星中，我们还可以抽象出两种黄金三角形——钝角黄金三角形与锐角黄金三角形。钝角黄金三角形（如图1中的△LBE）就是腰和底边的长度比为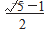的等腰三角形。钝角黄金三角形的顶角为108°,两底角均为36°。锐角黄金三角形（如图1中的△ANM）就是底边与腰的比为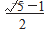的等腰三角形。锐角黄金三角形的顶角为36°,底角为72°,且底角的角平分线将其分为一个锐角黄金三角形与一个钝角黄金三角形。
       总的来说，黄金三角形是短边与长边比为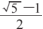的等腰三角形。基于此，笔者设计了一节名为“折纸——认识黄金三角形”的实验课，旨在通过动手操作帮助学生更深刻地理解黄金三角形的定义与性质。

　　二、实验活动

　　（一）用尺规作图在线段上作出黄金分割点

　　学生之前没有构造黄金图形的经验，因此教师在折纸前应为学生搭建支架，先让学生用尺规在线段上作出黄金分割点。

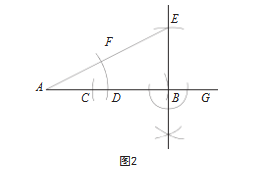
　　黄金分割点的构造难点在于无理数√5，教师可引导学生联想与√5有关的数学知识。学生联想到若直角三角形的两条直角边长度分别为1与2，则斜边长度为√5；矩形的邻边长分别为1与2，则对角线长度为√5。接着，学生完成尺规作图（如图2）。

　　具体的作图方法如下：在射线AG上取线段AD=DB＝1；过点B做射线AG的垂线，在垂线上取线段BE＝AD＝1，连接AE，由勾股定理得，AE=√5；在线段AE上取点F，使得AF＝AD＝1，则EF＝AE－AF=√5－1；在线段AB上，取点C使得BC＝EF=√5－1，则点C为线段AB的黄金分割点。

　　接着，教师引导学生思考：若不改变图2中线段AB与线段BC的长度，但将点C落于AB的延长线上，则点B是否为线段AC的黄金分割点？学生发现，此时点B在线段AC上，使得较短线段与较长线段的比等于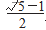，满足黄金分割点的定义。最后，教师引导学生归纳出利用尺规作图做线段的黄金分割点的实验原理。

　　本次实验的重点为通过勾股定理构造长度为√5的线段，再通过尺规作图将长度为√5－1的线段落在线段AB上（或线段AB的延长线上）。通过尺规作图实验，学生获得了在一条线段上构造黄金分割数的实践经验，为后续的折纸实验奠定了坚实基础。

　　（二）折钝角黄金三角形

　　在折纸实验前，教师可让学生尝试用尺规作出黄金三角形，再将作图过程转化为折纸步骤。

　　根据钝角黄金三角形的定义，学生可以构造腰长为√5－1、底边为2的等腰三角形。鉴于最终需要将尺规作图转换为折纸，因此学生可利用邻边长为1和2的矩形的对角线来构造√5。这样，学生仅需将一张正方形纸片对折便可构造出长度为√5的线段。接着，教师让学生在边长为2的正方形纸片上，用尺规作出钝角黄金三角形ABC（如图3）。

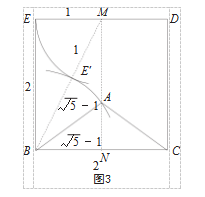
       学生通过分析发现，本次实验的关键在于构造短边AB＝AC=√5－1，长边BC＝2的等腰三角形。因此学生可以归纳出，该实验原理为依据黄金三角形的定义构造。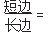

　　（三）折锐角黄金三角形

　　1.通过构造边折叠锐角黄金三角形

　　根据钝角黄金三角形的构造经验，学生本想构造底边为√5－1、腰长为2的等腰三角形，但多番尝试后发现直接构造√5－1的底边存在难度。学生进一步探究发现，可以在构造好的钝角黄金三角形的基础上，完成锐角黄金三角形的构造（如图4）。

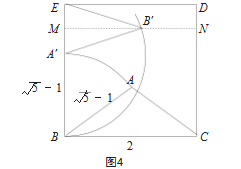
　　在已经折叠出腰AB=√5－1、底BC＝2的钝角黄金三角形ABC的正方形纸片上，以B为圆心，BA为半径作弧交BE于点A'，则BA'＝BA=√5-1。由于正方形纸片的边长BE＝2，此时在线段BE上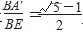，则点A'为线段BE的黄金分割点。根据黄金分割点的定义，线段A'E为锐角黄金三角形的底，A'B的长度为锐角黄金三角形的腰长。依据等腰三角形的顶点位于底边的垂直平分线上的性质，学生可先折出线段A'E的垂直平分线MN，再以A'为圆心、A'B为半径作弧交MN于点B'，则A'B'=A'B，通过等量代换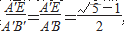，连接B'E，此时等腰三角形A'B'E满足锐角黄金三角形的定义。
       接着，教师引导学生将尺规作图的结果转化为折纸步骤并归纳得出，本次实验通过黄金分割点的定义与等量代换构造底边与腰之比，因此本次实验的原理依然为依据黄金三角形的定义构造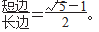        2.通过角度构造锐角黄金三角形

　　学生在探究中发现，在钝角黄金三角形的基础上，还可构造锐角黄金三角形。

　　根据黄金三角形的性质，钝角黄金三角形ABC的底角∠ABC＝36°,∠ACB＝36°（如图5），而锐角黄金三角形的顶角为36°。因此，只需以∠ABC为顶角构造等腰三角形即可。

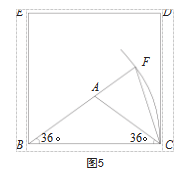
　　在已经折叠出钝角黄金三角形ABC的正方形纸片上，学生以点B为圆心、CB为半径作弧，交线段BA的延长线于点F，则BF＝BC；连接CF，则△BCF为顶角为36°的等腰三角形，即为锐角黄金三角形，且△AFC也为锐角黄金三角形。

　　学生分析归纳出，本次实验的原理为依据锐角黄金三角形的性质构造顶角为36°的等腰三角形。显然，这个实验思路与之前的定义法完全不同，可见，在进行实验活动时，需要理清实验对象的定义与性质，抓住其关键特征，灵活解决问题。

　　（四）实验总结

　　在实验课的最后环节，教师可以引导学生进行总结与拓展。依据黄金分割点与黄金三角形不同的定义与性质，有不同的构造黄金图形的方法。但是，黄金图形的定义均指向黄金分割数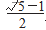，因此黄金图形的实验原理中必定有共通之处。通过总结上述实验原理发现，黄金图形的实验通理为构造黄金分割数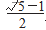。因此可以推测，其他的黄金图形同样可以用这一通理或特殊性质进行构造。为此，教师可以鼓励学生在课后继续探究：能否运用本节课所学的实验经验构造出其他黄金图形？

　　总结环节是对“循理数学”课堂活动的深化。在这一过程中，学生通过归纳实验通理并进行拓展，探寻了构造黄金图形实验活动的本质，深化了对黄金图形的理解[4]。
       三、结束语

　　“循理数学”的实验活动发展了学生的创新能力与应用意识。在实验过程中，学生需要不断尝试、调整思路、改进方法，这种经历能够锻炼他们的问题解决能力，培养他们的创新思维。通过实践，学生能更深入地掌握数学原理，将抽象的理论知识转化为具体的实践经验[5]。这种教学方式不但提升了学生的学习积极性，还让学生感悟到在其他的数学学习活动中也应秉持“循理数学”的精神，深挖数学原理，探寻问题本质，更深刻地认识问题并解决问题。

　　在教学中，教师应践行“循理数学”的教学理念，引导学生在数学学习的过程中探究原理，理清问题本质，这样学生才有可能具备举一反三的能力。通过本次“循理数学”的课堂活动，学生还应思考，在日常生活中同样需践行“循理”精神，探究问题本质，从而更好地解决生活中遇到的问题，让“循理”精神从数学中来，到生活中去。

参考文献

　　[1]李霞.“循理数学:学科育人的理论建构与实践创新[J].福建基础教育研究,2024(10):57-62.

　　[2]陈春凤,何家荣.引领学生循理而思提升数学思辨能力[J].辽宁教育,2025(1):14-17.

　　[3]王可.从黄金三角形到纸折黄金分割点[J].中小学数学,2024(11):36-38.

　　[4]韩东.激趣·循理·启智:指向数学学科育人的基本框架与实践范式[J].小学教学参考,2025(11):1-4.

　　[5]刘强.“双减”背景下初中数学实验课组织教学“三范式”[J].数学学习与研究,2024(20):8-10.