摘要：文章基于研究经验，在概述说理课堂内涵的基础上，结合人教版数学五年级（上册）“平行四边形的面积”的教学内容，系统论述了基于问题驱动的小学数学说理课堂教学策略，提出教师在建构说理课堂的过程中，可以生活问题驱动让学生想说理，以系列问题驱动让学生会说理，以生成性问题驱动让学生有效说理，以迁移性问题驱动让学生多说理，提升说理课堂的建构效果，使学生高效学习数学学科知识，提升综合能力。

　　关键词：小学数学；问题驱动；说理课堂

　　说理课堂可以让小学数学教学更有意义，让学生掌握知识，提高能力，给学生的长远发展带来积极影响。然而，说理课堂需要学生积极参与学习、思考、表达等活动。小学阶段学生的学习动机和学习经验不足，如果教师完全将课堂交给学生，容易出现学生学习效率过低的问题，导致学生不能有逻辑地、准确地表述所学习的知识，甚至产生畏难心理，放弃参与学习活动。对此，教师需要重视引导问题的设计，开展基于问题驱动的小学数学说理课堂教学，在巧妙引导学生学习过程的同时，保障学生自主学习的权利，让学生产生说理兴趣，明确说理方向，提升说理能力，助力学生走出说理课堂的学习困境，推动小学数学教学改革的进程。

　　一、说理课堂的内涵

　　数学说理课堂强调讲“理”。“理”有多种含义，如“数理”，即数学的生成之理。学生在学习数学概念、公式、定理的过程中应“知其然”且“知其所以然”，如能记住“（a＋b）＋c＝a＋（b＋c）”，并能基于具体的应用情境解释“为什么三个数相加时，先把前两个数相加或先把后两个数相加，和不变”。同时，“理”也有“学理”的含义，即学习之道理。教师要让学生理解学习者应主动探索知识，明确学习的过程和方法，敢于质疑，大胆推理，提升批判性思维和探究能力。此外，“理”还有“教理”的含义，即教师应正确认识教育的深层意义，在传授知识的过程中，让学生探索、理解学科知识，而非机械地将知识灌输给学生。说理课堂倡导教师在明教理的基础上，让学生说数理、知学理。

　　二、基于问题驱动的小学数学说理课堂教学策略

　　（一）以生活问题驱动，让学生想说理

　　让学生想说理是建构数学说理课堂的基础。教师可以生活问题为驱动，激活学生说理热情，这有助于营造良好的课堂教学氛围，使学生感知到所学知识与现实生活之间的联系，更好地落实学生核心素养的培养[1]。在具体实践中，教师可先确定生活中与说理课堂教学内容相关的案例，通过讲故事、播放视频、组织课堂表演等方式引入案例，快速吸引学生的注意力，让学生进入教学情境。然后，教师可以与学生展开对话，在对话的过程中使学生发现问题，从而产生有效解决问题、说理的想法。

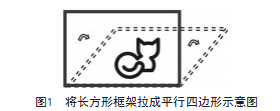
　　例如，在人教版数学五年级（上册）“平行四边形的面积”的教学中，教师需要引导学生探索平行四边形面积的计算公式以及平行四边形与长方形之间的关系。教师可借助视频引入如下生活情境：一名学生在白纸上用金属丝粘出了一只小兔子，并制作了一个长方形框架，将小兔子放在框架里，在框架内部的空余部分贴满了白色小珠子，但他发现白色小珠子不够。此时，他的老师提出了建议“可以将长方形拉成一个平行四边形（如图1），这样使框架内部的面积变小，就解决了小珠子数量不足的问题”。对此，该生表示质疑，教师提出：“我们可以通过实践求出平行四边形的面积，再比较长方形面积和平行四边形面积的大小来解决问题。”在播放视频后，教师可与学生讨论以上情境中的问题。一些学生认为视频中教师提出的方法是科学的；一些学生认为教师提出的想法是不正确的。此时，教师可引导学生通过实践推理后续的视频内容。这样，学生便可产生主动探究的意愿，进而提出核心问题：如何求平行四边形的面积？在这一核心问题的驱动下，学生会进入学习状态，产生说理意愿。

　　（二）以系列问题驱动，让学生会说理

　　系列问题是指教师设计的多个具有关联性的问题。在说理课堂上，教师需要引导学生进行探究，基于探究的过程和结果开展说理活动。然而，部分探究活动相对复杂，一些学生会出现“找不到说理头绪”“难以克服探究时遇到的困难”等情况[2]。对此，教师可以在说理课堂上以系列问题驱动学生思考，让学生在解决系列问题的过程中循序渐进地参与数学学习活动，了解数学学习方法，参与数学探究，并说明探究过程，使学生做到“会说理”。

　　例如，在教授“平行四边形的面积”时，在学生产生探究意愿后，教师可设计系列问题：（1）是否可以通过切割、拼接的方式将平行四边形变成熟悉的图形（如长方形）？（2）如何用字母表示平行四边形面积的计算公式？（3）图中（如图1）的长方形和平行四边形有什么关系？（4）视频中老师的说法是否正确？如何将你的判断分享给视频中的学生？在以上系列问题中，问题（1）能引导学生将平行四边形切割成两个图形，并通过拼接得到新的图形——长方形（如图2），这有助于学生找出探究多边形面积的方法。此后，学生可通过观察，认识到图2中图形①的底和图形②的长相等；图形①的高和图形②的宽相等，根据长方形面积的计算公式归纳出平行四边形面积的计算公式，即“平行四边形的面积＝底×高”。在问题（2）的推动下，学生能以字母更直观地归纳实践成果，即“S＝ah”。而问题（3）可以使学生将探究视野回归生活情境，认识到图1中长方形的长与平行四边形的底相等，长方形的宽大于平行四边形的高，因此长方形的面积大于平行四边形的面积。在问题（4）的驱动下，学生可系统回顾与演示问题（1）～问题（3）的解决过程，参与说理活动，加深对学理的理解。

　　（三）以生成性问题驱动，让学生有效说理

　　生成性问题是指教师在学生探究、表达的过程中临时提出的、非在教学设计环节预设的问题。一些学生在说理课堂上，存在无法把握说理重点、说理内容混乱、说理角度单一等情况，影响了说理效果。对此，教师可以提出生成性问题，借助这些问题驱动学生明晰说理重点、准确组织语言或丰富表达角度，让学生在说理课堂上有效展开说理，提升学生说理的全面性、准确性、科学性等[3]。例如，在讲授“平行四边形的面积”时，教师可关注如下两个提出生成性问题的时机：

　　1.教师提出生成性问题

　　学生在推理平行四边形面积的计算公式时，可能会出现语言表达不严谨、探究方法单一的情况，比如，学生会提出：“可以将平行四边形切割成一个三角形和一个梯形，将这两个图形拼接到一起就可以得到一个长方形，然后根据新长方形的面积求原平行四边形的面积。根据新长方形长、宽和原来平行四边形底、高的关系，可以得出平行四边形面积的计算公式为‘平行四边形的面积＝底×高’。”在学生说理时，教师无须打断学生，但要记录学生存在的不足：（1）语言不够严谨；（2）虽能有意识地通过切割、拼接的方法探究平行四边形面积的计算公式，但受教材的影响，其思维局限于“将平行四边形切割为能够拼接成长方形的三角形和梯形”中。

　　在这种情况下，教师要引导学生调整语言细节，挣脱教材束缚，故可提出生成性问题（1）：是否可以将平行四边形切割成任意形状的三角形和梯形？结合这一问题，学生意识到，要想将平行四边形切割成三角形和梯形，并确保两个图形可以拼接成长方形，应保证两个图形分别为直角三角形和直角梯形。教师继续提出生成性问题（2）：将平行四边形切割为两个直角梯形，是否可以得出同样的平行四边形面积的计算公式？结合该问题，学生可进一步发散思维，通过实践操作、画图、观察，将平行四边形沿着高切割为两个直角梯形，以验证这一方法是否可推理出平行四边形面积的计算公式。

　　结合以上两个生成性问题，学生可以准确说明求平行四边形面积的思路：沿着平行四边形的高将平行四边形切割成一个直角三角形和一个直角梯形，或将平行四边形切割成两个直角梯形。完成切割活动后，将得到的两个图形拼接成长方形，根据原平行四边形的底和高确定拼接出的长方形的长和宽，由此基于长方形面积的计算公式得出平行四边形面积的计算公式为“平行四边形的面积＝底×高”。

　　2.学生补充生成性问题

　　教师在完成基本的教学任务后，可以鼓励学生补充自己未解决的问题。此时，有的学生会提出“在视频情境中，应该将框架拉成什么样的平行四边形？”这样的问题。由此，教师可提供更多信息：“通过测量，视频中的学生发现自己的白色珠子刚好可以铺满边长为6 cm的正方形，而长方形框架的长为9 cm，宽为7 cm。”借助该信息，学生可深入探究，说明自己的探究成果，即“可以将框架拉成底为9 cm、高为4 cm的平行四边形”。

　　这样，教师先引导学生基于探究过程和成果进行说理，在此基础上提出生成性问题，鼓励学生补充生成性问题，可以加深学生对几何图形面积问题的探究方法的理解，取得更理想的学习成效。

　　（四）以迁移性问题驱动，让学生多说理

　　迁移性问题是教师在引导学生获取知识后，迁移运用所学知识做出更多判断、决策等活动的问题。在运用迁移性问题的过程中，教师要引导学生系统、全面地说明解题思路，这有助于学生加深对基础知识的理解。教师在引导学生分享解决迁移问题解题思路、解题成果的同时，也能够丰富学生的说理经验，让学生在多说理的过程中提升对数理、学理的认识[4]。

　　例如，在讲授“平行四边形的面积”时，教师可以在课堂上引入多个迁移问题：（1）图中（如图3）平行四边形的面积之间有什么关系？为什么？（2）图中（如图4）大正方形的面积为9 m2，小正方形的面积为4 m2，求图中阴影部分平行四边形的面积。在这两个迁移问题中，问题（1）有助于学生加深对“平行四边形面积的计算公式”这一重要知识点的认识，确保学生能够在说理的过程中提出“这些平行四边形虽然不完全相同，但因底相等、高相等，因此面积也相等”的结论；问题（2）有助于学生将正方形面积与平行四边形的面积相融合，从而在说理时指出“根据正方形面积的计算公式和已知数据，平行四边形的底与小正方形的边长相等，即2 m，平行四边形的高与大正方形的边长相等，即3 m，根据平行四边形面积的计算公式，可知平行四边形的面积为6 m2”。

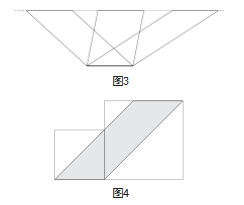
　　教师这样设计迁移性问题能加深学生对已学规则图形面积的计算公式的印象，并能够基于所学说明相关几何问题的计算思路，丰富学生的说理经验[5]。

　　三、结束语

　　总之，小学数学教师要在明确说理课堂内涵的基础上，巧妙通过问题驱动教学，构建说理课堂。在教学实践中，教师可通过生活问题、系列问题、生成性问题和迁移性问题驱动学生在课堂上以积极的态度参与学习活动，掌握学习方法，明确数学知识的探究过程，有效记忆并灵活应用所学，逐步提升说理能力与数学学习效果。

　参考文献

　　[1]王珮珺.数学说理课堂“三问”[J].小学数学教育,2023(24):24-26.

　　[2]黄秀花.聚焦说理能力培育数学素养:小学数学语言能力的培养策略探析[J].数学之友,2023,37(14):6-8.

　　[3]郑民荣.以核心素养为导向的小学数学说理课堂[J].天津教育,2023(24):10-12.

　　[4]朱桂云.基于问题解决的小学数学说理课堂建构策略[J].名师在线(中英文),2023(21):17-19.

　　[5]王荣生,洪安琪.“大概念教学”的三个关键性问题:以语文学科为例[J].全球教育展望,2025,54(3):135-147.