摘要:本文梳理开放性问题的内涵,结合常见的开放性问题类型,讨论其可用情境,指出开放性问题设计应遵循以学生为主体、与单元主题紧密结合、以思维训练为重点的原则,并提出以“基于教学目标定位问题类型—围绕核心素养构建问题—根据教学实际设计拓展问题”为基本路径,灵活开展开放性问题设计与教学的基本策略。

　　关键词:高中数学课堂教学开放性问题设计策略

　　开放性问题教学是培养学生解题能力和锻炼其思维能力的重要方法,但部分教师设计的开放性问题缺乏深度,不利于发挥开放性问题的教学价值。对此,教师应深入了解开放性问题的教学定位、问题形式及对应的功能。

　　一、高中数学课堂教学中开放性问题的设计意义

　　目前,学术界对于开放性问题概念的界定尚不统一,其中狭义的概念是指条件不确定且结果不唯一的问题,广义概念还涵盖了开放性探究中的引导性问题。从教师的角度来看,广义的开放性问题概念更适合作为封闭式问题的补充。由此可以进一步根据开放性问题的形式和辅助教学的功能将其分为四类:一是条件开放性问题,此类问题可以引导学生提出假设,加强其对知识点中关键要素的记忆,还能进一步培养逆向思维;二是结论开放性问题,丰富学生对数学应用或跨学科应用的认知,使其更加熟悉某一数学知识的多种考查方法,培养学生的综合实践能力;三是策略开放性问题,这类问题包含多余且可被利用的条件,可以让学生熟悉某一类问题的多种解决方法,提高学生解决陌生试题、新型现实问题的思维能力;四是综合开放性问题,一般为引导开放性探究的导入型问题,问题中可能不包含具体条件、目标,需要学生自主发现和设计问题、自主调查和收集条件、自主寻找解题方法,这类问题在培养数学抽象、逻辑推理、数学建模、数学分析等核心素养方面有突出优势,可以促进学生跨学科应用能力发展。

　　开放性问题更注重培养学生的思维能力和解决问题的综合能力。《普通高中数学课程标准(2017年版2020年修订)》(以下简称“课标”)在“学业水平考试与高考命题建议”中提出了“应包括开放性问题和探究性问题,重点考查学生思维过程、实践能力和创新意识”。这在一定程度上印证了开放性问题在考查和培养学生的思维能力和综合素质等方面的功能和作用。

　　开放性问题还具备独特的辅助教学功能。例如,开放性问题能激发发散性思维,从而活跃课堂氛围,有助于培养学生兴趣;开放性问题通常没有固定的解题模式、思路,需要学生自主思考和探索,有助于强化学生主体性,培养其自主思维意识;开放性问题不强调必须给出特定结论,可以帮助学生快速完善知识结构,加快知识的内化。因此,教师也可以根据教学需求设计和应用开放性问题,使其更好地服务于课堂教学。

　　二、高中数学课堂教学中开放性问题的设计原则

　　1.以学生为主体

　　开放性问题侧重于“训练”而非“考查”,因此在设计开放性问题及配套教学方案时要尽可能控制“教师干预度”,一方面要减少教师引导环节,另一方面要设计专门引导学生进行发散性思维的策略,以确保学生能够自主发现和解决问题。例如,在“命题与量词”教学中,教师先讲解命题概念,再抛出多个陈述句和疑问句,如“判断其中哪些是真命题、假命题”。这种问题虽然属于结论开放性问题(因为存在非命题语句),但在这种教学流程下学生会自然而然地进行“是否为命题”“是否为真假命题”的思考,难以展开真正的开放式探究。对此,教师需要进一步弱化以知识考查为主的引导,同时增加发散性思维引导,让学生能自主设计问题、讨论总结命题判断规律,探索该知识点相关的试题设计思路。

　　2.与单元主题紧密结合

　　开放性问题一般服务于课堂教学,因此相关问题及教学方案的设计需要围绕单元主题内容来设计,一方面是为了与教材内容、结构更好地搭配,更有效地服务于课堂教学,另一方面是为了与学生发展水平相匹配,确保问题的开放度与学生认知水平有效匹配。例如,在向量定理认知教学中,教师可以引入开放性问题来辅助学生思考。教师设计条件开放性或策略开放性问题,如基于平面向量定理解析平面直角坐标系内某个点的方法,这种开放性问题显然服务于实践能力训练,而非服务于定理解析。教师可以设计“寻找平面向量定理与功向量共线定理的相似点和差异点”等结论开放性问题,使其更好地服务于课堂定理解析教学。

　　3.充分发挥开放性问题的思维训练功能

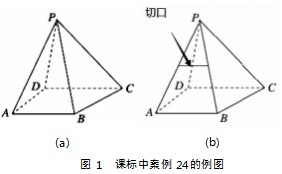
　　开放性问题作为封闭式问题的补充,需要将打破学生思维定式作为基本目标。例如,课标中的案例24提到了四棱锥中平行问题的思维训练策略,如图1(a),一般问题会给出AB//DC的条件,然后设计过程开放性问题,引导学生思考如何将平面内的平行关系转换为立体空间中的平行关系(在△PAB中绘制与AB平行的线,通过其与AB平行进一步证明其与DC平行)。这种开放性问题的思维逻辑是相对固化的,学生容易陷入只运用数学符号和逻辑推理来解决问题的困境。从现实角度来看,这类问题还可以通过空间想象解决,例如,在与AB平行、与四边形ABCD垂直的方向切开四棱锥,起始切口处的线段必然与DC平行,如图1(b)所示。基于这种思维方式,则可将开放性问题设置为“是否可以尝试切开四棱锥,由此在四棱锥的各个面上找出多条与DC平行的线”,以此引导学生进入新的思维角度。

　　三、高中数学课堂教学中开放性问题设计的基本路径

　　为帮助一些不常使用开放性问题的教师更高效地设计有针对性的开放性问题,本文提供如下设计路径:

　　1.定位目标并优化问题类型

　　为了设计出更符合教学需求的问题,教师需要完成以下两步工作:

　　第一,确立与单元教学密切相关的训练目标和主题。首先,开放性问题必须与单元教学主题紧密联系。部分教师会在单元教学中穿插核心素养训练任务,并在此类训练中引入与单元教学内容联系不够紧密的开放性问题,教师在设计开放性问题时需要避免出现这类问题。其次,开放性问题必须与教学目标紧密结合。例如,在一元二次不等式解法思路的教学中,教师可以设计车速与制动距离关系的判断题来引出构建一元二次不等式的综合型开放性问题,也可以基于一元二次不等式的不同解法(因式分解、配方法、变形法等)设计开放性问题。相比而言,后一种问题与单元教学结合更为紧密,更适合采纳。

　　第二,基于教学内容和目标来进一步甄选开放性问题的类型。首先,应基于教学内容特点选择开放性问题的类型。在概念、定理、公式教学中,建议设计条件开放性和过程开放性问题,方便学生从不同角度认识、理解数学知识;在知识的拓展性认知教学中,建议设计过程开放性和结论开放性问题,引导学生讨论,训练学生从不同角度思考和解决问题的能力;在解题能力训练教学中,建议设计条件开放性问题和综合型开放性问题,让学生充分了解各类常见的数学知识应用场景和试题形式。同样,以一元二次不等式教学为例。“以集合表示解集”是重点,那么问题“开放化”设计的中心就要放在如何让学生理解集的意义上。可以设计“随意说一个一元二次方程和一元二次不等式不同之处”“尝试用同一种方法解答x(x-10)>0和(x+1)(x-1)>0”等问题,引导学生自主总结规律,从而深刻认识解集的内涵。

　　2.围绕核心素养构建问题

　　课标中特别提到了要在设计习题时“开发一些具有应用性、开放性、探究性的问题”,并指出这“有助于学生数学学科核心素养的提升”。在保证问题与单元教学主题有效匹配的前提下,教师可按照如下两个步骤筛选问题:

　　第一,根据具体的核心素养培养目标选择问题。高中数学学科核心素养包括数学抽象、逻辑思维、数学建模、直观想象、数学运算和数据分析,教师应根据与单元教学主题融合度较高的核心素养选择最合适的开放性问题。例如,数学抽象的本质是以数学符号归纳事物等对象的规律,所以在大多数的概念认知教学中都可以引入条件开放性问题辅助教学。

　　第二,根据各年级核心素养发展目标选择合适的问题。高中数学中的六类学科核心素养在不同年级的发展标准不同。例如,数学建模素养的一级水

　　平是“掌握数学模型和数学建模基本方法”,二级水平是“在情境中建立简单数学模型”,三级水平是“用多种知识和方法对比较复杂的问题建立数学模型”。因此,教师需要根据学生的实际水平选择匹配的开放性问题。例如,高中函数基本性质的教学对应培养学生的数学抽象、逻辑推理两类核心素养,课标对该部分知识学科核心素养的要求分别为一级(抽象出简单的数学问题)和二级(用多种规则推理并发现简单数学结论)。按照这一标准可以设计两类衔接的开放性问题。例如,在已知一般命题

　　“函数y=f(x)和y=g(x)有着相同的性质P,中y=f(x)·g(x)性质的方法”这种策略开放性问题,再根据逻辑推理素养的培养需要,设计“尝试用同一方法或不同方法分析y=f(x)+g(x)、=”结)开()性、f。(x)/g(x)的性质变化情况，这种结论开放性问题。

　　3.基于教学实际选择拓展引导问题

　　教师应当提前设计拓展引导问题,在教学中根据课堂情况选择性抛出问题,引导学生思考。

　　第一,拓展引导问题的设计思路。与开放性问题不同,拓展引导问题不一定要与原问题的主体相同,但要能起到引导学生发散思维的功能,所以这类问题的本质是提醒学生可以从哪个方向或以何种方法来思考。教师可以通过改变设问方式来引导学生思考,例如,原问题为“随意列出一个通项公式an来证明‘等比数列{an}中,公比大于1,则该数列为递增数列’”,部分学生可能只关注了数列单调性,忽略了首项符号。对于此类情况,教师可以将“随意列出一个”改为“尝试列出多个不同形式”,这样就可以在不做过多指导的情况下引导学生进一步思考,使学生有机会自行发现新的可能性。

　　第二,应用拓展引导问题的时机与方法。拓展引导问题一般只建议在学生自主思考和分析问题效率远低于预期、学生思维能力和应用能力发展效果与开放性问题教学目标出现严重偏差时使用。在抛出拓展引导问题时,教师应以相对自然的方式引导学生思考新问题。例如,在上文提到的等比数列问题调整示例中,教师改变设问方式后不必强制学生直接放弃原本的思路,可以允许学生自由选择两类问题中的一个问题,在此基础上引导学生对比两类问题,让部分学生走完原本的思考过程,然后再结合其他学生分析新问题的思路、方法来进行自我检查和反思,由此发现自身问题。这种引导策略能够弱化“强制性”,保障学生的主体地位,并进一步加强师生、生生沟通效果,从而提高开放性问题的辅学效果。

　　开放性问题有着灵活的课堂教学辅助功能,教师应根据开放性问题的类型和功能、数学课程教学的实际需求、学生知识与应用能力发展水平合理选择问题类型,或调整开放性问题的训练重心。当然,由于开放性问题过于灵活,缺乏一个高度标准化的选材、构题和教学应用参考体系,教师可以结合实践效果持续优化问题式教学框架和构题策略,以更充分发挥开放性问题教学的价值。

　　参考文献

　　[1]陈俊阳.高观点下“构造例子”型开放性问题编制案例—基于Jordan分解定理[J].数学通报,2023,62(1):40-43.

　　[2]王艾琳,张志平.数学思维能力在高中数学教学中的培养[J].科学咨询(教育科研),2023(7):200-202.

　　[3]谢妮.课程知识的开放性与个体的自我关怀—兼与叶波博士商榷[J].湖南师范大学教育科学学报,2019,18(2):112-117.