摘要：数学是一门“结构的科学”，而整合练习注重理解知识结构间的内在联系，是由逐一探索走向整体探究的动态建构。线上线下整合练习能够大大提升了学生学习的效率。本文从大单元视角对线上线下整合练习研发与教学实践进行分析。

　　关键词：整合练习；动态建构；思维发展

　　新课标2022年版提出数学需要让学生“运用数学和其他学科的知识与方法分析问题和解决问题”的目标。为实现这一目标，结合教学学情，线上线下整合练习能够帮助学生主动建构、整理知识点和练习，让学生通过回忆、比较、思考、推理、计算、概括，感受知识结构建构、解构、重构的动态过程，以此促进数学思维的深度发展。由于线上学习本身比较单一，加上概念的抽象化，学生很容易会遗忘。这就需要在线下的整合练习中提升学生的理解和掌握程度。笔者认为，学生应当把握数学概念的逻辑意义，领悟内容反映的思想方法，把握知识间的多元联系，挖掘其蕴含的科学方法、理性精神，让学习由逐一探索走向整体探索。

　　一、宏观设计，支框架

　　本研究结合苏教版小学数学五年级下册第三单元的内容进行研究。《因数和倍数》单元在《数与代数》中包含了“数与运算”和“数量关系”的内容，力求让学生复课之后在一节整合练习中准确掌握学习重点，攻克学习难点，让他们体会到知识之间相互联系、层层递进关系，以建构动态化系统的知识结构。

　　本单元在教材上的教学内容主要分为三大块“因数和倍数，2、5和3的倍数特征（例1-5）”“质数、合数，分解质因数（例6-8）”“公因数和最大公因数，公倍数和最小公倍数（例9-12）”。

　　教学之前教师应当考虑学情。首先，关于本单元学生在此前已经学习了许多自然数的知识，包括整数的认识、整数四则运算，而且在生活中，学生也积累了一定的经验，知道单数双数的意思，能够感受到数字的价值。而本单元的概念学习，是在掌握了之前的学习的基础上，探究非零自然数性质，这部分的概念很多，其内容相当于初等数论的基本内容，是发展学生抽象能力的数学核心素养的关键。其次，学生在家已经将每天对应的课时内容按照进度完成、上传，教师也将每位学生的作业逐一批改，同时学生还完成了订正的任务，且已经掌握了基础的数学知识内容。每天晚上教师会进行线上答疑，答疑的时候既会帮助学生回顾知识点内容，也会评讲学生的日常作业，部分难题在线上已经得到解决。虽然参与了两次的直播课，但是学生居家学习的习惯很难把控，学习的效果参差不齐。

　　根据以上的分析以及一节课的时长，笔者对教学内容结构稍作了一些调整，认识和找一个数的因数和倍数，2、3、5的倍数特征；（根据2的倍数分）奇数、偶数（和与积的奇偶性）；（根据因数的个数分）质数、合数，质因数、分解质因数；公因数和最大公因数、公倍数和最小公倍数。

　　基于以上考虑，根据2022版的数学新课标，力求数学知识之间的联系，在设计练习之前笔者有如下的思考：第一题了解学情，中间几题帮助学生巩固和攻克学习重难点，最后一题的综合题整合多个知识点。在进行大单元设计的时候考虑全单元的内容、学生的学情、课时的设置等，这样教师既能掌握教学全局，学生也能在其中感受到建立的知识框架，让学生既看到整个森林，又可以从一棵树开始，从最基础学习走向更高层次学习、巩固、提高，强化头脑中相关的知识点和知识体系，从而达到见树又见林。

　　二、“点”动成线，增知识

　　线上线下整合练习的设计需要涵盖所有知识点，巩固学生对每一课时概念的理解，从而充实对该单元多个知识点的掌握。简单地讲，就是让学生在原有线上学习的基础上进行再学习、再研究，力求让每一位学生都能掌握每个知识内容的细枝末节，提升相关知识的思维能力。

　　（一）在刻意练习中强化知识

　　这里的刻意练习是指在练习的时候应该有一定的要求，即练习要有一定的目标、挑战性、反馈和评价。学生在线上已经练习过书本上的题目，想有所发展，就需要编写有效的练习。笔者借鉴已有的题目，在编写练习的时候进行必要的深度改编。有的练习就扩充一下内容，例如练习的第一题，就是根据苏教版这一单元整理与练习的第4题进行扩充，使得难度加强、知识面广泛一点，围绕“算式7×9=63，认识和找一个数的因数和倍数”进行巩固，提问：“根据这道算式说说谁是谁的因数、谁是谁的倍数。”“63的因数有哪些？7的倍数有哪些？9的倍数有哪些？”“你是怎样找到的呢？因数和倍数的特征有哪些？”这样学生通过一道算式，就能够巩固认识和找一个数的因数和倍数的知识和方法——“因数和倍数都是指两个数之间的关系”“一个数的因数最小是1，最大是本身，个数是有限个；一个数的倍数最小是本身，没有最大的倍数，个数是无限个”。通过一道算式可使学生理解数与数之间的关系。

　　有的练习来自笔者研发，这样的改编为日常教学提供了丰富的数学学习材料，让学生接触更多元的学习材料，加深对数学知识价值的认识，从而更准确把握数学知识的本质。例如，在“和与积的奇偶性”教学中，“判断结果是奇数还是偶数并说说你的想法。19+17+15+13……+7+5+3+1（偶数个奇数相加的和是偶数）21+19+17+15+13……+7+5+3+1（奇数个奇数相加的和是奇数）21×19×17×15×……×7×5×3×1（奇数）20×19×18×17×……×4×3×2×1（偶数）（几个乘数中，只要有一个偶数，积一定是偶数）”。通过授课，笔者发现学生对于“和与积的奇偶性”的学习比较薄弱，对于存在的规律一知半解，只知道两个数相加相乘的规律，对于多个数的运算还处于计算、推理得到结果的过程中，不知道判断和的奇偶性只需要看奇数的个数，积的奇偶性只要看有没有偶数，因而不能熟练地掌握知识要领。

　　每一题都是选取了学生平时容易记错概念的数，比如，设计了猜电话号码的环节，根据每个数字具有的特征设计的条件让学生回答，这道题既是整个单元涉及到的知识点以及特殊数的整合，又在提醒学生有些数很特别。学生在推理的过程中经历逻辑推理和有序的分析，这样的复习不仅仅让学生知道结果，更知道结果得到的顺序、过程，感受到与生活的联系。

　　在学习的过程中，学生达到的目标不仅仅是知道答案，更要知道答案背后涵盖的内容和能力。比如，在找一个数的因数和倍数的时候，“63的因数有哪些？7的倍数有哪些？9的倍数有哪些？你是怎样找到的呢？特征什么？”学生能够有意识地找到相对应的答案，但是在想“怎么找”的过程中便是有序思考，在考虑“有什么特征”的过程中更是思维的进阶。

　　单元整合课中每一题的练习都包含了多个知识点，学生在有目标、有挑战性练习的过程中反复强化对知识点的理解。这样不同题型和目标的练习，都可以让学生循序渐进地感受到知识的实用性，让每一位学生都能够接触到这一单元不同知识点的深度内涵。

　　（二）在问题链中深度学习

　　在分析和解决每个练习的时候，笔者都设置了一系列的问题，从而形成问题链，这样的问题链在不断的互动和对话当中让学习达成深度学习。教师可以有意在每道练习背后都设计出有关联的问题，如第四个练习围绕算式7×30=210，对“质数、合数、质因数的含义以及分解质因数”进行巩固。通过“按因数的个数分的话，非零自然数可以怎么分？（质数、合数和1）什么叫质数，什么叫合数，1呢？50以内的质数有哪些？哪个数较特殊？为什么？（2既是偶数又是质数）根据算式说一说：哪个数是哪个数的质因数？什么数可以分解质因数？（合数）乐乐每天放学后都做一些练习题，一次，他连续三天做题的数量是三个连续的自然数，并且乘积是210。乐乐这三天分别做了多少道题？（分解质因数）”等设计许多提问和追问，这些提问和追问由学生线上的错题汇集而来，并且其中的知识点也比较多、比较细碎，虽然是一道算式，学生却能巩固数学概念，掌握易错的知识点，体会到知识运用于实际的价值。

　　这样有意地提问和追问，让学生增加知识之间的联系，加深对知识的理解、掌握，进而将知识一步一步推入更高层次的探索。这样一来，学生的数学学习就超越了具体知识和技能深入到思维的层面，由具体的数学方法和策略过渡到一般性的思维策略与思维品质的提升。

　　三、连“线”成体，拓思维

　　根据2022版新课标，数学学科尤其是“数与代数”部分强调了整体性和一致性，学生心中如果没有知识体系框架，就难以形成核心素养。实践表明，不少学生掌握的数学知识是零乱的、分散的、彼此孤立的。所以，促进学生认知结构整体性、概括性和结构性尤为重要。而以“线”成体简单地讲就是在动态的学习过程中让学生了解到整个知识体系与学习目标的全貌。

　　（一）知识点整理，培养全局观念，建立结构认识

　　认知心理学认为，认知结构具有整体性和概括性，并且整体性和概括性越强，就越有利于学习的保持和迁移，所以笔者鼓励学生对知识点的学习。

　　整理单元的知识点就能很好地让学生将单元知识梳理了一遍，在梳理的过程中也就自然绘制了一幅“结构全景图”，而且在展示的时候，学生通过比较也会发现，用思维导图可以直接找出知识之间的联系，而利用不同颜色绘制，会更加清晰地区别出每一部分的知识点。从制作到评价培养了学生思维的整体性、条理性，建立了结构认知。

　　这一举措会发现学生有知识点遗漏，但能够进行相互补充。所以学生在汇报的时候，通过相互补充能够将整个单元的知识点梳理全面。而且从学生整理的知识点不难发现，学生的整理很精彩，有一一列举、树状图、思维导图等形式，还有用不同颜色的笔进行区别整理的。有的学生还有好题推荐，这样的题目也可以在活动课的时候让学生进行分享和评价，从而促使学生的学习成为一个主动的过程。教学既应当让学生注意到每一节课的知识点的学习，也要让学生了解大单元、大主题下的逻辑关系，树立全局观。

　　（二）动态学习，建构知识形成过程的结构

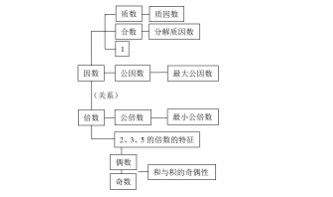
　　整合练习中教师应当有意引导学生发现每个知识之间的联系，让学生在习得数学知识的概念、定义、解决数学问题的方法的同时，感受数学知识内在的统一性，进行动态建构。例如，在认识和找一个数的因数和倍数之后，教师们先巩固了2、3、5的倍数特征，然后通过是不是2的倍数，将非零自然数分为奇数和偶数，而与之相关的就是和与积的奇偶性，而一个非零自然数按是不是2的倍数分为奇数和偶数，按因数的个数又可以分为质数、偶数和1，再以此延伸。这样的连续的线性学习，既让知识之间的联系可视化，又可以让学生对知识之间的内在关联建立了清晰的印象，建构了完善的知识网络。

　　一节课下来，在一次次的延伸下，就动态地呈现了完整的知识结构（如上图）。所以，在整合练习中不应只拘泥于教材中的层次和脉络，而要努力探索、不断发现，让数学学习在动态建构的过程中，实现数学核心素养的关联生长。

　　四、结语

　　想要有行之有效的线上线下整合练习，就要意识到练习既不是对已学知识的简单重复，也不是单纯的查漏补缺，而是通过练习，对原有知识、经验进行调整、改造、归纳、整理，构建知识体系。方法就是根据已有学情，利用大单元视角，在练习的编排和研发上注重知识的动态结构性和探索性，在此基础上进行更高层次的再学习，以达到巩固提高、融会贯通的目的，促进数学思维的深度发展。因此，数与代数部分的整合练习应该将知识由厚到薄，又由薄到厚地进行，力求让学生与知识之间建立起联系，对数学进行动态的结构化思考，从而使得知识“点”动成“线”、“线”动成“体”。