摘要：文章主要论述了如何挖掘“医学统计学”思政元素，包括在浩瀚的医学统计学史中寻找科技名人的光辉事迹，发挥示范引领作用；在抽象概念中融入求真务实、诚信分析的理念；从正态分布特征中深刻体会社会发展不同阶段政策或举措的重要内涵；等等。

　　关键词：“医学统计学”教学；思政元素；人文素养

　　医学是依托自然科学、融入社会科学、体现人文科学的一门复杂的学科。医学教育不仅肩负着对医学本科生进行专业知识和专业技能培养的任务，还承担了他们人文素养、职业道德、思想素质等方面培养的重要社会责任[1]。习近平总书记在全国高校思想政治工作会议上明确指出，“其他各门课都要守好一段渠、种好责任田，使各类课程与思想政治理论课同向同行，形成协同效应”，从而要“把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面”[2]。由于医学教育实施的特殊性和医学知识传播的时效性，以基于对主动需求医学知识的快速获取、批判鉴别、整理与分析，从而做出医学或卫生决策为基本素质的医学统计素养，将成为每个医学本科生都应当具备的基本能力之一，这也是其未来从事医学工作的重要条件和必需的基本素质[3-4]。

　　作为医学本科阶段开设的一门影响广泛、层次贯通、以科研思维训练为重的专业基础课，“医学统计学”在培养卓越医生计划过程中，必然成为重要的必修课之一[5-6]。在思政教学融入的大背景下，由于授课人数遍及整个医学本科生群体，因此思政元素融入这门课的相关内容是非常重要的。对于一门学习难度较高、数理场景为主、思维模式抽象的课程来说，思政元素想要自然融入并非易事，故教师要深入挖掘思政元素，将其与各知识点对接，以便开好“医学统计学”思政课程[7]。因此，本文从“医学统计学”涵盖的知识点出发，从思政教学内容及要求考虑，深入地挖掘思政元素，从六个典型案例着手，系统阐述，以便在后续授课过程中真正做到“医学统计学”专业知识与思政元素点对点融合。

　　一、在浩瀚的医学统计学史中寻找科技名人的光辉事迹，发挥示范引领作用

　　医学统计学史的介绍是“医学统计学”绪论章节的重要内容之一。“医学统计学”绪论章节从历史发展的角度对医学统计学相关事件、理论和方法的产生、形成及发展进行了系统的梳理，但在历史人物部分大多以国外的统计学家的介绍为主，如卡尔·皮尔逊和罗纳德·艾尔默·费舍尔，很少涉及国内对医学统计学发展做出重要贡献的历史人物。在思政元素融入专业课的大背景下，笔者将原第四军医大学医学统计学家、教育学家郭祖超教授作为医学统计学发展史中重要的历史人物进行了翔实的介绍，以促使学生在“医学统计学”教学过程中感受到我国医学统计学发展史中光辉灿烂的一页。郭祖超教授是我国著名的医学统计学家、军队卫生统计学家和医学教育家。其在20世纪40年代最早在中国系统地介绍医学统计学方法，是中国医学统计学的开拓者和缔造者，为推动中国医学科学的发展做出了重要的贡献。20世纪50年代初，为适应中国人民解放军在现代化战争中卫生工作的需要，他着手创立军队卫生统计学，是第一位运用现代统计学方法搜集和分析中国人民解放军卫生工作统计资料的组织者、指导者和实施者，为中国培养了一大批优秀的高级专业人才。郭祖超教授一生始终保持着劳动人民朴实无华的品质，毕生安于清苦的教书生涯，以培养后生为己任，乐而不怠；始终忠于党和人民的伟大事业；始终如一地践行着“非淡泊无以明志，非宁静无以致远”的伟大科学抱负。他在不同人生阶段用心启迪着一代又一代从事医学统计学钻研工作的后辈学者，其言语中无不体现着以天下教育为己任的崇高品质。比如，“得天下之英才而教育之，乐也”，表现出一种桃李满天下的自豪感；“严谨的科学作风是靠平时养成的”，表现出一种严谨求实的科学态度；“先当学生，后当先生”，表现出一种谦虚有佳的工作和生活态度；“科学工作者是相信真理的，而真理只有一条—有了共产党，才有新中国”，流露着坚持真理，爱国爱党的崇高信念；“只要我能为人民做点有益的工作，在医学上起个螺丝钉的作用，这就是我一生最大的愉快”，则是一种自发地为人民服务的社会担当。郭祖超教授的这些言行无不折射出感人深厚的先进事迹、浓郁至深的家国情怀、高尚无私的爱国热情及为科学献身的崇高精神，能润物细无声地感染学生，使学生在理解和掌握医学统计学发展史的过程中产生心灵共鸣。

　　二、在抽象概念中融入求真务实、诚信分析的理念

　　误差理论是统计学理论得以建立的重要基础。因此，对误差的概念及分类的理解决定了统计学思想的理解深度和广度。在医学统计学中，误差是指观测值与真实值、样本统计量与总体参数之间的差别[8]。而根据误差的性质和来源，主要分为系统误差和随机误差。系统误差是由一些固定因素产生的，如仪器未进行归零校正、标准试剂校准不好、测量者获取测量值有固定方向的偏差等，以及在临床试验或观察研究中研究对象选择不当、医生对疗效标准掌握不准等。简言之，就是人为因素导致的观测值与真实值的偏差。而随机误差又分为随机测量误差和抽样误差。其中，随机测量误差是测量仪器虽然按操作要求校准或归零，但对同一测量对象多次测量结果并不完全相同，是随机产生的误差；另一种随机误差则是抽样误差，这种误差是因为生物个体的不同而产生的，故从总体中随机抽取一个样本进行研究，所得样本统计量与相应的总体参数往往并不相同，即由于抽样而引起的样本统计量与总体参数间的差别。由此可见，系统误差可以通过操作者的规范性要求、质量控制、认真的科研态度得到彻底的消除和避免，同时随机测量误差主要通过仪器精度的提高便能得到很大程度的改善；而对于抽样误差，在人群研究中，只要没有得到总体，通过样本特征来估计总体的特征就会存在这种误差。当然，这种误差也不是不能得到有效的改善，一个很简单的办法就是让样本更“像”总体，可以采取的措施包括以下两种：①样本量足够大；②随机抽取样本，使样本对总体的代表性大大增强。而这样的条件实际上在现实的研究中很容易满足。在现实中，有些研究者虽然采取了严格的质量控制措施，也得到了很好的样本，但通过分析，并没有得到统计学上显著性的差异。此时，为了发表文章或得到预期的有统计学显著性的差异，可能就会随机篡改数据，这样实际上是把抽样误差变成了系统误差，尽管得到了统计学上的显著性差异，但得到的统计量与真实的统计量产生了很大的偏差，估计的总体参数自然也是不准的。因此，要想保证科学研究的质量，不仅要通过严格的质量控制得到有代表性的样本，并通过随机误差理论得到科学的结论，还要通过求真务实、尊重科学、诚实守信的科学态度维护科学的结论，即教师可以通过引导学生对这些抽象概念进行辨析，从而使学生领悟求真务实、尊重科学、诚实守信的科学态度的重要性，并将其内化于心、外化于行。

　　三、从正态分布特征中深刻体会社会发展不同阶段政策或举措的重要内涵

　　正态分布是最常见、最重要的连续型随机变量分布，该分布由法国数学家德·莫阿弗尔于1733年提出。德国数学家高斯在研究误差理论时建立了此分布。正态分布理论为数理统计学的建立奠定了重要的理论基础，一些重要的概念，如小概率、小概率事件等的取值依据都是从正态分布规律中产生的。正态分布曲线形态呈钟形，两头低、中间高，左右对称。其形态如图1所示。

　　在数学上，正态分布曲线的函数表达式中有两个重要的参数：位置参数μ和形态参数σ。正态分布曲线下的面积分布有一定的规律。正态分布曲线下所夹的面积恒等于100%；区间μ±σ的面积为68.27%，区间μ±1.96σ的面积为95.00%，区间μ±2.58σ的面积为99.00%。具体如图2所示。

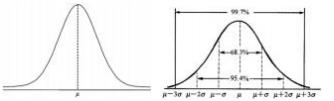
　　当随机变量X分布在区间μ±1.96σ或区间μ±2.58σ时，正态分布的尾部概率分别是5%(0.05)或1%(0.01)，这里的0.05或0.01就是小概率取值的理论依据。从整体上看正态分布可以发现，其中规中矩，不偏不倚。与其他连续性分布不同，当呈现正态分布时，数据表现出了“和谐”分布状态。人的收入状况是决定社会稳定的重要因素，在我国社会主义发展进程中，人的收入稳步提高，与经济水平相协调，这是人民实现共同富裕的外在表现，而社会共同富裕则是构建和谐社会的本质要求。在特定的历史时期，为了加快实现共同富裕的步伐，我国采取了一部分地区、一部分人可以先富起来，再带动和帮助其他地区、其他的人，逐步达到共同富裕。在这个政策的执行前期，地区间人们的收入可能呈现正态分布，95%的人的收入位于μ±1.96σ的区间内，如果所有人的收入都按统一步伐前行，此时整个社会人们收入的峰值位置向右移动的速度会非常缓慢，再加上一些收入调节政策的不平衡，久而久之，峰值甚至会向左偏移，提示贫困人口过大；执行“一部分地区、一部分人可以先富起来，带动和帮助其他地区、其他的人，逐步达到共同富裕”政策后，由于许多地区人们收入水平提升迅速，有可能会出现峰值向右严重偏移，提示两极分化严重。而这两种情况都不利于构建和谐社会。当后一种情况出现时，就要消除贫困，让分布左侧的“长尾巴”消失，转成分布均值较近的左侧的一分子，从而使整个社会人们的收入水平分布继续保持和谐。因此，2015年12月8日，《人民日报》刊登了中共中央、国务院通过的《关于打赢脱贫攻坚战的决定》[9]。2020年，我国取得了脱贫攻坚战的最后胜利，实现了全民奔小康，国家从此进入了小康社会，其意义是非常重大的。小康社会是和谐社会不同阶段的表现形式。从正态分布的角度来看小康社会的实现，可以发现我国人民的平均收入水平较以往已经得到了空前的提高，且维持了整个社会人民的收入为正态分布的和谐景象。而“一部分地区、一部分人可以先富起来，带动和帮助其他地区、其他的人们，逐步达到共同富裕”只是通过暂时的偏态，实现均值大幅提升后的正态而采取的阶段性的策略，而达到共同富裕，维护和谐社会才是国家最终的目标。通过对脱贫致富奔小康的讲解，教师可以使学生理解正态分布的特征和曲线下的面积，掌握专业知识的同时，感受到我国脱贫攻坚全民奔小康的社会意义，深刻理解走向共同富裕的历史必然性。

　　四、从统计推断中科学认识和理解两类错误

　　两类错误是统计学假设检验中普遍存在的两种错误。如果真实情况与检验假设H0一致，由于抽样误差，使得计算的检验统计量的值落到拒绝域内，导致本来接受H0的结论而得出拒绝H0的结论，从而所犯的错误，称为I类错误，其概率用α表示；如果真实情况与检验假设H0不一致，检验统计量的值却落到了接受域内，本来应该拒绝H0却接受了H0，所犯的错误称为II类错误，其概率用β表示。统计推断与真实情况的联合概率分布如表1所示。

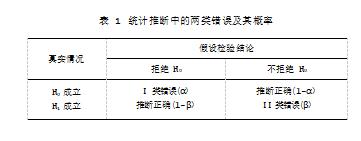
　　在科学研究中，统计学方法的根本任务是通过样本特征来推断总体特征，由于获得样本时，抽样误差总是存在，此时两类错误不可避免，而且α增加时，β会减小。因此一般是基于一次抽样获得的样本来推断总体特征的。在一次统计推断中，I类错误发生率是小概率，但并不等于发生概率为0，因此，统计推断的结论并不是西部素质教育2022年10月第8卷第20期100%的正确。为了减少这种错误，可通过多次抽样、多次检验得到一致的结论，以保证科学结论的可靠性，即检验结果的可重复性。对此，教师可引导学生了解现实生活中一些事件的发生也是如此，如新冠肺炎的核酸检测由于受到检测试剂或检测方法的影响，一次检验的结果与实际感染状态并不一定是100%的吻合，对于疫情流行地，卫生行政部门总会采用多次检测来消除一次检测不准带来的影响，以便最大限度地发现感染者并采取严格的隔离措施，从而避免由于检测出现的问题而导致潜在疫情向健康人群传播的风险。基于此，学生就会明白，要自觉遵守疫情防控政策，积极参与新冠肺炎的核酸检测，如此在保障自身安全的同时，也能避免因一次检测不确定而带来传播其他人群的风险。通过讲解，学生会从内心深处感受到疫情处置中自觉遵守疫情防控要求，积极参与新冠核酸检测对防止病毒的传播和保障人民健康的重要意义。

　　五、从统计学方法比对中引发思政共性思考

　　在单变量的统计推断中，按总体分布已知与未知通常分为两类检验方法：参数检验方法和非参数检验方法。参数检验方法是指在总体分布已知的前提下对分布位置进行的假设检验，如Z检验、t检验、方差分析等；而非参数检验方法是指在总体分布未知或不依赖总体分布类型，而对总体分布的位置直接进行假设检验的方法，如威尔科克森符号秩和检验。威尔科克森符号秩和检验方法是非参数检验中最常见、使用频率最高的一种检验方法。对于t检验来说，其要求样本服从正态分布，因为t检验的理论基础是t分布，而t分布是从正态分布中衍

　　生出来的抽样分布，所以t检验也是基于正态分布理论框架下的参数检验方法，其根本仍然是用正态分布的规律来解决假设检验的问题。当然，正态分布的均数和中位数是重叠的。但有时候原始数据不一定满足正态分布，出现正偏态分布(或右偏态分布)或负偏态分布(左偏态分布)，此时原始数据就不能直接用正态分布理论的方法(如Z检验、t检验、方差分析等)对这类数据的均值进行假设检验了，因为正态分布规律是建立在对称性基础上的，此时对称性被打破了。秩和检验方法就是对这类数据位置直接进行检验的一类统计推断方法。不管分布如何，总能通过秩变换转化为秩分布，而秩分布从形态来看，无论是正态还是偏态，总是左右对称。从秩和检验和Z检验的数据分布入手进行比较，可以发现，秩分布形态左右对称，但秩和检验方法较Z检验方法应对的原始数据在分布上出现了很大的偏差。既然原始数据分布不对称，那么就可以通过秩变换后秩分布变成正态分布，接着就可以利用正态分布的理论来解决秩数据的问题。也就是说，一组数据无论原始数据如何，它们秩分布形态是较固定的，总是对称分布或正态分布，故正态分布的规律就可以应用于秩分布上。也可以这样理解，秩分布相同时，原始数据分布有可能不同。这样利用“同”解决“不同”，可以为解决不同分布数据的假设检验问题提供新的思路，如图3所示。

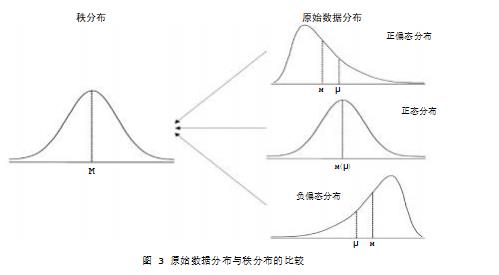
　　党和国家于20世纪50年代提出了“一国两制”的构想，用于解决香港、澳门和台湾问题。1997年7月1日和1999年12月20日，香港和澳门分别回到了祖国的怀抱，这标志着“一国两制”的思想由理论变为现实。“一国两制”的思想也在一定程度上体现了中国共产党在解决国家统一问题上坚持了策略灵活性和原则坚定性的辩证统一，即用“同”来解决“不同”的问题。这与少数民族区域自治政策一样，同一个国家，但用不一样的民族政策形式解决实际问题。基于教师的讲解，学生可通过香港、澳门回归的“一国两制”思想中用“同”来解决“不同”的问题的例子，从而延伸理解非参数检验方法与参数检验方法秩分布的“同”来解决原始数据分布特征的“不同”问题，这样不但可以掌握非参数检验方法的理论知识，而且能不由自主地对国家统一、民族伟大复兴产生无比的自豪感，进而从内心深处对国强民富，实现祖国的完全统一充满了憧憬和向往。

　　六、从唯物辩证法中理解统计思想及赋值

　　唯物辩证法是自然界、人类社会和思维发展的一般规律，是辩证法思想发展的高级形态，如对立统一规律。在医学统计学中，统计学模型是用来解决复杂问题的重要手段，如一般线性回归、多元线性回归、Logistic回归和Cox比例风险回归等。这些模型在处理数据之前总要对数据进行赋值，一方面应符合统计软件可计算的要求，另一方面要使分析结果具有专业上的可解释性。比如，自变量X赋值为男性=1，女性=0，结局变量高血压Y赋值为高血压=1，无高血压=0。其中，无论是自变量X还是结局变量Y的两个取值，都是对立的，这便构建了一对矛盾。1是我们关心的取值，用模型分析数据最后结果可以理解为自变量X=1与X=0相比对结局变量Y=1的效应。当自变量X赋值发生改变，如变成男性=0，女性=1，此时，效应值也发生了改变，若两者有关系，具体的关系与所采用的模型相关。因此，在赋值的时候，一定要清楚自己关心的效应是变量的哪个类，如关心男性相对于女性而言Y=1的效应，要按男性=1，女性=0赋值，如果关心的是女性相对于男性而言Y的效应，X应该赋值为女性=1，男性=0。当然，Y变量的赋值发生改变的时候，也会发生与X变量变化类似的情形。变量值中赋为0的变量通常被认为是参考值，与参照物有相同的作用。当然，一些软件在设定参考值时的方法不同，也会影响到最后读取的效应值的差别，如SPSS、SAS软件在许多模块的参考值设定中并不相同。如果运用对立统一理论来理解赋值的全过程，在发生不同软件相同方法输出不同结果时，就需要考虑到参考值设定的问题。通过讲解，学生利用唯物辩证法中对立统一规律的思想深刻地理解了统计学的思想和变量赋值的过程，从而彻底地明白了变量赋值在统计分析结果中的重要性。

　　总之，医学类专业课程思政建设已经走上了医学教育的议事日程，同时教师通过思政元素的融入，能真正地使学生在润物细无声中接受知识、提升能力和培养价值观。医学统计学涉及的思政元素是很多的，但并不是很直接，总是隐藏在知识点背后，需要深入且细致的挖掘，这与其他部分医学课或通识课内容浅显易懂，思政元素易于融入的特点并不太一致，主要原因是医学统计学是从数理的角度来解释医学数据的规律，进而准确地使用统计学方法揭示数据背后的规律性来为专业研究服务的，因此相关知识点本来就很抽象，内容大多以理性思维的训练为主。例如，贝叶斯统计也是医学统计学方法的一类，涉及诸多公式，学生理解起来并不容易，所以教师将其与思政结合时必须要在授课前进行有效准备[10]。另外，不同的“医学统计学”授课教师对知识点的理解不同，挖掘的思政元素也不同。本文主要是对“医学统计学”授课中六个相关知识点思政元素融入的考虑，这一方面丰富了“医学统计学”融入思政元素的案例，另一方面也为丰富特定的教学内容提供了重要的参考依据。

      参考文献：

　　[1]董斌,武艳,吴萍,等.课程思政视域下医学生思政素养现状及影响因素研究[J].医学教育管理,2020,6(3):278-284.

　　[2]习近平在全国高校思想政治工作会议上强调:把思想政治工作贯穿教育教学全过程开创我国高等教育事业发展新局面[N].人民日报,2016-12-09(1).

　　[3]姚烨,李梁.医学类专业课程思政建设的思路与构想:以复旦大学上海医学院“卫生统计学”课程为例[J].甘肃高师学报,2021(2):112-116.

　　[4]许茜,刘志臻,俞向梅,等.健康大数据时代下的医学统计素养培养:“医学统计学”课程思政实践初探[J].教育教学论坛,2021,3(12):57-60.

　　[5]蔡志奇,陈燕忠.推进药医工融合培养跨学科应用型医药人才[J].医学教育研究与实践,2020,28(1):17-20.

　　[6]伍亚舟,易东,张彦琦,等.案例教学法在医学统计学教学中的应用[J].基础医学教育,2011,13(7):635-638.

　　[7]申英英,刘耕,乔素娟,等.思政教育融入医学统计学教学探析[J].中国轻工教育,2019(2):45-49.

　　[8]李康,贺佳.医学统计学[M].7版.北京:人民卫生出版社,2018.

　　[9]关于打赢脱贫攻坚战的决定[N].人民日报,2015-12-08(24).

　　[10]陈耀庚,孙博文.以贝叶斯公式为案例的医学统计学课程思政教学设计[J].医学教育研究与实践,2021(5):781-784.