摘 要：基于新课程改革要求重视学生思维能力培养的大背景，高中数学教师应重视数列试题的教学。文章从讲 述数列章节的重要性出发，针对学生的学习特征，详尽分析了高中阶段数学各类数列试题的具体解题方法与技 巧，以提高学生的数学思维能力。

　　关键词： 高中数学;数列试题;解题方法;解题技巧

　　数列指依据一定顺序进行排列的一列数。数列中 的数被称为这个数列的项，排首位的为首项，排第二 位的为第二项……以此类推，排在第 n 位的数，就被 称为第 n 项，一般会用“an ”表示。在高中数学教学中， 数列是学生习得知识、锻炼思维能力的重点内容。又 因为数列与函数和不等式间的紧密关联，数列这一章 节的试题题型相对复杂。学生在解此类试题时也会产 生无法解答或是不能轻易解答的困扰。结合新课程改 革背景下高中数学课堂需转变学生解题思维、增强学 生学习意识、推进学生核心素养发展的要求，高中数 学教师不仅要重视数列这一章节内容的教学，还要格 外关注数列试题解题方法与技巧的教学。只有这样， 学 生才能在解题的过程中掌握与数列相关的解题方法与 技巧，精确且迅速地解答数列问题。

　　一、数列章节的基础内容及重视试题方法与技巧研讨 的重要性

　　(一)数列章节的基础知识与内容

　　通过对新高考题型的分析与解答，可以明确数列 这一数学内容在其中的重要地位。又因为数列内容的 复杂性，高考时的数列试题难度都会比较大。所以， 数 列是高中数学教师公认的重点和难点 [1]。

　　以苏教版数学必修 5 第 12 章“数列”为例。本章 主要讲述了“数列的概念”“等差数列”和“等比数列” 以及两者的整合运用。虽然本章的教学内容并不繁 杂，但数列内容中有着极为丰富的数学思想和方法。

　　特别是数列求通项与和，解题方法不仅多，且需要解题者拥有灵活的思维。对于教师来说，不仅要通过对 数列各类解题方法的细致归类，拓展学生的解题思 路，还要依靠对典型例题的选取，使学生逐步形成数 列试题解题意识。

　　(二)掌握高中数学数列试题解题技巧与方法的 必要性

　　基于新课程改革的教学要求，数列层面的教学不 应只停留在概念讲述和理论阐释方面，还应让学生依 赖一定的方法和技巧，对数列试题进行深层次的探讨 和研究，以使学生在理解能力逐步提升的基础上，强 化自身综合应用能力与解题能力 [2]。

　　新课程改革对高中数学试题解题技巧与方法教学 也提出了相应的要求，新高考制度下的试题也展现出 了符合课程改革要求的内容，如数列与函数的融合、 数列与方程的融合、数列与圆的融合等一系列问题。 这些问题的变换不是为了增添难度，而是为了促进学 生数学思想上的融合。当学生学会了针对这类问题的 解题方法，其整体知识框架也会得到完善。

　　(三)在高中数学教学过程中重视数列试题解题 技巧与方法教学的价值彰显

　　1. 有助于学生数学学科素养的提升

　　无论是概念上的数列试题考查，还是数列通项公 式的试题考查，学生在解题时，都会用到各式各样的 解题方法，如累乘法、累加法、倒序相加法等。这些 解题方法都在某种程度上展现了有魅力的数学思想。 而包裹在这些方法中的思想核心，除连接了与函数相关的数学内容，还与导数存在着密切的关联 [3]。由此， 教师在结合数列试题讲解解题技巧时，就会借助数列 与其他数学知识间的连接，发散学生的数学思维。学生 也会在思维的发散之下，提高自身数学学科核心素养。

　　2. 有助于拓宽学生的知识面，便于学生构建完善 的思维体系

　　在解数列试题的过程中，高中生一般只会单一地 应用数列公式或是概念性质，进行针对数列问题的求 解。而分析近几年的高考试题可知，数列试题的呈现 并不单一。为此，学生若能够通过知识的连接进行解 答，部分数列题目也会变得相对简单。而这个过程要 求学生拥有联系各方数学知识的能力。

　　由此可见，教师重视数列试题解题技巧与方法的 教学，明显有助于拓宽学生的知识面，帮助学生形成 综合化的数学思维体系 [4]。

　　3. 有助于学生解题思维及意识的形成

　　高中的数学教育离不开思想、方法及应用实践的 教育。高中数学教师不能再沿用以往传统的教学方式 进行知识讲解及解题教学。数列作为高三的教学内 容，本身就具备一定的复杂性，加之与其他知识的关 联，更让一些数列问题难度加大。假设学生连基础的 知识内容都没有牢固掌握，他们在学习或是解题的过 程中，就会出现不想学、不想解的想法。为让学生形 成熟练性的解题思维和意识，高中数学教师要重视数 列试题解题方法与技巧的教学，继而通过问题中的知 识引导和探究，促进学生数学学科核心素养的发展。

　　二、数列试题的解题方法及技巧研讨

　　(一)结合数列的基础概念，解答简易化数列问题

　　基础概念虽然核心在基础，但也是学生解答相关 问题的关键，会对学生的解答思维产生一定的影响。 初中阶段的数学学习通常不会关联至数列内容， 因 此，学生都是在进入高中阶段以后，才开始对数列问 题有一定的认知的。这时，为发展学生思维能力、提 高学生解题能力，教师就要重视夯实学生知识基础，丰 富学生知识储备 [5]。

　　例题 1：当前有一等差数列 {bn }，已知 b4 =4. S10 =55.试求出 S4 为多少。

　　分析：依据题意可知，此题考查的是学生对等差 数列概念的掌握。所以，在解答此题的过程中，教师 可引导学生融合等差数列的概念进行解题，使学生通 过对通项公式的灵活应用求出答案。

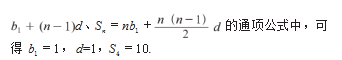
　　(二)基于绘图方法的应用，解答填空式数列问题

　　在解答数列问题的过程中，绘图方法也是学生需 要掌握的一种解题技巧，而绘制的前提在于，解题者 要懂得融合题干中的已知数量及关系，展开图形绘 制，然后再依照直观性的图像来探究题干问题中所含 的数量关系和核心规律。这样，复杂的数列问题才会 变得相对简单。

　　(三)立足数列试题的性质，解答非常规数列问题

　　数学性质作为数列部分知识学习进程中的重要内 容，能够有效协助学生提高数列解题效率。为此，高 中数学教师在结合例题讲述解答方法时，就要重视数 列性质层面的知识传授，且要教授学生怎样结合数列 性质来解答一些非常规的数列问题。这样，学生的数 学思维和解答数列问题的能力才可以得到提升。

　　例题 3：已知 {bn } 为等比数列，其中 n 是正整数， 且 b1b7=36.试求出 b3b5 +b6b2 为多少。

　　分析：在解答这一等比数列问题时，假设解题者 应用比较符合常用规则的解题策略，即依照等比数列 的通项公式进行问题解答，在解答 b3b5 +b6b2 为多少 时，就容易出现不正确的答案。但如果借由等比数列 的性质进行问题解答，就能够快速得到此题的答案。

　　分析：这两道题分别从等差数列和等比数列的角 度，向学生提出问题。学生在解答此类通项公式及前 n 项和时，就要重视对公式的掌握，比如对等差数列的 通项公式和前 n 项和公式、等比数列的通项公式和前 n 项和公式的掌握，都可让学生在解答通项公式、前 n 项和时，迅速通过公式给出相应的答案。

　　(五)关联函数层面的思想，解答复杂化数列问题

　　在数学思想中，函数思想有其独特的思想价值，不 仅能够将繁杂的问题简易化，还能够有效完善学生的 解题思维。教师在讲述关于数列问题的解题方法时， 就 可关联函数层面的思想，解答一些复杂化的数列问 题，并以此为核心，促进学生数学学科核心素养的 提升。

　　例题 5：已知函数y =f (x) 为 R 上单调递增的奇函 数，数列 {an } 为等差数列，a3>0.则f (a1)+f (a3)+f (a5) 的值为( )。

　　A. 恒为正数 B. 恒为负数

　　C. 恒为 0 D. 可正可负

　　(六)重视方程思想的结合，解答目的性数列问题

　　在高中时期数学学习的过程中，方程思想和函数 思想十分相似，都是学生应该掌握且应用在解题时的 核心数学思想。在解答部分数列问题时，假设能够相 对灵活地对方程思想进行运用，那繁复的数列问题也 会被简化。关于方程思想在数列问题中的定义，实则 就是在求解的过程中，依据系列化数列公式来搭建对 应的方程组，之后借助方程组的解答形式，获取正确 答案。

　　(七)融合数列问题举一反三，解答联合性数列 问题

　　为提高学生对一类数列问题的解答熟练度，教师 可融合数列问题，列出举一反三的问题，以此提高学 生解答联合性数列问题的能力。

　　例题 7：已知一列数 2.8.26.80. …，按此规

　　三、结束语

　　综上所述，在高中数学教学过程中，数列是十分 重要的一类题型。由于数列试题对应解答方法所呈现 出的内涵较为丰富，学生不仅可以在解题的过程中掌 握一定的函数思想和方程思想，还能够通过解题巩固 自身对数列公式、概念及性质的应用。但在实际了解、 观察或是阅读解答数列问题时，学生一定要认真解读 数列问题上的题干内容，这样才能够基于题干内容选取 适当的求解方法，进而提升求解数列问题的能力。

参考文献

　　[1] 许美金.高中数学数列试题的解题方法与技巧研 究[J].当代家庭教育,2021(2):119-120.

　　[2] 赵向杰.高中数学数列试题的解题方法与技巧[J].数 理天地(高中版),2022(10):18-20.

　　[3] 刘克江.浅析高中数学数列试题的解题方法与技 巧[J].课程教育研究,2020(19):142.

　　[4] 崔丽雯.针对高中数学数列试题解题方法技巧的分 析[J].试题与研究,2019(18):154.

　　[5] 杨荣智.探讨高中数学数列试题的解题方法与技 巧[J].高考,2019(8):231.