摘要：本篇围绕着对数学中的递归思维，对绘画的影响进行局部的一种探讨。整体分为两节，第一节主要介绍递归与分形的关系，引入一些相对经典的分形图像，并列举一些艺术家在此类分形影响下进行的绘画创作，第二节主要讨论通过计算在递归运算下的迭代生成的分形图像与混沌之间的关系，再进而列举一些艺术家在此灵感下创作的相关作品。

　　关键词：递归思维；递归运算与分形

　　数学是什么？我们可以认为数学是人们最核心、最抽象的知识源泉，是宇宙的语言，数学的本质就是简化。伽利略说“大自然这本书是用数学语言写成的”。数学的整个架构，是人们在寻求万物规律时人为定义出来的，它将人们所掌握的知识，以一种极度严密的逻辑关系连接起来。我们生活中接触到的几乎所有学科，都是在数学的指导下实现和演进的。

　　对艺术而言，数学的价值显而易见，在描绘现实世界问题中，我们对自然规律运作得益于数学的强大逻辑体系，数学能成为哲学家与艺术家的灵感源泉，似乎也就在意料之内了。毕竟，早在文艺复兴时期，艺术家同样是最优秀的实用数学家，而且在16世纪前，他们也是最博学、最多才多艺的理论数学家[1]。只要数学依然在影响着这些世界，那么艺术家便会情不自禁地去接受和表达这种感受。

　　数学的体系过于庞大，其中主要门类就有几十种，世界上可能也有成百上千的数学艺术家，因此我对数学的探讨和艺术家的了解都是不全面的，进而我想围绕着我着重研究的课题方向，对数学中的递归思维对绘画的影响进行局部的一个探讨。

　　人类社会存在两种循环方式，一种是迭代，一种是递归。迭代的方式很早就被掌握了，例如十进制就是以10为周期进行的迭代，再例如12个刻度就可以表现每天的时间。看起来人类的社会就是基于迭代的方式运行，但随着链式反应的发现，人们发现了另外一种计算方式，就是递归运算。

　　例如印度数学家拉马努金这个式子√（1+2√（1+3√（1+4√…)))=3，如果我们将根号中及其内部的内容看成一个函数，则会发现这个函数在不断地调用其自身，于是它会产生一种类似核链一样的无限过程，这就是一种递归循环。

　　著名的斐波那契数列就是一种递归循环方式，如果用一种表达式表示即f（n）=f（n-2）+f（n-1），如果将等式拆解下去，则会发现f（n）=f（n-4）+f（n-3）+f（n-2）ⅆ,这个式子中的f（x）其在不断地调用其自身，最终趋向于一个无限过程，因此人们总是觉得黄金分割比例是最美的，其原因就在其内部就包含了一种无限循环的递归运算方式。

　　计算机圈的彼得·多伊奇就曾说过“迭代是人类的思维方式，而递归是神的思维方式。”因为递归思维超出了人类的惯性思考方式，对人类思维提出了巨大的挑战，就像核链的反应就是通过递归循环并发出巨大的能量，由此来看递归是一种极其强大的计算方式。

　　谈论到递归算法，那就离不开基于该运算方法生成的图形。1967年曼德勃罗特在美国《科学》杂志上发表了题为《英国的海岸线有多长？》的著名论文，这样一个看似简单的问题却引起了一个近50年来数学界最具影响的新理论——分形几何学①。

　　分形最早由本德华曼德勃罗在1973年命名，其具有以非整数维形式充填空间的形态特征，通过计算机的递归运算生成的一个整体与局部具有高度自相似的图形。分形表现了一种简单性与复杂性的关系，复杂的系统可以基于简单的原则。

　　基于分形的理论，衍生出了分形信息、分形设计、分形艺术等。

　　一、递归运算下的分形图像

　　1883年，德国数学家康托尔更正传统意义上完备稠密的观念，利用递归过程创建了一个三分点集，名为康托尔集②。在一条线段上进行三等分，去掉中间1/3，再对余下下段执行其过程，可得出一个整体与局部具有自相似性结构的图案。从“康托尔集”（图1-1）产生过程中可以看出，递归算法也具有自相似性。

　　1916年数学家谢尔宾斯基定义了康托尔集的二维版本，即谢尔宾斯基地毯，具体操作如下：

　　将一个实心正方形划分为的9个小正方形，去掉中间的一个小正方形，再对余下小正方形重复这一操作得到谢尔宾斯基地毯。（图1-2）

　　把正方体每个面分成9个正方体，将正方体每一面的中间的正方体去掉，再把最中心的正方体也去掉，以此方法重复无穷多次以后，便得到门格海绵。（图1-3）

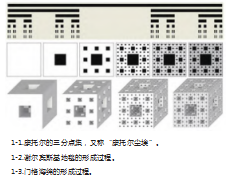
　　递归思维结合计算机生成图像，为艺术家创作提供了灵感：

　　醉心研究于分形的钱德勒与伯克联手完成的一幅作品，是用伯克的计算机画出海绵后，再用合成的方式贴上小朋友的图案。（图2-1）

　　法国艺术家西尔维·顿莫耶尔2010年创作的数码印刷作品《门格海绵上的反射》（图2-2），将一个迭代一次的黄橙色的门格海绵置于视觉中心，背景以蓝色调为主，法国艺术家让·克劳德·梅纳德基于谢尔宾斯基地毯的原理，遵循其布局，在树脂玻璃上创作的纹样《过量》[2]。（图2-3）。

　　同样的方式，数学家谢尔宾斯1915年发现一个由3^n个边长为1/2^n个三角形组成，但内部却留下了许多被掏空的空隙，操作步骤如下：

　　先作一个正三角形，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，用这一方法无限连续地做下去，则可得到谢尔宾斯基三角。类似的分形图案，13世纪已经出现在意大利阿纳尼教堂的卡斯莫迪马赛克上和卡斯美丁圣玛利亚的罗马大教堂中殿的地毯上。

　　将二维谢尔宾斯三角扩展到三维，变成四面体，即将一个正四面体不停地拆分，就是著名的谢尔宾斯基四面体。谢尔宾斯基三角形的面积越趋近于零，而它的周长越趋近于无限大。

　　类似的还有科赫曲线③,其模拟了英国的海岸线，指出随着测量精度的增加而不断增长直至无限，这一有悖于常理的结论，1904年科赫利利用递归方法创作出来，并在他的论文中给出了严格的证明，科赫称其为“朴素的直观”，是一个1.26维图形。（a^D=b D=1og4/10g3）将三个科赫曲线进行拼接，则可以得到“科赫雪花”，数学艺术家法绍尔也使用大小不一的科赫雪花完成一幅图像。

　　分形图案的镶嵌更为五彩缤纷，展示了艺术如何与数学科学的融合。其中最著名的是数字艺术家利用龙分形图形结构，将其遵照黄金螺旋线的轨迹进行平铺的镶嵌，斑驳的色彩尤其引人关注。

　　二、混沌的图像

　　分形的历史与计算机和混沌理论的发展具有密切的联系。在早期，数学家只是对数学好奇，因为从中可以展示有限的空间和无限的交融[3]，随着计算机运算效率的提高，相对简单的公式人们可以在计算机上演算出高度复杂的图形，著名的“曼德勃罗特集”④就是这一效应最复杂最著名的例子。（图3-1）

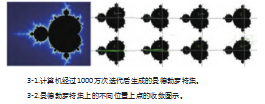
　　曼德勃罗特集是数学家曼德勃罗在1975年发现的一个点集，集合也被称为“上帝的指纹”。这个点集出自一简单的公式：Zn+1=(Zn)^2+C（Z^2=（a+bi）^2），对于非线性递归公式，利用计算机计算后，使得无限递归运算后的结果能保持收敛性的复数c（复数形式是形如a+bi的数字）的点集合。

　　在每个不同大小的圆中，收敛的点与分岔个数都遵循一定的规律。如图所示，横向坐标轴上的圆中的点遵循为2n的等比数列，不在横向轴上的圆的点则按每个圆面积大小遵循斐波那契亚数列（面积越小收敛的点数越多），每个小圆上分岔数与圆内部收敛的点数相同，同样遵循斐波那契亚数列。（图3-2）

　　无限放大后的图像，局部与整体具有自相似性，只要计算的次数足够多，不管把图形放大多少倍，都能显示出精细的局部，这些局部既与整体不同，但又具有某种相似的地方，具有无穷无尽的细节和自相似性。因为这些局部的图形很像海马的卷曲尾巴，数学家将其命名为海马谷。

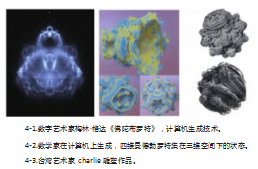
　　根据曼德勃罗特集所提供的灵感，数字艺术家梅林·格达利用一种技术，记录所有收敛与非收敛的点，通过在点上施加权重来表现颜色深浅，再经过后期降噪调整出一幅图像，因其外形类似于一尊大佛，所以命名为《佛陀布罗特》。（图4-1）

　　三维的曼德勃罗特集是不存在的，但可以在四维空间中进行表现，数学家2010年用四元数和双复数来构造，它是曼德勃罗集在三维的等价物。（图4-2）台湾数字艺术家也利用曼德勃罗球原理制作出的雕塑作品。（图4-3）

　　将Zn+1=(Zn)^2+C换成Zn+1=(Zn)^n+C，这里的n是任意实数，当改变n值的时候，图像也会发生不同的变化，生成类似于曼德博罗特集一样的分形图案。例如，当n=3时，类似于眼睛一样的形状，当n=7时，类似于花瓣一样的形状。

　　由此可知，随着指数的变化，可以生成无数类似于曼德博罗特集一样的分形图像。这就是递归运算的魅力之处，因此彼得•多维奇说道：“迭代是人类的思维方式，而递归是神的思维方式”。

　　说到曼德勃罗特集，还离不开一个集合“朱莉亚集”⑤。事实上朱莉亚集比曼德勃罗特集出现还要早几十年，但因那个时代并未计算机，受制于当时的算力，所以并未受到重视。朱莉亚集与曼德勃罗特集类似，也是由Zn+1=Zn^2+C公式迭代所得。与曼德勃罗集相反，将复数c取固定值，取某一z值，可以得到序列，将使其不扩散的z值的集合称为朱利亚集合，理论上朱莉亚集有无数种不同的图案，而且两者在结构上具有紧密的联系。

　　朱莉亚集的结构也给予很多艺术家灵感，珠宝艺术家马克•纽森就是基于朱莉亚集分形概念为宝诗龙设计了一系列的高级珠宝。

　　除了艺术家外，还有很多数学家通过利用递归运算的方式生成各式各样的分形图像。数学家约翰·威廉·斯多弗发现了一种分形曲线，称为“斯多弗曲线”。他制作了一系列由这种曲线构成的彩色海报，这些海报在20世纪60年代风靡全球，斯多弗曲线也被广泛应用于各种艺术品（绘画、雕塑、建筑）中，为人们带来无限的美和创造灵感。

　　德国艺术家佩特根也是受到曼德勃罗的影响，于1985年德国慕尼黑主办了一场名为《混沌之美》的展览，展出了很多利用计算机生成的分形图像与大自然中的分形模式照片。在德国展览后又在世界进行巡展，在世界各地引起了巨大的反响。

　　三、结语

　　复杂性的系统基于简单的原则，世界是一个看似的无序的混沌系统，其运行就好似数学中的递归运算，人们通过利用递归方式生成的分形可以恰当的解释复杂的混沌现象。就像非线性系统的混沌是复杂无序的，看似在不可理喻、无规律的外表下，它的内在结构却遵循着分形一样的秩序，使得混乱的现象却可以通过简洁的方式而掌握。

　　分形是天使，其图像呈现出的秩序与美感背后深刻的逻辑为艺术家提供了丰富的素材参考，其背后严谨的逻辑体系也为艺术家提供了深刻的理论指导。利用递归运算生成的分形颠覆了人们对传统事物的认识，给艺术家带来了全新创作灵感。

　　这样的图像只是通过一些简单的运算进行一次次的递归便可生成，将数学思想融入绘画创作之中，也让当代艺术家看到了绘画创作的更多可能性。

　　注释：

　　①江南.《分形简史》.北京电子工业出版社,2020.第1章1.1分形历史概览(1-4).

　　②江南.《分形简史》.北京电子工业出版社,2020.第1章3.3康托尔集的产生过程(23-25).

　　③詹姆斯·格雷克.《混沌:开创一门新的科学》.楼伟珊译,人民邮电出版社,2021.第4章大自然的一种几何学(96-98).

　　④詹姆斯·格雷克.《混沌:开创一门新的科学》.楼伟珊译,人民邮电出版社,2021.第8章混沌的图像(230-245).

　　⑤江南.《分形简史》.北京电子工业出版社,2020.第5章5.2.2朱莉亚集的产生过程(42-44).

　　参考文献：

　　[1]琳恩·盖姆.《数学与艺术》[M].李永学译,天津科学技术出版社,2023(276-277).

　　[2]莫里斯·克莱因:《方文化中的数学》[M].张祖贵译,复旦大学出版社,2004(476-477).

　　[3]大卫·韦德:《完美的对称》[M].何三宁译,湖南科学技术出版社,2024(034).