摘要：为有序分析电网中日益丰富的谐波检测数据，提出了一种基于灰色模型的电力谐波相关性分析方法，用以分析被监测线路的谐波频域变化趋势、季节波动特性、以及不同被监测线路的谐波相关性。首先，利用FFT方法分析各被监测线路电压谐波数据的频域变化趋势；然后，引入灰色模型求取电压谐波的趋势值，并根据趋势值和原始数据计算季节波动特性；最后，分析各线路电压谐波趋势值、季节指数之间的相关性，辨识非谐波源线路中受谐波源影响较大的线路。通过实际算例分析，验证了所设计的方法可对海量电压谐波数据进行有效地挖掘，分析得到与谐波源线路相关性较强的线路，为谐波治理提供有效的数据支持和决策依据，具有较高的工程可行性，适用范围广。

　　关键词：谐波,灰色模型,季节指数,相关性

　　0引言

　　随着大量非线性负荷的投入，其所产生的谐波电流不断注入电网，并在各母线上产生谐波电压，影响电网中敏感设备的正常工作，造成谐波污染。大多数非谐波源线路受谐波源线路中谐波的干扰影响，影响程度具有一定的规律性，但也带有一定随机性，同时还具有长期性和隐蔽性的特点[1]。目前，电网中装设有大量的智能监测终端，可获取海量的谐波监测数据[2],这些数据具有明显的大数据的特征[3]。但即使已有大量的谐波监测数据，也往往不容易察觉或辨识谐波变化的趋势、季节波动特性以及不同被监测线路的谐波相关性。如何科学地对电网谐波大数据进行深入挖掘，寻找谐波变化规律并确定在电气或潮流上有连接的其他线路与谐波源线路的相关性，实现非谐波源线路中受谐波源影响较大的线路辨识，从而科学地对谐波进行监管与治理，是实际工作中的一个亟待解决的难题。

　　目前，谐波分析研究主要关注的是谐波测量、谐波源定位以及谐波污染责任的划分等[4-8],很少对已测得的电压谐波大数据进行二次挖掘研究，以发现这些数据的内部规律及数据之间的联系。面对越来越多的电力系统监测数据，已有许多学者都进行过数据挖掘研究[2,9-17],但专门对谐波数据进行相关性分析的并不多见，文献[10]中采用线性回归来进行求取电压谐波的趋势值，该方法的优点是可以在一定程度上反映谐波的线性变化趋势；缺点是回归模型的拟合需要大量的数据才能保证模型的准确性，而且不能反映谐波的非线性变化，甚至可能会导致结果出现错误。

　　本文把谐波数据看作一组时间序列[18],拟利用灰色模型来计算谐波的趋势值，该模型建模所需数据量少，所得趋势值能体现数据中非线性的变化规律。由于时间序列存在趋势和季节性等特点，故本文首先选取灰色模型求取时间序列的趋势值，获取数据的趋势规律；然后，利用历史数据与趋势值求取谐波数据时间序列中的季节波动特性，即季节指数（无量纲指标），此时，将谐波数据分为趋势值和季节指数两部分进行分析，能更清晰地发现谐波数据的变化规律；最后，利用相关性分析法，分别求取各线路之间趋势值和季节指数的相关性。该方法不仅可以掌握被测路线自身的变化规律，同时也可以发现谐波源线路与非谐波源线路之间的相关性，深入分析谐波数据的变化规律和联系，为谐波管理与治理提供有力的决策依据。

　　1谐波时间序列

　　一组按时间顺序排列的数据构成了一个时间序列，这个时间序列可分解为4个不同的组成成分：趋势值、循环周期项、季节指数和随机项［18］。按时间顺序排序的谐波数据可认为是一组时间序列。

　　一组时间序列的持续时间可以是1y或1y以上，并且任何时间序列模型通常被表示为一个加法模型或一个乘法模型，即在t时刻的时间序列值指定为：

　　Yt=Tt+Ct+St+R t（1）

　　Yt=Tt·Ct·St·Rt（2）

　　这两种模型表明了时间序列的4个因素，趋势值（Tt），循环周期项（Ct），季节指数（St）和随机项（R t）的共同影响。以上两种模型可以通过对数变换相互转化，故只需讨论其中一种情况，本文选取的是乘法模型。

　　该模型中，趋势值为一单调增或单调减的趋势，无周期性或波动性。循环周期项的变化呈波浪形状，通常长达数年。季节指数与循环周期项类似，其持续通常在1 a内，且循环发生。随机项是指在时间序列中并非由以上所述的任何其他变化造成的不规则变化。实际中，随机项可能对确定谐波水平带来不确定因素。由于尚未能充分把握掌握这些随机项的规律，各标准更倾向于选取诸如95%或99%的概率大值（简称CP95值、CP99值）进行分析，尽量降低随机变化对确定谐波水平的影响［10］，本文选取电压总谐波畸变率（VTHD）的CP95值。

      2算法设计

　　本文所设计的算法拟采用灰色GM（1，1）模型［19］求取谐波电压的变化趋势。首先对原始数据进行FFT分析；之后通过数据累加生成，使原始数据形成符合指数分布规律的生成序列，从而建立统一的微分方程，求得数据的趋势值；然后根据趋势值和谐波电压的原始数据求得季节指数；最后利用相关性分析法求取各谐波电压数据之间的相关性。以下分别对GM（1，1）模型、季节指数和相关性分析进行详细介绍，并给出本文所设计算法的步骤。

　　2.1 GM（1，1）模型

　　设有原始数据序列：

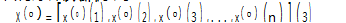
　　对其作一阶累加生成，得到：

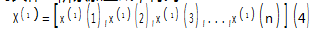
　　式中，k=1，2，…，n。

　　构造一阶线性微分方程为：

　　利用最小二乘法求解参数a，u得：

　　其中：

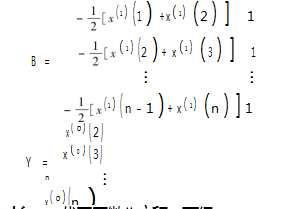
　　将a、u代回原微分方程，可得：e-ak+k=0，1，2，…，n-1（7）

　　累减还原得到：当k=t时，x′（0）（k+1）对应时间序列中的趋势值Tt。

　　2.2季节指数

　　循环周期项和季节指数之间的根本区别是所研究的时间长短不同。此外，季节的变化被认为是可预见的，

　　而循环周期项的影响常要一年以上甚至几年才会显示出来，故本文不考虑循环周期项的影响。假设谐波的时间序列数据不包含循环周期项，则可以通过以下公式来表示：Yt=Tt·St·Rt（9）

　　当k=t时，x′（0）（k+1）对应时间序列中的趋势值Tt，则季节指数St和随机项Rt可由下式求得：=St·Rt（10）

　　为了降低随机分量对季节指数的影响，季节指数可由下式求出：

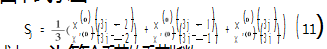
　　式中：Sj为第j个季节的季节指数，j=1,2,3,4;x(0)为谐波的CP95值，对应于Yt;x′(0)为趋势值，对应于Tt。

　　2.3相关性分析方法

　　为了找到不同数据之间的趋势的关联程度，采用回归分析中的相关系数ρ,对不同数据之间（假设为x,y之间，其公式如下。(12)

　　式中：COV(x,y)为x和y的协方差；σx、σy分别为x和y的标准差。

　　2.4算法步骤

　　本文算法流程如图1所示。

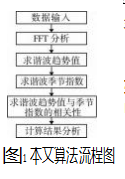
　　(1)数据输入，输入的数据为待检测线路VTHD的历史值；

　　(2)对谐波时间序列进行FFT分析，根据频谱图判断谐波的波动性；

　　(3)利用灰色模型求出谐波时间序列的趋势值Tt;

　　(4)利用式(11)求出谐波时间序列的季节指数St;

　　(5)利用式(12)求出谐波时间序列各趋势值Tt及各季节指数St之间的相关性。

　　(6)根据相关性的计算结果，分析各线路变化规律的联系。

　　本算法利用灰色模型求取的趋势项反映了谐波数据的变化趋势，季节指数则反映了谐波数据的季节波动性，结合两者便可掌握被测线路自身的谐波变化规律。分别求取各线路之间的趋势项和季节指数的相关性，可以得到各线路之间的联系。因此，本算法实现了对电压谐波大数据的更深入更全面的挖掘。

　　3实例分析

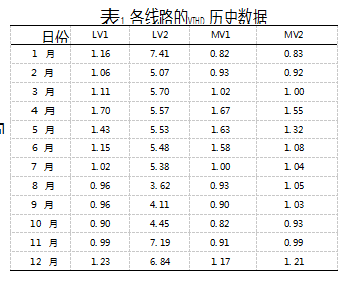
　　本文以某供电局110 kV变电站电压谐波数据为例进行分析。数据来自该变电站负荷类型相似的两台11010 kV主变S1、S2的两10 kV低压(LV1、LV2)线路和两中压110 kV(MV1、MV2)线路的的电压畸变率(VTHD)数据，表1为各线路VTHD历史数据。由表可知，两台主变的低压侧的VTHD数据差异性较大，其中，LV1的VTHD符合国家标准的限值[20],而LV2的VTHD数据超标，可以当作谐波源线路。同一变电站内负荷类型相似的线路，出现如此大的差异，因此该数据具有一定的代表性，很有必要深入分析谐波源线路与其他线路的内在联系。

　　3.1 FFT分析

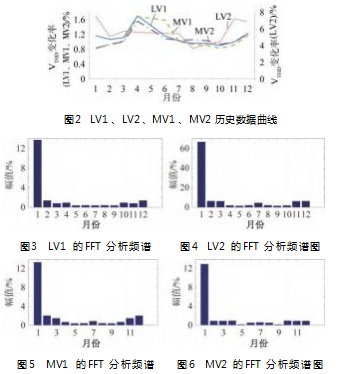
　　为了更清晰地分析各线路VTHD的变化规律，利用FFT观察各线路VTHD在频域下的变化规律。图2为4条线路VTHD的历史数据曲线图，图3~6分别为线路LV1、LV2、MV1和MV2的VTHD的FFT分析频谱图。

　　可以看出，LV1、MV1、MV3无论是从历史数据，还是从频谱图来看，其数据都存在一定的变化规律，即在1~4月、10~12月，VTHD呈现上升趋势，4~10月VTHD呈现下降趋势，且在4月达到最大值。而LV2中历史数据不符合上述变化规律。由FFT分析可知，这些数据的变化在频域下都呈现出某一周期性变化，而这一周期性变化由于是在一年内发生的，可以认为这是由于季节性波动造成的，因此除了寻找这些历史数据的变化趋势外，还应该寻找因此在谐波时间序列中的季节性指数。

　　3.2相关性分析

　　(1)利用灰色模型计算各线路VTHD的趋势值，并计算季节指数。趋势值如表2所示。利用式(10)求得各条线路的季节指数S1~S4,如表3所示。

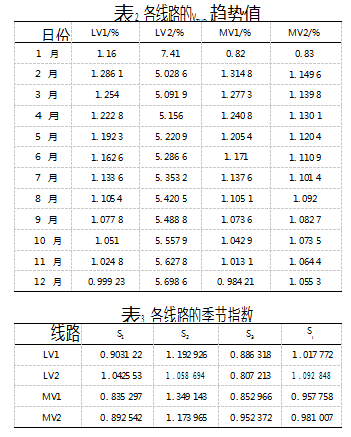
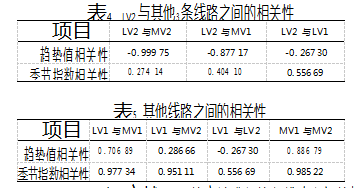
　　利用式(11)计算得出，各线路VTHD趋势值的相关性和各线路的季节指数的相关性如表4~5所示。

　　(2)利用文献[10]的方法求得的各线路之间的相关性如表6~7所示。

　　3.3计算结果分析

　　(1)由相关性分析结果可知，文献[10]的算法中，由于采用了线性回归模型，使理论趋势值的增长方式为线性增长，没有体现趋势值的非线性变化，使趋势值的相关性只出现完全正相关或负相关，从而导致分析结果存在缺陷，甚至误判。而引入灰色模型可以在一定程度上克服该缺点。进一步分析可以发现，在季节指数的相关性中，两种算法的相关性分析表明当两线路的季节指数存在强相关性时（如LV1和MV1、LV1和MV2、MV1和MV2),两者分析结果接近一致，也证明引入灰色算法可很好地反映季节波动性。

　　(2)由表4可知谐波超标线路LV2与中压线路MV1、MV2的趋势值均具有强负相关性，表明当LV2谐波超标时，谐波变化趋势与中压线路相反；LV2与低压线路LV1的趋势值呈弱负相关性，表明LV1的谐波变化趋势与谐波源线路LV2之间并没有存在很强的联系。另外，LV2的季节指数与其他3条线路之间的相关性均不是很强，甚至与MV2为弱相关性，表明当谐波超标时，谐波源线路的季节波动性不仅与环境、气候、负荷类型等有关，还与某些因素（如设备老化，滤波器安装与投切）等有关，从而导致LV2的谐波季节波动性出现异常。

　　(3)由表5可知，非谐波源线路LV1的趋势值与MV1呈强正相关性，而与LV2、MV2呈弱相关性，表明当谐波合格时，同一台变压器的高低压侧之间的谐波变化趋势相同，而与另一台变压器没有太大的相关性。值得注意的是，LV1与其他线路之间的季节指数相关性和LV2的有明显不同，即LV1与MV1、MV2的季节指数均呈强相关性，接近于完全相关，表明当谐波畸变合格时，低压侧线路与高压侧线路的季节波动几乎一致。

　　(4)本文算法不特定于变压器高低压线路，在实际工作中，可以从大量监测线路中筛选出与谐波源线路相关性较强的线路，从而给予重点关注，采取措施预防谐波源线路对它们产生影响；同时，也可用来分析各线路之间谐波变化的关系，为谐波管理和控制提供决策依据。

　　4结束语

　　(1)本文所设计的一种基于灰色模型的电力谐波相关性分析方法，引入灰色模型求取谐波数据的趋势值，可以挖掘谐波检测数据的非线性变化趋势，从而能准确的反映谐波源线路与非谐波源线路的谐波数据之间的趋势相关性。

　　(2)本方法设计了季节指数来体现谐波数据的季节波动性，通过求取季节指数的相关性，能反映出谐波源线路与非谐波源线路的电压总谐波畸变率的季节波动性之间的联系。

　　(3)本文所设计的方法可对电压谐波海量数据进行有效的挖掘，从大量馈线的检测数据中分析得到与谐波源线路相关性较强的线路（受谐波源污染／影响较严重的线路），为谐波的管理和治理提供有效的数据支持和决策依据，具有较高的使用价值，适用范围广。

　　参考文献：

　　[1]严静，邵振国．电能质量谐波监测与评估综述[J].电气技术，2020,21(7):1-7.

　　[2]江友华，陈博，田书锦．分布式谐波监测点优化与精度评估策略研究[J].上海电力学院学报，2019,35(1):43-52.

　　[3]国网宁夏电力有限公司电力科学研究院．配电网大数据挖掘分析方法及应用[M].北京：中国电力出版社，2021.

　　[4]张煊，刘宗杰．配电网中谐波源定位与检测方法研究[J].电工技术，2020(4):127-128.

　　[5]陈少伟，邵振国．基于最大后验估计的谐波源定位[J].电力系统及其自动化学报，2019,31(12):64-69.

　　[6]麦晓庆，张燕，张天湖，等．考虑系统运行方式变化的多谐波源责任划分[J].供用电，2023,40(5):34-43,60.

　　[7]丁同，陈红坤，吴斌，等．多谐波源定位及谐波责任量化区分方法综述[J].电力自动化设备，2020,40(1):19-30.

　　[8]张晨浩，李洋，宋国兵，等．基于模型识别的配电网谐波源定位方法[J].中国电机工程学报，2021,41(17):5803-5813.

　　[9]叶宗彬，侯波，张延澳，等．一种三相对称系统快速谐波检测算法[J].电工技术学报，2023,38(2):510-522.

　　[10]Herath H M S,McHardy S.Power quality trends in energy Australia distribution network[C]//IEEE 13th International Conference on Harmonics and Quality Power,September 28 2008-October 1,2008,Wollongong.Wollongong:University of Wollongong,2008.

　　[11]陶飞达，黄智鹏，王东芳，等．配电网故障智能诊断技术综述[J].机电工程技术，2020,49(1):16-18.

　　[12]桂海涛，田君杨，金益煊，等．基于数据关联分析的配电网谐波问题研究及薄弱点辨识方法[J].电工技术，2021(20):130-134.

　　[13]杨坦，蔡志杰．基于非侵入式负荷监测与分解的电力数据挖掘[J].数学建模及其应用，2018,7(4):30-36,48.

　　[14]徐昌宝，丁健，潘成达，等．基于大数据深化分析的电能质量扰动辨识方法研究[J].电网与清洁能源，2022,38(12):33-40.

　　[15]李寒，张成宇，王同勋，等．基于电力大数据的谐波仿真系统[J].计算机系统应用，2019,28(8):87-94.

　　[16]陈砚圃，杨一鸣，解云虹，等．一种基于准均匀采样的电力谐波分析方法[J].电力系统保护与控制，2022,50(16):115-120.

　　[17]刘光辉，朱婷婷，张慧娥．基于大数据技术的电能质量信息状态监测平台[J].自动化与仪表，2021,36(4):1-5,39.

　　[18]田铮．时间序列的理论与方法[M].北京：高等教育出版社，2004.

　　[19]邓聚龙．灰色预测与理论[M].武汉：华中理工大学出版社，1996.

　　[20]GB/T 24337—2009,电能质量－公用电网间谐波[S].