摘要：采用试验与仿真相结合的方法，对干式变压器在自然冷却条件下的温度场特性展开了系统的研究。首先，采用高低压绕组同时施加额定直流电流的试验方法，排除了涡流效应对高低压绕组损耗结果的影响，准确地获得了绕组损耗与温升的对应关系。同时，利用ＳＴＡＲ－ＣＣＭ ＋软件，分析了达到热平衡后，变压器内部温度场和流场的分布情况以及不同的湍流模型选取和绕组等效建模方法对温升模拟结果的影响规律。研究结果表明，由于空气自然对流的影响，高低压绕组的温度场分布规律基本相同，即：底端温度最低且温度随绕组高度的增加逐渐升高。此外，采用ｋ －ε低雷诺湍流模型和柱坐标等效建模法所得到的变压器自冷温升的仿真结果与试验结果的误差最小，且具有最快的收敛速度。所提出的仿真方法能够准确、快速地对自冷条件下干式变压器的温度场特性进行分析，可为变压器的设计与优化提供一定的指导与参考。

　　关键词：干式变压器；自然冷却；温度场仿真；数值模拟

　　０　 引言

　　作为电力系统中的关键电气设备，近年来干式变压器的发展愈发迅速，在我国电力变压器中所占的比例已超过４０％ 。因此，其安全、稳定的工作能力将直接影响整个电力系统的运行，有着举足轻重的作用［１ －２］。由于干式变压器通常采用环氧树脂作为绝缘材料，过高的温升不仅会加速老化影响寿命，还会造成绝缘击穿引发事故［３ －５］。因此，针对变压器的温度场分布展开准确、有效的预测，是使其能够长期安全运行的关键［６］。 目前，变压器温度场的研究方法主要有直接测量法和间接计算法两种。直接测量法主要通过红外测温仪、热电偶等传感器直接对测点温度进行采集［７］。间接计算法包括热路模型法［８］和数值模拟法［９］。特别是近年来随着计算机仿真技术的发展，越来越多的国内外学者开展了关于变压器温度场的数值仿真研究［１０ －１４］。值得注意的是，影响数值仿真结果的因素众多，而且当前不同文献中所采用的绕组简化方法、等效参数设置和湍流模型选择等均不尽相同［１５ －１８］。上述因素均会对数值仿真结果的准确性造成显著的影响，甚至导致错误的结果，这也在一定程度上给干式变压器的温度场仿真分析造成了困难［１９ －２０］。

　　为此，本文从温度场仿真的两个关键影响因素，即：湍流模型选取和绕组等效建模方法入手，针对自冷条件下干式变压器的温度场仿真方法展开了系统的研究。分析了流场和温度场的分布规律；并通过绕组温升试验和仿真结果的对比验证，评估了不同算法和方法之间的差异与优劣，为更加准确、有效的变压器温度场仿真计算提供了理论依据和数据支持。

　　１　 变压器温升试验及数值仿真

　　１. １　 温升试验方案

　　干式变压器在运行时所产生的各类损耗，如：磁滞损耗、涡流损耗、电阻损耗和杂散损耗等，是导致其温度上升的根本原因。值得注意的是，由于涡流效应的存在，交流试验条件下并不能精确地获得高低压绕组各的损耗结果。因此，为了更准确地研究绕组损耗与温升之间的关系，本文采用如图１ 所示的试验装置，对ＳＣＢ１０ －１０００ ／ １０ 变压器Ｃ 相的高低压绕组同时进行额定的直流加载。

　　通过上述方法，避免了绕组中的涡流损耗，从而能够准确地获得其电阻损耗，并作为模拟的直接输入参数。本次试验中，低压和高压绕组的损耗分别为：９７１. ５ Ｗ和１ ４３３. ９ Ｗ。基于高低压绕组的自冷温升测试数据和模拟结果的对比，进而明确变压器的仿真建模方法和相关的参数设置。

　　１. ２　 数值仿真建模

　　１. ２. １　 ＳＴＡＲ－ＣＣＭ ＋温度场仿真原理

　　变压器因损耗而产生的热量，将以热传导、热对流和热辐射的形式从内部传递到外部环境当中。变压器内部的热流路径由各部分的温差所决定，而温差的大小又与其内部损耗和流场的性质密切相关。因此，变压器的温度场模拟，本质上是利用传热学和流体力学的基本原理，并根据动量守恒和质能守恒方程来求解其流场和温度场分布的一个过程。

　　根据传热学理论，热量传递的控制方程主要有：

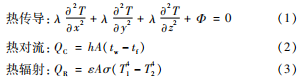
　　式中：λ为导热系数；ｈ为对流换热系数；Ａ为表面积；ε为发射率；σ为辐射常数。

　　此外，根据流体力学理论，变压器内部流场还需满足以下三大控制方程：

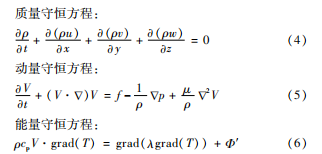
　　式中：ρ为密度；ｔ为时间；Ｖ为速度；ｐ为压强；μ为黏度； ｃｐ 为比热容；Φ′为热源项。

　　ＳＴＡＲ－ＣＣＭ ＋中的稳态求解器和分离变量算法将通过联立求解上述的偏微分方程组，获得变压器整体的速度场和温度场的分布情况。

　　１. ２. ２　 变压器三维模型的建立

　　ＳＣＢ１０－ １０００ ／ １０ 变压器绕组的三维数值模型如图２所示，低压绕组、高压绕组分别采用树脂固化和树脂浇注工艺制备。其中，低压绕组为箔绕结构，每层铜箔之间衬有绝缘布间隔；高压绕组为线绕结构，每匝铜线之间衬有绝缘纸间隔。其他小尺寸结构件的影响忽略不计。根据绕组结构的对称性，采用１ ／ ２ 模型简化计算，并在对称面施加对称边界。绕组周围的空气域应足够大，以保证模拟结果不受压力出口边界的影响。将实测损耗值转换为单位体积热源分别施加在低压（１０１ １９５. ２ Ｗ ／ ｍ３）和高压绕组（７４ ４４９. ６ Ｗ ／ ｍ３）之上。采用ＳＴＡＲ－ＣＣＭ ＋中的多面体网格对结构进行离散，总体网格数量为１ ４６３ ０２６。

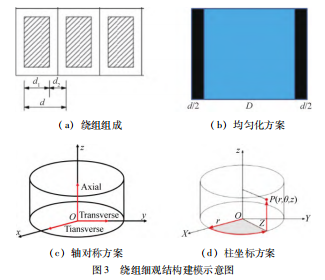
　　对于自然冷却下的变压器温度场仿真而言，空气的湍流模型和绕组的细观建模是温升结果最主要的影响因素。本文中，开启Ｂｏｕｓｓｉｎｅｓｑ近似模型来求解非等温流动中空气的自然对流问题；对于空气湍流模型，本文选取了文献当中经常采用的Ｒｅａｌｉｚａｂｌｅ ｋ － ε 、ｋ － ε低雷诺和ｋ － ω ＳＳＴ三种模型。此外，对于重点关注的高低压绕组而言，其主要由导体和匝间绝缘组成，是一个典型的复合材料，如图３ （ａ）所示，因此导热系数会表现出明显的各向异性；且由于计算资源有限，三维仿真时无法将导体和匝间绝缘一一建出，必须采用等效的方法将其建为一个整体，并赋予相应的材料参数。以往出于简化计算的目的，通常直接赋予绕组铜或铝的导热系数，这显然会不可避免地带来误差。因此，本文提出了以下３ 种方案来考虑匝间绝缘对绕组导热系数的影响。

　　（１）均匀化方案：将内部的匝间绝缘均匀等效至绕组两侧，并分别赋予导体和绝缘各向同性的真实导热系数λ，如图３ （ｂ）所示。

　　（２）轴对称方案：采用轴对称坐标表征绕组的各向异性行为，在Ｚ轴上和ＸＹ面内分别赋予真实导热系数λ和等效导热系数λＤ ，如图３ （ｃ）所示。

　　（３）柱坐标方案：采用柱坐标描述环形绕组的各向异性行为，其轴向、环向和径向的导热系数分别为λ 、λ和λＤ ，如图３ （ｄ）所示。

　　２　 结果与讨论

　　２. １　 变压器的温度／速度场分布

　　设置环境温度为２７ ℃ ，开始变压器温升计算。图４给出了变压器整体在达到热平衡后的稳态温度场和速度场分布云图。

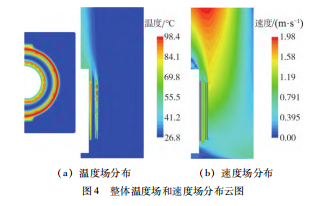
　　图４ （ａ）表明，低压和高压绕组的温度变化规律基本相同，均为底端温度最低，并随着绕组高度的增加逐渐升高，而在接近绕组顶端处又略微降低。导致此现象的原因可从图４ （ｂ）的速度场分布云图中得出：自然冷却条件下，绕组通过传导、对流和辐射的方式将周围空气加热，随着温度的升高，空气开始发生自然对流，热空气逐渐上浮并向顶端流动。并且，由于气体黏性和壁面粗糙度的影响，在靠近绕组壁面处的空气流速会迅速降低，形成一层极薄的速度边界层和温度边界层。随着绕组高度的增加，速度边界层和温度边界层逐渐变厚、局部换热系数和温度梯度均逐渐降低，从而导致对流换热和热传导效果的下降。值得一提的是，流体力学中通常利用普朗特数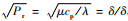来表征传热过程中速度边界层δ与温度边界层δＴ 之比。对于空气而言，该值约等于１。而图４ 中模拟得到的速度和温度边界层具有大致相等的厚度，这进一步说明了数值仿真的准确性。此外，因为绕组顶端具有较为开阔的散热空间，所以在接近顶端处，绕组的温度会有一定程度的减小。

　　２. ２　 湍流模型对温升的影响

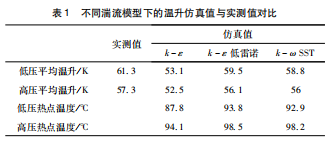
　　表１给出了不同湍流模型下温升的仿真结果与试验结果的对比。从中可以看出，ｋ － ε低雷诺湍流模型的温升结果误差最小（约为３％ ），其次为ｋ － ω ＳＳＴ湍流模型，Ｒｅａｌｉｚａｂｌｅ ｋ － ε湍流模型的误差则最大。此现象可以利用流体力学中的两个无量纲参数，即：格拉晓夫数和雷诺数来进行解释。

　　格拉晓夫数表征了流体浮升力与滞力的比值：

　　式中：ｇ为重力加速度；αｐ 为热膨胀系数。

　　当浮升力大于黏滞力时流态为湍流，否则为层流。变压器的特征长度Ｌ一般为１ ｍ、温升ΔＴ通常在５０ ～１００ Ｋ， 此时Ｇｒ 的量级为１０９，处于层流与湍流转化的临界点。

　　雷诺数表征了流体惯性力与粘性力的比值：

　　对于变压器自冷试验，其表面空气流速Ｖ 一般在１. ５ ｍ ／ ｓ左右、特征长度Ｌ′一般为０. １ ｍ左右，此时雷诺数通常介于２ ０００ ～１０ ０００之间，同样处于层流向湍流转变的过渡状态。

　　由上述分析可知，自然冷却条件下，变压器绕组附近的空气一般处于过渡流态，其雷诺数较低。因此描述低雷诺条件下的ｋ － ω ＳＳＴ和ｋ － ε低雷诺湍流模型能够较好的模拟自冷温升行为；而Ｒｅａｌｉｚａｂｌｅ ｋ － ε模型一般适用于高雷诺数流动，因此误差相对较大。

　　２. ３　 绕组建模对温升的影响

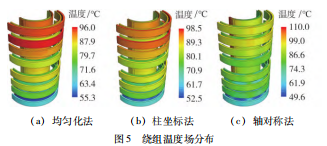
　　表２所示为不同绕组建模方案对温升仿真结果的影响规律。可以看出，３ 种建模方案所得出的绕组平均温升模拟值均与试验值较为相近，其中又以柱坐标建模方案的误差最小（约为２％ ）从图５的绕组温度分布场中可以看出，尽管轴对称建模方案在平均温升上与其余两者基本相同，但其温度场分布却较大的差异。特别是在低压铜排出线处的非圆形区域附近，会出现明显的局部高温，如图５ （ｃ）所示，从而给热点温升和位置的分析带来困难。

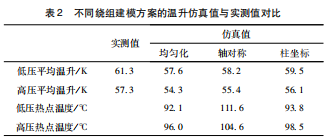
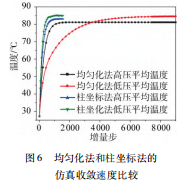
　　同时，均匀化建模方案和柱坐标建模方案的温度分布基本一致，均能够有效地反映绕组运行过程中的热点位置和温升情况。值得强调的是，相比于均匀化建模方案，柱坐标建模方案不仅具有更加明确的物理意义，同时在计算时还具有更快的收敛速度，其收敛步数约为均匀化建模方案的１ ／ ４，如图６所示。

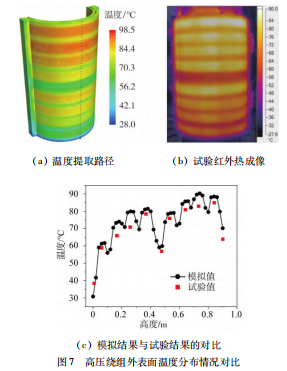
　　此外，本文提取了高压绕组外表面上沿高度方向的温度分布情况，如图７ （ａ）所示，并将其与试验获得的红外热成像图中的温度数据进行了对比，如图７ （ｂ）所示。从图７ （ｃ）中可以看出，模拟结果与试验结果相比具有较好的一致性，能够较为准确地描述高压绕组的温度分布及变化情况，从而进一步表明了本文所采用的建模方案的有效性。

　　３　 结束语

　　本文通过试验和模拟相结合的方法，对干式变压器在自然冷却条件下的温度场仿真方法及其分布规律进行了研究，并得到以下结论。

　　（１）根据理论分析可知，自冷条件下变压器附近的空气基本处于过渡流态，具有较低的雷诺数。因此，选择ｋ － ε低雷诺湍流模型能够获得比Ｒｅａｌｉｚａｂｌｅ ｋ － ε湍流模型更为准确和合理的温升模拟结果。

　　（２）对于高低压绕组的温度场仿真，采用柱坐标法并赋予其等效导热系数的建模方案相比于其他方法，物理意义更加明确、模拟结果更加准确、计算效率更加高效。

　　上述结论将为干式变压器的温度场仿真与分析提供一定的参考价值。

　　参考文献：

　　［１］孙林，王梦云，翟向向，等．我国电力变压器发展现状及趋势［Ｊ］．电力设备，２００３（４）：７８－８１．

　　［２］黄娇．干式变压器温度场的研究［Ｄ］． 青岛：山东科技大学，２０１７．

　　［３］尹克宁．变压器设计原理［Ｍ］．北京：中国电力出版社，２００３．

　　［４］胡新舟，肖珞琼．船舶推进干式变压器热量分析［Ｊ］．机电工程技术，２０２２，５１（１）：１９１ － １９４．

　　［５］张能． 变压器内部热量传导规律及分布式测温系统研究［Ｄ］．武汉：华中科技大学，２０１７．

　　［６］王永强，张晓霞，欧阳宝龙，等．基于反传热模型的干式变压器绕组热点温度计算［Ｊ］．电测与仪表，２０１６ （１０）：１１５－１２１．

　　［７］李涛，张艳． 变压器温升试验研究［Ｊ］． 甘肃科技，２０２２，３８（１６）：４５－４８．

　　［８］唐钊，刘轩东，陈铭．考虑流体动力学的干式变压器热网络模型仿真分析［Ｊ］．电工技术学报，２０２２，３７（１８）：４７７７－４７８７．

　　［９］Ｅｓｌａｍｉａｎ Ｍ，Ｖａｈｉｄｉ Ｂ，Ｅｓｌａｍｉａｎ Ａ． Ｔｈｅｒｍａｌ ａｎａｌｙｓｉｓ ｏｆ ｃａｓｔ －ｒｅｓｉｎ ｄｒｙ－ｔｙｐｅ ｔｒａｎｓｆｏｒｍｅｒｓ［Ｊ］． Ｅｎｅｒｇｙ Ｃｏｎｖｅｒｓｉｏｎ ａｎｄ Ｍａｎａｇｅｍｅｎｔ， ２０１１，５２（７）：２４７９－２４８８．

　　［１０］Ｌｉｕ Ｃ，Ｒｕａｎ Ｊ，Ｗｅｎ Ｗ，ｅｔ ａｌ． Ｔｅｍｐｅｒａｔｕｒｅ ｒｉｓｅ ｏｆ ａ ｄｒｙ － ｔｙｐｅ ｔｒａｎｓｆｏｒｍｅｒ ｗｉｔｈ ｑｕａｓｉ － ３Ｄ ｃｏｕｐｌｅｄ － ｆｉｅｌｄ ｍｅｔｈｏｄ ［Ｊ］． ＩＥＴＥｌｅｃｔｒｉｃ Ｐｏｗｅｒ Ａｐｐｌｉｃａｔｉｏｎｓ，２０１６，１０（７）：５９８－６０３．

　　［１１］侯国柱，曹效义，张晓妍．大容量主变压器在２２０ ｋＶ电网变电站中的应用分析［Ｊ］．内蒙古电力技术，２０２２，４０（２）：８４－８８．

　　［１２］田慕琴，朱晶晶，宋建成，等．基于流固耦合分析的矿用干式变压器温度场仿真［Ｊ］．高电压技术，２０１６，４２（１２）：３９７２－３９８１．

　　［１３］熊兰，赵艳龙，杨子康，等．树脂浇注干式变压器温升分析与计算［Ｊ］．高电压技术，２０１３，３９（２）：２６５－２７１．

　　［１４］刘国坚，王丰华．树脂浇注干式变压器温度场分布的计算分析［Ｊ］．高压电器，２０１６，５２（８）：８３－８９．

　　［１５］许亚迪，李琳． 高频变压器电磁－温度场耦合计算与实验［Ｊ］．电力电子技术，２０２２，５６（１２）：１２６－１３５．

　　［１６］兰贞波，文武，阮江军，等．基于有限元法的干式变压器多物理场分析计算［Ｊ］．高压电器，２０１５，５１（８）：１０７－１１３．

　　［１７］邓永清，阮江军，龚宇佳，等．基于参数热等效的１０ｋＶ 变压器温度流体场三维仿真计算［Ｊ］．电力自动化设备，２０２１，４１（４）：２１２－２１８．

　　［１８］吴红菊，贺银涛．基于温度场仿真分析的干式变压器散热设计［Ｊ］．机电工程技术，２０１９，４８（８）：１８３ － １８５．

　　［１９］黄超洋，杨宗．风冷变压器室热仿真计算及优化［Ｊ］．中国科技信息，２０１８，５７７（５）：７７－７８．

　　［２０］张牧，高立业，魏娟，等．树脂浇注干式变压器三维温度场仿真计算［Ｊ］．天津工业大学学报，２０１５，３４（３）：６２－６６．