摘要：对于斜面上的孔，尤其是对细孔、斜孔进行形状参数及位置参数的测量，单独使用普通三坐标测量仪或精密影像式测绘仪，由于测量设备的自身特点，均具有较大的局限性。在结合三坐标测量仪能够对斜平面的空间坐标精密测量与影像测量仪能够对水平面上的轮廓坐标精密测绘的基础上，利用通孔的同轴性、孔的轴向方向向量与不同加工面的夹角具有对应关系，斜平面水平放置时测量的相对点坐标，等价于测量的轮廓相对坐标是在斜平面上建立坐标系测量的值，以及斜面上建立的坐标系可以与世界坐标系通过线性变换进行对应等关系。通过对测量点坐标进行位置变换，计算并校正孔在不同平面和不同坐标系下测量的椭圆长、短半轴的长度，确定孔中心轴线与不同平面的夹角大小，从而计算出斜面椭圆的旋转角度，进而确定孔的直径、轴向向量等参数。

　　关键词：线性变换；轴向向量；校正

　　Measurement of Parameters such as Through Hole Radius and Axial Vector in Inclined Planes Using a Combination of Coordinate Measuring Instruments and Image Measuring Instruments

　　He Wenqing，Ruan Yi，Li Yingshu，Hu Guoying，Yu Ning

　　(Guangdong Machinery Research Institute Co.,Ltd.,Guangzhou 510799,China)

　　Abstract:For the measurement of shape and position parameters of holes on inclined planes,especially for fine and inclined holes,using a common coordinate measuring instrument or a precision imaging surveying instrument alone has significant limitations due to the characteristics of the measuring equipment.Three coordinate measuring instruments can accurately measure the spatial coordinates of oblique planes,while image measuring instruments can accurately measure the contour coordinates on horizontal planes.Based on this,using some corresponding relationships such as the corresponding relationship between the coaxiality of the through-hole,the axial direction vector of the hole,and the angle between different machining surfaces;the relative point coordinates measured when the inclined plane is horizontally placed are equivalent to the measured contour relative coordinates,which are the values measured by establishing a coordinate system on the inclined plane;the coordinate system established on the inclined plane can correspond to the world coordinate system through linear transformation.By transforming the position of the coordinates of the measuring point,calculating and correcting the length of the ellipse length and semi-axis measured in different planes and coordinate systems,the angle between the central axis of the hole and different planes is determined,so as to calculate the rotation angle of the beveled ellipse,and then determine the diameter,axial vector and other parameters of the hole.

　　Key words:linear transformation;axial vector;correction

　　0引言

　　影像测量技术是基于计算机应用的发展，通过图像采集器把提取的图像信息经软件进行分析，从而得到测量数据[1]。在测量阶段，由光学显微镜对待测物体进行高倍率光学放大成像，经过CCD摄像系统将放大后的物体影像送入计算机，能高效地检测各种复杂工件的轮廓和表面形状尺寸、角度及位置，特别是精密零部件的检测[2]。

　　三坐标测量仪(Coordinate Measurement Machine，CMM)是一种能够在六面体的空间范围内进行测量，并且能够表现被测对象几何形状、长度及圆周分度等特性的仪器，被广泛应用于汽车、电子、机械、航空、模具等行业中，具有高灵敏度及精确性[3]。在对结构复杂工件进行精密测量的过程中起着越来越重要的作用[4]。

　　回转体类工件是机械加工中非常重要的一部分，同时随着加工的精密度及设计复杂性的提高，产品孔位及方向变的日趋多样化[5]。在实际生产中，三坐标测量仪是孔类工件测量相关参数使用较为普遍的测量仪器。目前，三坐标测量仪通常采用接触式测量法，测量时零件的摆放位置、夹具选取工作尤为重要，当未能使用匹配的夹具完成装夹，对于测量数值以及最后的计算结果会产生不可忽视的影响[6]。

　　对于结构精细、待测尺寸较小的工件，影像测量仪可以通过放大倍率，方便精准测量，主要以二维测量为主[7]。在测量时，镜头与工件待测平面要呈垂直状态。当镜头光轴与被测表面不垂直时，工作表面投影面与工件平面存在一定的夹角，工件表面实际距离与投影面对应的距离不一致[8]。因此对于斜面上的孔，不能通过影像测量仪直接测量。

　　本文主要的目的是联合三坐标测量仪与影像测量仪对斜平面通孔半径、轴向向量等参数进行测量。通过查找文献，影像测量仪对轮廓的测量，需要轮廓处于同一水平面[9]。目前，对于斜孔及其在空间位置的测量主要是采用三坐标测量仪来完成，普通三坐标测量仪测量斜面上的未知角度的通孔时，对摆放位置、夹具、调试均有较高的要求，同时对于细孔的测量，由于测针上的杆与红宝石具有一定尺寸，对孔的尺寸大小、角度有一定的限制。

　　本文充分利用三坐标测量仪在测量斜面上点坐标的精确性，及影像测量仪能够采用高倍率光学成像的方式对平面轮廓进行高分辨率测量的优点。通过测量斜平面在测量时的点坐标、孔在两平面轮廓的相对坐标，再通过编写的脚本程序进行计算，可以得到比较精确的测量结果。涉及三坐标测量的部分对摆放位置及夹具没有特殊的要求；影像测量的部分对孔径大小也没有要求，涉及孔轮廓相对坐标的测量仅需要在夹具的辅助下水平放置进行影像测量，对于夹具的要求易于实现，具有较强的可操作性。

　　1测量原理和方法

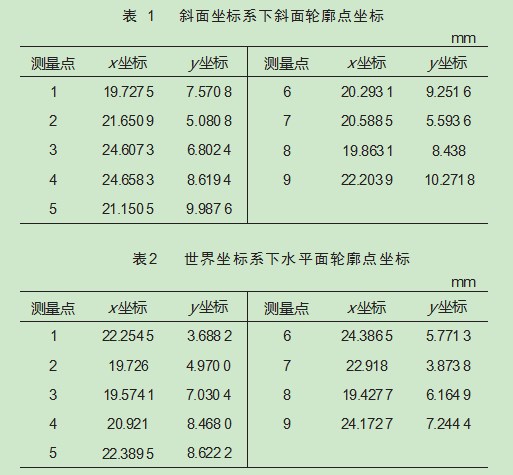
　　如图1所示，测量对象为有倾斜面的铝块，下表面为约25 mm×25mm的平面，斜面上有若干与水平面呈一定角度的直孔，孔径为同一规格小5 mm，为了验证方便，测绘、计算的孔为垂直于底面的孔。本文主要是为了测量斜面的斜面方程、孔的半径及孔中心轴线相对于斜面的方向向量。

　　1.1测量原理

　　使用旋转圆形刀具对待加工材料进行切削打孔的加工时，刀具的运动轨迹相当于圆柱体的不断延伸，与被加工材料进行差集。刀具与平面垂直时，孔在平面上的切削轮廓为圆形，不垂直时为椭圆形。

　　联合三坐标测量仪与精密影像式测绘仪，通过使用三坐标测量斜面在世界坐标系中的法向量(放置在%-y平面没有方向要求)，将底面反转并水平放置使用影像测绘仪测量孔轮廓点在世界坐标系中的相对坐标，及将斜面水平放置使用影像测绘仪测量孔轮廓点在世界坐标系中的相对坐标。运用孔的中心轴线的方向向量具有一致性、不同坐标系之间可以通过转换矩阵来实现线性变换等原理来实现孔中心轴向方向向量的计算[10]。主要可以归纳为以下方面。

　　(1)平面与圆柱刀具交集的形成的圆形或椭圆，圆形的直径与刀具一致，椭圆的短轴在理想状态下与孔直径一致。

　　(2)将斜面水平放置，测量出来的相对坐标，相当于是在斜面上建立坐标系，在斜面坐标系中测量出的相对坐标。已知斜面在世界坐标系的法向量，在世界坐标系的原点处建立与斜面平行的斜面及斜面坐标系，孔的轮廓在建立的斜面上与实际斜面上一致。同时平/斜面的相交，可以得到交线的方向向量。

　　(3)使用精密影像式测绘仪对平(斜)面上孔水平放置对轮廓进行测量，对轮廓进行拟合得到在相应平面上轮廓的长轴、短轴或直径的尺寸，从而得到孔的轴向与平面的夹角。

　　(4)建立的斜面坐标系与世界坐标系的原点重合，斜面坐标系与世界坐标系共用交线的方向向量作为一个坐标轴的轴方向，并通过已知的法向量建立两个坐标系的转换矩阵，从而实现坐标在两个坐标系之间的线性变换，如图2~3所示。

　　(5)在实际的工程实践中，上下两个孔轮廓具有相同的加工特性，直径与拟合尺寸与测量点的平均偏差相对一致，因此引入匹配度概念，对拟合的尺寸参数进行校正。

　　(6)由于孔具有同轴性，在斜面坐标系中孔的轴向向量经过线性变换后，与在世界坐标系中拟合底平面孔轮廓得到的轴向向量重合。本文是通过z分量的重合，计算斜面上椭圆长轴的转动角度，具有唯一性。

　　测量流程如图4所示，通过三坐标测量仪测量工件斜平面的法向量，使用影像式测绘仪测量在斜面、底平面孔轮廓在不同坐标系下的相对坐标，再采用最小二乘法进行斜平面、两个椭圆轮廓的拟合。对椭圆及轮廓点坐标进行平移及旋转，使椭圆中心与原点重合及长轴与各自坐标系的x轴重合。确定孔的中心轴线与斜平面、底平面的夹角大小及两个坐标系之间的转换矩阵。然后通过通孔两轮廓的匹配度对拟合椭圆的长、短半径进行校正，再计算斜平面通孔半径、轴向向量等参数。

　　1.2数学分析方法

　　1.2.1平面最小二乘法椭圆方程拟合及参数计算

　　设平面任意位置椭圆方程为：

　　解方程可以得到A、B、C、D、E的值。

　　根据椭圆的几何知识，可以计算出椭圆的5个参数：位置参数(θ,x0,y0)以及形状参数(a,b,θ)。

　　1.2.2确认孔的中心轴线与平面的夹角α

　　根据孔在水平面的椭圆长度轴，确认孔的中心轴线与平面的夹角α。

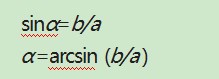
　　式中：a为椭圆的长轴长度；b为椭圆的短轴长度。

　　1.2.3直线的方向向量

　　在斜面坐标系中，直线与x-y平面的夹角为α，直线水平面上的投影与x轴的夹角为θ，轴向方向上的线段模为R时，在x轴上的投影长度为Rcos(α)cos(θ)；在y轴上的投影长度为Rcos(α)sin(θ)；在z轴上的投影长度为R sin(θ)。直线的方向向量可以表示为：[cos(α)cos(θ)cos(α)sin(θ)sin(α)]。

　　1.2.4最小二乘法拟合平面方程

　　可将上式用矩阵的形式进行表达

　　2测量步骤

　　2.1三坐标测量仪的测量

　　在世界坐标系下测量斜面的坐标点(5个)、孔的轴向方向向量与直径。

　　2.2精密影像式测绘仪的测量

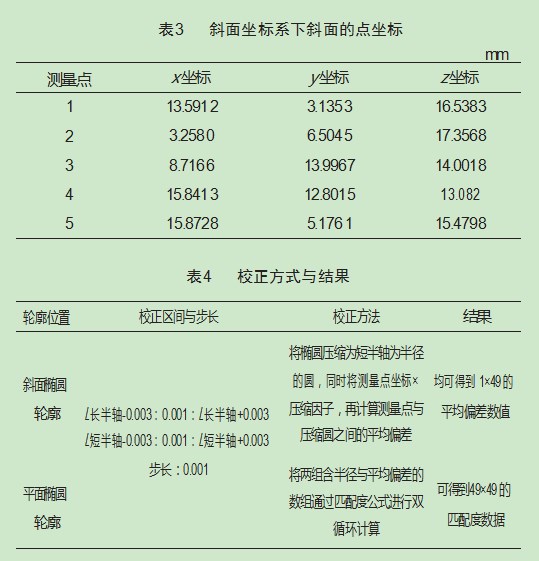
　　测量斜面上孔的轮廓在将斜面水平放置下的相对坐标(图5)；测量平面上孔的轮廓在将底面反转水平放置时的相对坐标(图6)。

　　2.3使用python 4.2.1编写数据处理脚本进行数据分析

　　(1)建立平面拟合方程1：

　　plane_fit(Pi(xi，yi)(i=1，2，3，…，N)，A，B，C，D)

　　//(Pi(xi，yi)(i=1，2，3，…，N)，为三坐标测量的斜面点坐标，N=5

　　//输入：(Pi(xi，yi)(i=1，2，3，…，N)N=5，为三坐标测量的斜面点坐标

　　//输出：A，B，C，D，即斜面在世界坐标系下的平面拟合方程1：Ax+By+Cz+D=0

　　(2)将平面拟合方程平行移动至过原点，并令C=0，即为平面拟合方程2：a0 x+a 1 y-z=0，平面拟合方程2与水平面交线为：

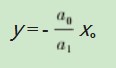
　　(3)在拟合平面2上建立三维直角坐标系斜面坐标系与世界坐标系之间的线性转换关系。向量u 1=[a0 a 1-1]为新建坐标系的z轴方向向量，利用原点及平面上一点u2=[1 0 a0](交线上的一点)建立坐标系的x轴方向向量，y轴方向向量u3=u 1×u2。并将3个轴向量单位化：U1=[ax ay az]；U2=[bx by bz]；U3=[cx cy cz]。

　　(4)斜面坐标系与世界坐标系之间的线性转换关系，斜面坐标系中的轴线向量设为k=[k 1 k2 k3]，其中k为单位向量。则有：

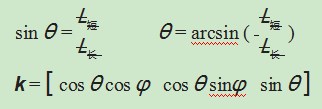
　　式中：θ为轴线与斜平面的夹角；L短、L长分别为拟合椭圆的短、长轴的长度；φ为轴线与x轴线的夹角。

　　因为机器坐标系与斜面的坐标系是同一个原点，因此向量的转换也即是点的转换。斜面坐标系中的点[k 1 k2 k3]，转换至机器坐标系中，可得点的转换坐标[k 11 k21 k31]：

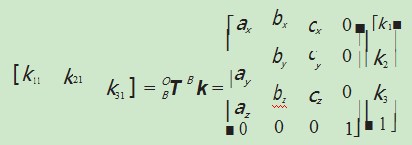
　　式中：T为斜面坐标系转换至机器坐标系的转换矩阵。

　　转换后的向量为[k 11 k21 k31]，与水平面的夹角设为η，sinη=k31，即η=arcsin k31。由于孔具有同轴性，因此arcsin k31=arcsin(l短/l长)，可以解出唯一值φ。其中l短、l长分别为机器坐标系中水平面拟合椭圆的长、短轴的长度。

　　(5)对世界坐标系的底平面孔轮廓的相对坐标进行椭圆拟合，对斜面上孔轮廓的相对坐标在斜面坐标系下进行椭圆拟合，确定各自在坐标系中的中心点、长短轴、倾角角度等参数。

　　ellipse_fit(A_test[0..p]，x0，y0，semimajor，semiminor，phi)

　　ellipse_fit(B_test[0..p]，x0，y0，semimajor，semiminor，phi)

　　//输入：A_test[0..p]；B_test(0..q)

　　//输出：各自的[a，b，c，d，f，g，semimajor，semimi⁃nor，x0，y0，phi]

　　//A_test[0..p]；B_test(0..q)分别为椭圆轮廓的测量坐标

　　(6)分别对轮廓坐标进行平移及旋转，使中心点与原点重合，同时对坐标点集进行旋转(phi)角度，使拟合的椭圆的长轴与各自坐标系的x轴重合。

　　//x_new=xi-x0；y_new=yi-y0

　　//[x_new，y_new]=[xi，yi]*[cos(phi)，-sin(phi)；sin(phi)，cos(phi)]

　　(7)校正孔的轴向方向向量。测量始终会有误差的存在，本文采用孔的同轴性原理，利用轴心与两平面的夹角具有对应关系的方法进行相对轴心向量的测量，因此对于两椭圆轮廓的长、短轴的精度要求较高，需要对测量点坐标最小二乘法拟合的基础上进行校正。在工程实际的精密加工中，孔的两端轮廓的尺寸参数具有较强的一致性，如直径、偏差等。

　　本文中的椭圆轮廓是采用旋转刀具进行切削加工形成，可以认为是通过与椭圆短轴一致的圆拉伸形成。通过对两椭圆的长、短轴进行±Δ(±0.003 mm)区间进行校正，将拟合椭圆通过与压缩因子(μ=短半轴长/长半轴长)相乘，椭圆压缩为与椭圆短轴一致的圆，同时测量的点x坐标与压缩因子相乘，并计算转换后的点坐标与变换后的圆的平均误差λ，使用匹配度ξ作为校正尺寸的确定标准。

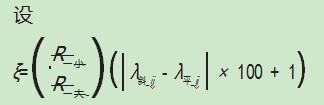
　　式中：ξ为匹配度，匹配度越接近1，匹配情况越好；R_大为两椭圆压缩后，较大圆的半径值；R_小为两椭圆压缩后，较小圆的半径值；i为R的个数系数(1~7)；j为平均偏差的个数系数(1~7)。

　　确定好两个椭圆轮廓的长、短轴尺寸后，计算斜面椭圆的旋转角度，然后计算出孔的轴向方向向量。

　　3实验结果与分析

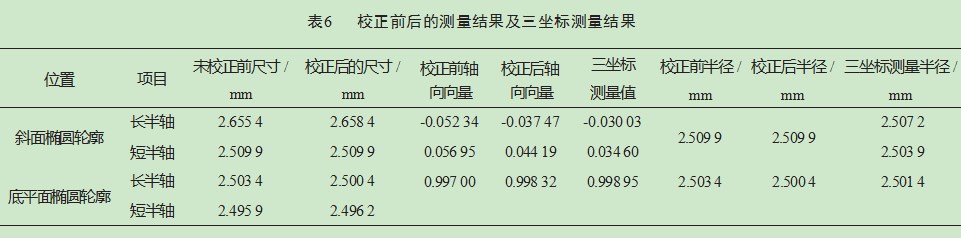
　　对实验测量的数据进行程序计算与分析，具体数据、测量及计算结果如表1~6所示。

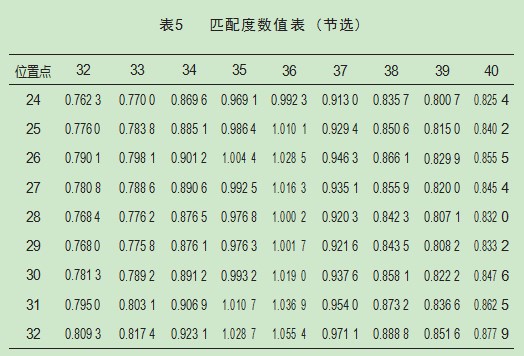
　　根据匹配度公式可知，孔两端的截面圆的半径差、测量的平均偏差的乘积越接近1，截面的相似度高，匹配程度越好。表5为节选的匹配度数据。

　　经过搜索匹配表中与1最为接近的匹配度，第[28，36]的匹配度符合要求，该匹配度对应的斜面椭圆轮廓的参数为(校正前短半轴+0，校正前长半轴+0.003)；平面椭圆轮廓的参数为(校正前短半轴+0.001，校正前长半轴-0.003)。

　　从表6可以看出，利用三坐标与影像测量仪联合测量，以三坐标测量结果为标准，校正前后的测量值均具有较高的精度，说明通过本文的测量、处理数据的方法，能充分利用仪器的高精度、孔在不同加工平面有相互关联等特点，完成孔的相关参数较高精度的测量。校正前后的轴向向量与三坐标仪器的测量结果相比，校正后的轴向向量与三坐标的测量结果更为接近，表明通过校正能对测量误差带来的拟合误差进行修正，进一步提高测量的精度。

　　4结束语

　　本文测量的斜平面通孔半径、孔轴向向量等参数，是基于三坐标测量时的斜平面的法向量，通过测量孔在不同平面轮廓的相对坐标，根据孔的轴心在不同平面具有同轴性及夹角的对应关系，对测量的相对点坐标进行拟合、转换、校正，并通过编写的脚本程序完成计算。在本次测量中，采用影像测量仪对不同平面的轮廓进行测量时，保证测量平面的水平程度，是本次测量的关键。

　　在实际的工作运用中，如对斜面的孔进行重绘，当斜面法向量改变时，孔的轴向向量需要根据斜面法向量变化前后的关系进行转换。同时本文的测量，没有涉及对孔在平面/空间上的位置定位，需要对工件外形进行测量后，确定平/斜上孔的轮廓的拟合中心与边缘的约束尺寸，才能完成孔在工件上的定位。

　　[1]刘俊汉.彭艺.影像测量仪光学成像系统对测量的影响及测量结果不确定度分[J].电子测试,2022,36(18):38-40.

　　[2]周雷.CCD非接触几何量测量系统的设计与实现[D].大连:大连理工大学,2008.

　　[3]王亮,于颖.面向工业4.0的三坐标测量仪教学功能开发[J].实验室研究与探索,2020,39(5):208-211.

　　[4]朱敏涛,路世锋,宋兵.三坐标测量方法与实际应用探讨[J].科技风,2016(18):242-243.

　　[5]王跃军.三坐标测量斜孔圆柱度的方法研究[J].计测技术,2017,37(S1):16-22.

　　[6]宣默涵,于昕平.三坐标测量斜孔零件的应用研究[J].新技术新工艺,2022(9):70-74.

　　[7]韩梅.影像测量仪在检测中的应用[J].汽车实用技术,2016(8):176-179.

　　[8]敖荟兰.影像测量仪误差分析及控制[J].印制电路信息,2018,26(4):25-30.

　　[9]陆屹立.基于二维投影式光学传感器的轴类零件测量研究[D].杭州:中国计量大学,2022.

　　[10]李聪利,徐善军.基于双目视觉的电力机器人三维定位方法[J].制造业自动化,2021,43(10):138-143.