摘要：为了准确检测高压断路器弹簧操动机构状态以及时发现故障,人工设置了合闸弹簧疲劳与合闸电磁铁铁心松动故障。测量两种故障状态与正常状态下的断路器合闸振动信号，对振动信号进行5层小波包分解后计算能量谱作为故障诊断特征向量。使用主成分分析对能量谱进行降维，计算结果表明主成分1与主成分2贡献了原始特征向量98%的信息。以能量谱主成分1与主成分2作为最终模型的特征参数，基于支持向量机建立了断路器操动机构故障诊断模型，结果表明模型能够正确识别测试集所有样本的故障类型。作为对比，使用未降维前的小波包能量谱建立的模型识别准确率为86.6%，主成分分析降维后有效提高了模型的准确率，为100%。

　　关键词：机械故障；小波包；主成分分析；支持向量机

　　Abstract:In order to accurately detect the state of the operating mechanism of the high voltage circuit breaker spring and find the fault in time,the fatigue of the closing spring and the loosening of the closing electromagnet core are set manually.Two kinds of fault state and the normal state of the circuit breaker closing vibration signal are measured,the vibration signal is decomposed by 5-layer wavelet packet,and the energy spectrum is calculated as the fault diagnosis feature vector.The results show that principal component 1 and principal component 2 contribute 98%of the information of the original eigenvector.Based on support vector machine,a fault diagnosis model of circuit breaker operating mechanism is established with energy spectrum principal component 1 and principal component 2 as the characteristic parameters of the final model.In contrast,the model recognition accuracy using the wavelet packet energy spectrum before dimensionality reduction is only 86.6%,and the accuracy of the model is effectively improved after dimensionality reduction by principal component analysis.

　　Key words:mechanical fault;wavelet packet;principal component analysis;support vector machine

　　0引言

　　高压断路器为电力系统中的重要开关设备，担任着控制和保护的双重作用，需要迅速高效地完成线路的投切与短路电流的切断等任务，而断路器动作的速度与可靠性由操动机构决定。由于动作过程中操动机构承受着巨大的机械载荷，随着动作次数的增加，操动机构不可避免地会出现机械性能的劣化[1-3]，导致断路器动作的可靠性降低，当出现较严重的故障时甚至可能会导致拒动，严重威胁电网的安全可靠运行。因此及时发现操动机构机械故障并进行相应的运维检修措施，对于提高电力系统的安全性与可靠性具有重要的意义[4-7]。

　　断路器分合闸过程中的振动信号蕴含丰富的操动机构状态信息，衰减小，通过测量振动信号能够实现对操动机构的非侵入式检测。许多学者研究了基于振动信号的断路器操动机构机械故障识别。文献[8]通过对振动号进行局部均值分解后提取能量特征，改善了经验模态分解易产生端点效应，过包络与欠包络的不足。文献[9]使用振动信号的分形特征进行轴承机械故障的诊断，计算了不同类型故障的广义分形维数，通过分形维数谱的差异实现了3种故障状态与正常状态的分类识别。文献[10]对比短时傅里叶变换、小波包变换与希尔伯特-黄变换3种特征提取方法，结果显示小波包变换得到的特征向量具有最佳的故障分类性能。

　　本文测量合闸过程中的振动信号，利用小波包分解后的各频带分量能量谱作为特征向量，结合主成分分析进行特征量的降维，最后基于支持向量机进行了断路器操动机构故障的分类识别。

　　1振动信号特征提取方法

　　1.1小波包—能量谱

　　针对小波变换“高频低分辨率”的缺点，通过对信号的低频部分与高频部分同时进行分解，发展出了小波包变换(Wavelet Package Transform，WPT)。相比小波变换，小波包变换具有更高的高频分辨率，从而更加适合于对高频成分较多的信号进行分析[11-12]。断路器振动信号具有频率高、局部信息丰富的特点，因此选择小波包变换对振动信号进行分析。小波包变换原理如下。

　　对于原始信号d=f(n)，其小波包分解可表示为式中：

      d,2n+1分别为高通滤波器与低通滤波器下的小波包分解第l层的节点(j，n)的节点系数；hk-2l、gk-2l为高通与低通滤波器；d+1,n为小波包第k层节点(j+1，n)的节点系数。

　　由于每次分解都将频段分解为高频与低频两个部分，因此小波包分解是“二叉树”式的分解，当对原始信号进行n层分解时则得到2n个频段，每个频段的范围相同[13-15]。随着分解层数的增加，频带内的信号分辨率也随之增加，3层小波包分解的示意图如图1所示，其中S代表低频分量，D代表高频分量。

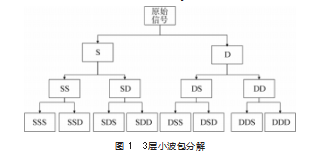
　　小波包-能量谱是以能量方式表示小波包分解的结果。选取分解后各个频带的信号Sj(t)的平方随时间的积分作为能量的标志，第j个频带的能量Ej的表达式为：

　　小波包分解的过程中信号能量保持守恒，分解后各个频带的能量之和与原始信号的能量S相等。因此可以选择分解后各个频带的能量占总能量的百分比作为特征向量，即能量谱，如式(3)所示。

　　Q=[E 1/E,E2/E,…,Ej/E]（3）
       其中，E为总能量。

　　1.2主成分分析

　　降低特征向量维度对于提高分类模型的准确率和效率具有重要的意义。主成分分析法(Principal Component Analysis，PCA)就是一种去除相关性与冗余性的数据线性降维算法[16-18]。其基本思想是将原始属性向量线性映射到低维空间的同时，使得低维空间中各个维度上的数据所包含的信息量尽可能大，投影之后的各个变量即称为主成分。其计算过程如下。

　　对于由m个特征，n个样本组成的n行m列矩阵X=[X1，X2，…，Xm]，首先对每一个属性向量减去其均值进行去中心化，即x=xij-j

　　计算样本的散布矩阵为：S=X*(X*)T

　　随后对散布矩阵S进行特征分解，求得其特征值和特征向量。特征值越大则代表原始数据在该特征向量维度上的方差越大，即所包含的信息量越大。

　　按照特征值大小进行排序，取其中最大的l个特征值对应的特征向量wi即可组成投影矩阵W=[w1，w2，…，wl]。通过投影矩阵W即可将原始属性向量投影得到l维的低维向量。

　　2试验结果分析

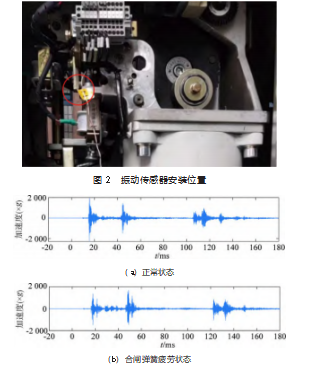
　　以LW30-126型SF6断路器为研究对象，该断路器采用CT30型弹簧操动机构。通过减少弹簧的预压缩量来模拟合闸弹簧疲劳故障，调大合闸电磁铁的间隙来设置合闸电磁铁铁心松动故障。选取压电式传感器测量振动信号，安装于弹操动机构的机构架上，如图2所示，采用胶粘与磁性底座相结合的安装方式。断路器在正常状态，合闸弹簧疲劳故障与合闸电磁铁铁心松动故障状态下各动作20次，测量合闸过程振动信号，获取了60组振动信号样本。3种状态下的典型合闸振动信号如图3所示。

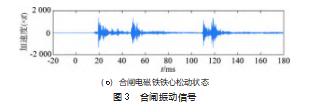
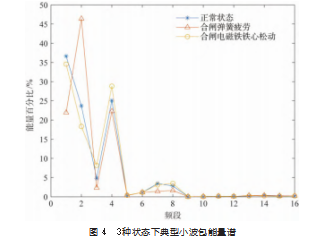
　　选取db1小波基函数，对振动信号进行5层小波包分解，得到32个频段，计算其能量谱。频段17~频段32的能量百分比接近于0，不能体现不同状态的差别，因此选择频段1~16的能量谱作为特征向量。断路器3种状态下的d典型小波包能量谱如图4所示。可见3种状态下断路器合闸振动信号的能量均主要分布在频段1-4。正常状态与合闸电磁铁铁心松动频段1能量占比最大，而合闸弹簧疲劳频段2能量占比最大。合闸弹簧为操动机构动作的能量来源，当合闸锁扣被解除后，由合闸弹簧的推动带动拉杆、凸轮、拐臂等一系列机构部件运动，而合闸弹簧疲劳会导致储能时存储的弹性势能减少，对合闸过程种的许多冲击振动事件均产生影响，因此对能量谱的影响程度最大。合闸电磁铁铁心松动会造成铁心冲撞合闸锁扣前的运动时间增加，铁心由在合闸线圈产生的电动力下加速时间更长，因此铁心撞杆撞击合闸锁扣的速度变快，能量变大。由于该撞击产生的振动较小，因此对能量谱的影响小于合闸弹簧疲劳故障。

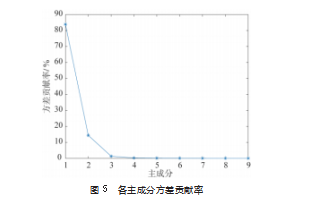
　　对60组样本，16维能量谱作为特征向量组成的样本数据进行主成分分析降维。计算得到9个主成分，计算每个主成分的方差贡献率与累积贡献率，如图5所示。主成分1与主成分2的方差贡献率分别为83.973 4%与14.357 1%，即主成分1与主成分2贡献了原始数据98%的信息量，因此将原始数据投影到主成分1与主成分2上进行后续的分析。

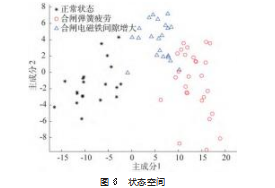
　　3种状态在主成分1与主成分2组成的状态空间中的分布如图6所示。可见，3种状态下断路器振动信号的小波包—能量谱主成分具有良好的可分性。正常状态、合闸电磁铁铁心松动与合闸弹簧疲劳对应主成分1分别主要分布在[-20，0]、[0，10]、[10，20]的区间内，对应主成分2分别主要分布在[-6，5]、[0，8]、[-10，5]的区间内。相比于主成分1，各状态主成分2的分布范围重叠更大，即主成分1对3种状态差异信息的刻画程度更大，蕴含的信息更多。

　　3基于SVM的故障诊断

　　支持向量机(Support Vector Machine，SVM)是由Vapnik提出的一种二分类的广义线性分类器。对于如图6所示的线性可分问题，令样本数据集为：

　　D={(%1,y 1),(%2,y2),…,(%n,yn)}

　　%i∈ℝm,yi∈{-1,+1}

　　寻求一个分类超平面，在满足将不同类别的样本正确分隔开的同时，使得每类样本中离该超平面最近的样本距离超平面尽可能远。分类超平面可以描述为：

　　ωT%+b=0(6)

　　式中：ω为法向量；b为超平面到原点距离。

　　要使得该超平面能够正确地分类两类样本数据，则需要满足：

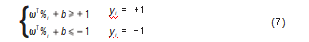
　　使得式(7)中不等式等号成立的样本数据称为支持向量，两类样本支持向量到分类超平面的距离之和为：

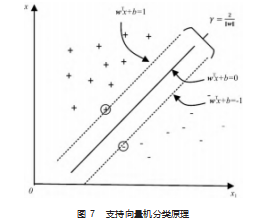
　　在满足式(7)的约束下，使得γ最大，即可找到最优的分类超平面。实际中许多问题都是线性不可分，因此需要通过核函数将样本数据映射到高维空间中，使得样本在高维空间中线性可分[19-22]。常用的核函数有高斯核函数、拉普拉斯核函数、多项式核函数等。同时，为了保证算法的鲁棒性和泛化性，往往允许在一部分样本上出现误分类，通过引入松弛变量与惩罚因子来对误分类进行约束。如图7所示。

　　采用SVM建立断路器正常状态、合闸弹簧故障状态与合闸电磁铁铁心松动的诊断模型。由于SVM针对二分类问题设计，为了实现断路器3种状态的分类，采用一对多法，针对每种状态建立一个SVM模型，训练时将该状态划分为一类，剩下的两种状态划分为另一类。以小波包能量谱主成分1与主成分2作为样本特征参数进行分类模型的建立。对于60组样本数据，正常状态、合闸弹簧故障状态与合闸电磁铁铁心松动3种类别标签分别记为1、2、3，每种状态下随机取出5个样本作为测试集，待模型建立完成后进行模型精度的验证，剩下的作为训练集对模型进行训练。训练完成后，输入测试集的样本数据进行类别预测，结果如图8所示。由图可知，所建立的SVM模型能够对断路器3种状态共15个样本进行准确分类，正确率为100%。

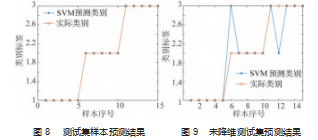
　　使用未降维前的小波包能量谱作为特征参数建立模型进行对比，预测结果如图9所示。合闸弹簧故障与合闸电磁铁铁心松动故障均出现了一个样本分类错误，测试集分类正确率为86.6%。可见，使用主成分分析对小波包能量谱降维后，模型分类的准确率提升，这是因为主成分分析降维时在没有丢失有效信息的前提下，去除了原始数据中的噪声和信息冗余的影响，从而提高了模型精度。

　　4结束语

　　本文通过计算合闸振动信号的小波包能量谱，使用主成分分析降维后，基于SVM建立了断路器正常状态、合闸弹簧疲劳与合闸电磁铁铁心松动故障3种状态的分类模型，从而可以实现对两种故障的识别诊断，得出结论如下。

　　(1)小波包-能量谱能够有效提取振动信号的能量特征，对断路器不同状态进行区分；

　　(2)主成分分析在降低特征向量维度的同时，未造成关键信息的丢失，去除了信息冗余，从而提高了分类模型的精度；

　　(3)基于SVM的故障诊断模型能够对正常状态、合闸弹簧疲劳与合闸电磁铁铁心松动故障3种状态的样本正确分类。

参考文献：

　　[1]杨韧,冯兴鲁,张家瑞,等.ZN63型断路器操动机构合闸弹簧应力松弛仿真分析与诊断[J].高压电器,2020,56(5):18-23.

　　[2]周国伟,董建新,肖珊珊,等.合闸弹簧疲劳状态下高压断路器弹簧操作机构应力分布及动力响应研究[J].高压电器,2019,55(10):44-51.

　　[3]刘超,赵伟涛,张强,等.真空断路器弹簧操动机构机械特性的仿真与优化[J].高压电器,2019,55(8):65-71.

　　[4]马速良,武建文,袁洋,等.多振动信息下的高压断路器机械故障随机森林融合诊断方法[J].电工技术学报,2020,35(S2):421-431.

　　[5]姚杨,林金涛,刘洪正,等.基于复合特征的断路器机械故障诊断方法研究[J].中国电机工程学报,2019,39(21):6439-6452.

　　[6]万书亭,豆龙江,李聪,等.基于VMD和样本熵的高压断路器故障特征提取及分类[J].振动与冲击,2018,37(20):32-38.

　　[7]关永刚,杨元威,钟建英,等.高压断路器机械故障诊断方法综述[J].高压电器,2018,54(7):10-19.

　　[8]黄辉敏,王飞风,苏毅,等.基于LMD和SVM的高压断路器弹簧操动机构状态异常检测方法研究[J].高压电器,2020,56(5):243-248.

　　[9]王强,王莉,沈进锐.基于多重分形与SVM的异步电动机轴承故障诊断[J].测控技术,2017,36(11):18-22.

　　[10]李斌,李爽,鲁旭臣.高压断路器机械特性振动信号特征提取和故障诊断方法研究[J].高压电器,2015,51(10):138-144.

　　[11]李宾宾,柯艳国,田宇,等.基于小波包理论的高压断路器机械状态检测[J].合肥工业大学学报(自然科学版),2019,42(7):924-929.

　　[12]盛程,王韵婷.自然循环条件下窄通道临界热流密度的小波分析[J].内蒙古电力技术,2022,40(1):88-91.

　　[13]孙来军,胡晓光,纪延超.改进的小波包-特征熵在高压断路器故障诊断中的应用[J].中国电机工程学报,2007(12):103-108.

　　[14]潘超,陈祥,蔡国伟,等.基于小波包尺度-能量占比的变压器三相不平衡绕组振动特征辨识[J].仪器仪表学报,2020,41(4):129-137.

　　[15]沈艳霞,周文晶,纪志成,等.基于小波包与SVM的风电变流器故障诊断[J].太阳能学报,2015,36(4):785-791.

　　[16]唐勇波,桂卫华,彭涛,等.PCA和KICA特征提取的变压器故障诊断模型[J].高电压技术,2014,40(2):557-563.

　　[17]杨启帆,段大卫,李楠,等.基于主成分分析的串联电池组故障诊断实用方法[J/OL].电力自动化设备:1-11[2022-07-19].

　　[18]李佳桐,张跃,符栋梁,等.发电机螺栓松动故障特征检测方法及试验研究[J].噪声与振动控制,2021,41(2):136-139.

　　[19]肖白,邢世亨,王茂春,等.基于改进KDE法和GA-SVM的多风电场聚合后输出功率长期波动特性预测方法[J].电力自动化设备,2022,42(2):77-84.

　　[20]邵阳,武建文,马速良,等.用于高压断路器机械故障诊断的AM-ReliefF特征选择下集成SVM方法[J].中国电机工程学报,2021,41(8):2890-2901.

　　[21]陈铁,吕长钦,张欣,等.基于KPCA-WPA-SVM的变压器故障诊断模型[J].电测与仪表,2021,58(4):158-164.

　　[22]孟杭,黄细霞,刘娟,等.结合随机森林和SVM的风机叶片结冰预测[J].电测与仪表,2020,57(17):66-71.