摘要：面对智能建筑、数字化城市对综合布线系统的需求，提出了一种基于多级并行蚁群算法的综合布线路径规划方法，并建立了数学模型，用于在满足约束条件下的最短路径寻优。寻优过程中将各设备之间的路径看成三维空间树，设备之间布线路径用曼哈顿距离衡量，各子系统布线最短路径就是以起始点设备为原点到多个终端信息点的最短路径和。以6层实训大楼某一工作区子系统为工程案例，进行仿真实验，数据结果表明算法平均达优率较高，鲁棒性指标较小，寻优过程稳定。针对6层78个工作区子系统的大数据综合布线项目，该多级并行寻优的蚁群算法同样能够在较短时间实现全局最优，收敛速度较快，寻优路径精准。

　　关键词：综合布线；路径规划；蚁群算法

　　Comprehensive Cabling Path Planning Based on Multi-level Parallel Ant Colony Algorithm

　　Liang Jiawei，Liu Xiangyong，Zhang Junqiang

　　(Zhongshan Technician College,Zhongshan,Guangdong 528400,China)

　　Abstract:The comprehensive cabling system is the foundation for the rapid development of intelligent buildings and digital cities.From the workspace subsystem to the building cluster subsystem,there are multiple optional wiring paths between any two devices in each link.Consider the paths between devices as a three-dimensional spatial tree,and measure the wiring path distance between devices using Manhattan distance.The optimal path for the workspace subsystem is the optimal tree from the router device to multiple information points.This article proposes a comprehensive wiring path planning method based on multi-level parallel ant colony algorithm and establishes a mathematical model for optimizing the shortest path under constraint conditions.The experimental simulation shows that the multi-level parallel optimization ant colony algorithm can achieve global optimization in a short time,with fast convergence speed and precise optimization path.

　　Key words:cabling system;path planning;ant colony algorithm

　　0引言

　　综合布线系统是智能建筑、数字化城市快速发展的基础和需求，没有综合布线技术的快速发展就没有智能建筑的普及和应用。随着智能楼宇迅速发展，如何在保证布线工艺前提下，确保布线线缆路径最短，成为综合布线工程设计的重要问题。

　　综合布线系统是建筑物或建筑群内的传输网络，是建筑物内的“信息高速路”，是用数据和通信电缆、光缆、各种软电缆及有关连接硬件构成的通用布线系统，能支持语音、数据、影像和其他控制信息技术的标准应用系统，为办公提供信息化、智能化的物质介质。包括建筑物内部弱电系统所有设备及设备之间、以及内部设备与外部线路的所有连接点的连接线缆和布线设施。按照《综合布线系统工程设计规范》(GB 50311—2016)，一般把综合布线系统工程分为7个部分：工作区子系统、水平子系统、垂直子系统、管理间子系统、设备间子系统、进线间子系统和建筑群子系统。

　　目前针对强电电缆敷设的研究较为成熟，可借鉴的方法较多。罗建国等[1]提出基于树状、网状搜索算法的电缆敷设设计与应用方法；朱翰超等[2]将Dijkstra算法应用于电力电缆敷设优化中；黄祖光等[3]同样提出了基于Dijkstra算法的电缆敷设系统设计，并给出实际案例；李治等[4]将遗传算法和改进的Dijkstra算法相结合，应用于电缆敷设优化设计中；杨亚伟等[5]提出一种改进的A*算法在电缆敷设设方法；鲍伟强[6]对基于蚁群优化算法的电缆敷设进行了深入研究。但是针对楼宇弱电系统综合布线最优路径规划研究还不多，研究还处于初级阶段。陈超等[7]提出基于遗传算法的综合布线路径布局方法，彭雪海[8]尝试将微粒群优化算法应用于高层建筑结构化综合布线系统，李凌[9]对于基于蚁群算法的高层建筑布线优化设计进行了深入研究。

　　楼宇综合布线路径经过7个子系统，在确保布线工艺(明敷)前提下，每个系统内的两个设备之间线缆都应实现最短路径，最终实现整个综合布线系统最短路径。本文提出一种基于带约束的多级(对应7个系统)并行蚁群算法的智能布线路径规划优化算法，能够相对准确找到每一个子系统内两设备之间的最短布线路径，使综合布线成本进一步降低。同时利用多级并行蚁群优化算法，使综合布线路径选择过程大大增速，从而提升设计过程时效性。

　　1综合布线路径规划模型分析

　　为方便综合布线路径规划分析，首先建立图1所示的空间三维坐标体系。布线空间中某施工点的定位用空间坐标为(x，y，z)，按照综合布线“横平竖直”工艺要求(明敷)，可以将综合布线规划路径分两步实施，首先沿着X轴和Y轴组成的平面网格进行布置，然后再进行Z轴网格路径规划，每一个网格均设定为边长为一个单位的正方体。在设计实施时，网格的密度可以根据施工现场的实际情况进行调节，以提升路径规划精度和效度。

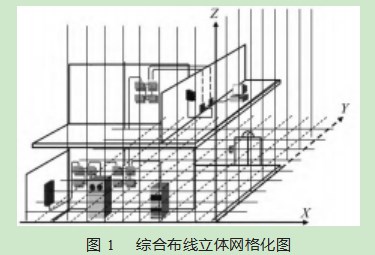
　　按照图1所示，在进行路径规划时，设备之间的线缆连接转化为单位立方体之间的路径选择。综合布线系统分为7个子系统，每个子系统内的布线是相对独立的，因此在布线路径规划时，可以从工作区子系统到建筑群子系统进行分级实施。每一级内线缆的拓扑结构一致，即树形结构，如图2所示。针对树形结构，要首先确定起始点的位置，将起始点位置坐标作为相对原点，然后根据施工图纸确定其余终端点位置坐标，同时将空间中线缆无法穿行的设备或立柱等作为障碍点，并列出其空间坐标。在所有空间点位置坐标确定后，即可以开展在约束条件下的综合布线路径规划[7]。

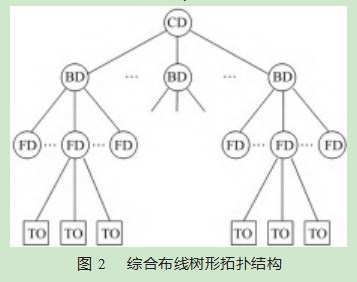
　　空间中任何两个节点之间的距离均有欧式距离和曼哈顿距离两种计算方法，两种计算方法的定义不同。假设立体空间内两点P 1、P2，坐标分别为P 1(x 1,y 1,z 1)、P2(x2,y2,z2)，欧式距离是指两个空间节点之间的实际距离，计算公式为：

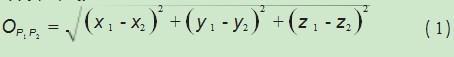
　　曼哈顿距离是指从规划为方型建筑区块的城市间最短的行车路径，车辆行驶过程中是无法穿越障碍物的。两点间的曼哈顿距离定义为：

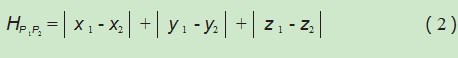
　　以上分析可知，在进行综合布线路径规划时，应选择两点之间的曼哈顿距离进行衡量。综合布线路径规划与传统的旅行商问题不尽相同，传统的旅行商问题是要求寻找一条经过所有点且每个点只被访问一次的最优路径，而综合布线路径规划中的每一条线路都是独立的，所以在进行最优选择时，要分别考虑每一个子系统内的每一条线路的路径。

　　假设一个子系统内起始点(机柜)的位置为P0(x0,y0,z0)，此子系统分别包含语音点(电话)、数据点(网络)、视频点(监控)等3类不同终端信息点。若任意一个语音点信息终端位置坐标为Ti(xi,yi,zi)，任意一个数据点信息终端位置坐标为Dj(xj,yj,zj)，任意一个视频点信息终端位置坐标为Vk(xk,yk,zk)。则综合布线路径规划优化问题转化为求最短路径：

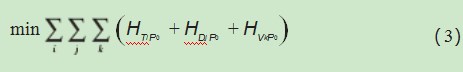
　　考虑到工程实际，3类信息点终端均属于弱电系统，可以共享布线路径，且共享路径越多，布线成本越低。因此，在进行路径优化时，应首先判断语音点、数据点、视频点等3类不同终端信息点的坐标，若出现坐标完全相同的信息点，则在点位数据栈中作减一处理。

　　2基于多级并行蚁群算法的综合布线路径规划

　　由于综合布线系统层级较多，产品种类丰富，整体结构较为复杂，需引入智能算法进行过程寻优。随着智能建筑出现，综合布线终端信息点呈几何增长，算法寻找的较优布线路径与理论最优布线路径将存在一定偏差。

　　2.1带约束的多级布线路径选配方法

　　根据《综合布线系统工程设计规范》(GB 50311—2016)规定，各段电缆长度按下列公式进行计算：

　　式中：C为工作区设备电缆、电信间跳线及设备电缆的总长度；H为水平电缆的长度，(H＋C)≤100 m；T为电信间内跳线和设备电缆长度；W为工作区设备电缆的长度；D为调整系数(0.2或0.5)。

　　线缆敷设于导管内，国标规定，布线导管或槽盒暗敷设于楼板时不应穿越机电设备基础，布线路由中每根暗管的转弯角不应多于2个。

　　在进行综合布线工程设计时，要满足以上约束条件。从工作区子系统到建筑群子系统整个链路中，每一段(共7段)链路中的任何两个设备之间都会有多个可选路径，且都会有一个在满足约束条件下的最短路径。找到7段中任何两个设备间的最短路径合并施工，就形成整个综合布线系统的最优路径。

　　以工作区子系统为例，如图3所示。假设工作区有N个信息点(TO)组成，则从路由器到各个信息点共需布线N条链路，每条链路均由n段可选路径，则此段链路一共包含N×n条可选路径。若某大楼共有C个这样的工作区，那么一共有C×N×n条路径供选择，其中应有一条路径为最优路径(即在满足约束条件下的最短路径)。对于一栋智能化大楼，N、n等数据相对较大，例如某30层的办公大楼，每一层约20间工作区，每间工作区平均15个信息点。同样在水平布线子系统等其余6个子系统中也有众多可选路径，且一个园区会有多幢办公大楼。那么布线路径组合方案呈级数倍增长，运算时间趋于极限，无法采用人工穷举寻找最短布线路径。本文提出一种基于带约束的改进蚁群算法的计算机辅助选优布线路径方法，能够较好地解决这一问题，模拟仿真数据表明该方法能达到理想效果。

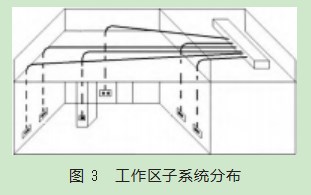
　　意大利学者Marco Dorigo于1992年首次提出蚁群优化算法用来寻找最优路径[8]。之后多位专家学者将蚁群算法用于计算机辅助选优过程，以提高施工质量、节约工程成本。

　　2.2综合布线解构造图建立

　　蚁群算法寻优时，蚂蚁释放的信息素可设定在路径上或节点上。在综合布线系统中，可以将设备、以及设备间的路径看成一棵三维空间树，工作区最优路径就是以路由器设备为起点到多个信息点的最优树。三维空间曼哈顿树距离树垂直投影在对应的二维水平面上的树最短时，空间曼哈顿距离树也是最短。

　　本文以设备之间的路径构造寻优模型，即蚂蚁信息素释放在路径上，设备作为寻优节点。此方法能够确保蚁群快速高效找出各设备之间的最短路径，输出一套较优的布线方案，从而降低项目综合布线成本。以工作区子系统寻优为例，笔者提出一种带约束的蚂蚁遍历寻优方法，将路径最短作为选配依据，将前述国标规定作为约束条件。依据前述，假设工作区有N个信息点(TO)组成，则从路由器到各个信息点共需布线N条链路，每条链路均由n段可选路径。设第j条链路的所有路径集合为Bjn，每只蚂蚁将从bjl指向bj(l+1)路径上进行单向寻优。设第j条链路最优路径编号为rj∈Rj，集合Rj表示N条链路的最优路径组合。

　　2.3蚁群算法路径规划数学模型

　　蚂蚁进行第j条链路遍历寻优时，在t时刻所有蚂蚁开始选择下一条路径，并在t+1时刻同时到达。定义蚁群算法的一次迭代表示在区间(t,t+1)内，由X只蚂蚁同时进行的X次移动，进行n次迭代后，蚁群中所有蚂蚁都进行一次完整遍历[10]。

　　为提升搜索速度，工作区N条链路采用并行搜索策略，每条链路释放的蚂蚁数量相同。定义M蚂蚁在t=0时从b0(工作区路由器)出发，每条链路上蚂蚁数量均匀分布，均为MN只。按遍历规则(路径最短)在各自链路上进行寻优，定义禁忌表R[X-1][n-1]，用于存储遍历到的路径编号。遍历结束，禁忌表中数据即为工作区最优布线路径链ο。在进行至第i步解构造时，蚂蚁x位于路径bij上，定义ο'=ο(j)为可行部分解，即已构造好的部分路径序列，蚂蚁在约束条件下将选择访问路径bij的可行邻域(见式(5))内的下一条路径bi(j+1)(bi(j+1)∈Bj+1)。

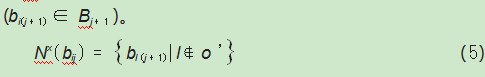
　　式中l∉ο'，为蚂蚁未访问的路径。

　　定义P(j+1)(t)表示蚂蚁x位于可行部分解ο'=ο(j)(在按约束条件下已构造好的部分路径序列)内，从节点bο(j)j行至bi(j+1)的概率为：

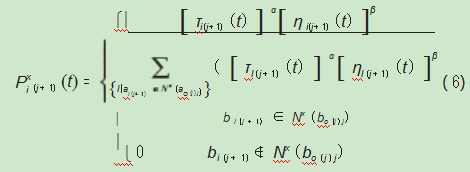
　　式中ηij(t)为基于问题的启发式信息，称之为能见度。

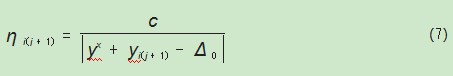
　　定义yx为此次迭代截至t时刻第m只蚂蚁遍历的全部路径计算出的y，即最小的传递函数；那么第m只蚂蚁在t+1时刻将要访问布线路径bi(j+1)(路径距离记为yi(j+1))；c为常数，数值在(0,1)间；在算法中规定若

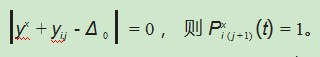
　　定义路径bij在t时刻的信息素浓度为τij(t)，代表第j个y在t时刻将要选择第i条布线路径的期望程度。

　　布线路径上的信息素余量系数用ρ表示；则从t到t+n时刻信息素挥发系数为1-ρ；Φ为常数；第x只蚂蚁从开始到t+n时刻的遍历长度yx=y，y代表第x只蚂蚁在t+n时刻将访问的布线路径。规定：若|yx-Δ0|=0，则Δτij x=1。

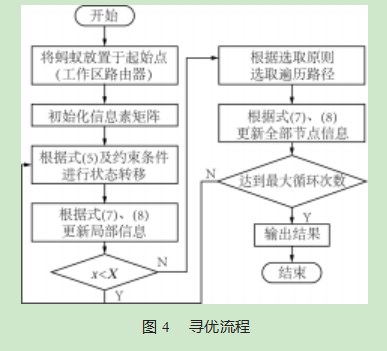
　　并行搜索策略的每一条链路算法寻优流程相同，如图4所示。经过n次迭代，算出yx值，代表每只蚂蚁在布线路径间遍历长度，找到最小的ys，并记录到数据栈中。重复迭代寻优过程，直至计数器达到NCmax(设定的最大值)，算法停止。综合布线系统包含7个子系统，每个子系统寻优解构造图和寻优流程相同，因此，在完成7级寻优后，形成完整综合布线最优路径。

　　3仿真测试与结果分析

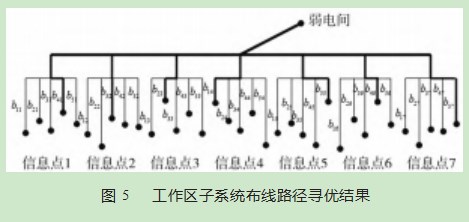
　　基于MATLAB软件进行仿真寻优过程实验，以某6层实训大楼为工程案例，大楼每层布局为1间办公室和12间一体化实训室，每层均设置1个弱电间。以第3层办公室工作区子系统为仿真实例，该办公室内需安装7个信息点位。在楼层空间网格化过程中，首先定位起始点(弱电间位置)坐标，弱电间位置一般在建筑设计阶段就已确定。然后再根据客户要求明确各类信息点终端的种类和数量。案例中7个信息点分别为语音点1个、信息点5个、视频点1个，工作区距弱电间水平距离为5m，该工作区为3.5 m×9 m×4 m房间。实际施工现场会存在多个障碍物，如立柱、通风管道等等，要先明确障碍物的空间位置坐标，并将其输入数据栈中。为加速寻优过程，提高寻优精准度，可以首先根据施工现场人为定义几条从起始点出发的可行路径，根据优化算法计算结果，精准确定终端信息点的坐标位置。假设本案例中从弱电间机柜上配线架(起始点)前往每一个信息点路径均有5条(长度不同)，如图5所示(该图仅为三维空间路径寻优展开示意图)。此项目N=7,n=5，设定最大循环次数NCmax=50，蚂蚁数量M=210开展并行寻优，每条链路上蚂蚁数量为30只。并行求解每条链路最优路径，如图5所示粗线部分路径(图中路径仅为通过三维空间寻优计算结果的示意)，找出最优的信息点安装位置。本次实验数据相对较小，蚁群算法不会陷入局部寻优，能快速搜索到最短路径。

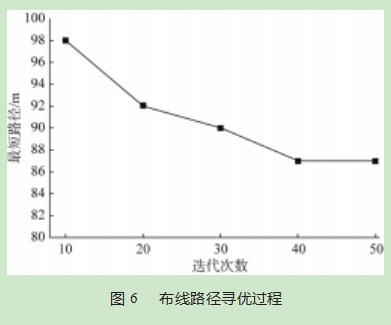
　　本文将实验进行并行扩展至30层楼，每层楼15个工作区子系统，同时完成7个子系统分级寻优，每个子系统内部进行并行寻优，寻优过程如图6所示，仅迭代约40次后找到最优解。结果表明，基于多级并行蚁群算法的综合布线路径规划方法能够较好寻找到整个项目的最短布线路径，节约布线过程中的材料成本和时间成本。其中平均达优率(指智能算法所有迭代所寻找到的最优解的均值与最优解目标值偏差绝对值与最优解的目标值之比，用以衡量算法的寻优过程的动态波动特性)ηave=92.37%；算法鲁棒性(算法所有迭代所寻找到的最优解的标准差与最优解目标值之比作为鲁棒性的判断指标)指标R=8.233×10-4，说明算法寻优过程稳定。

　　4结束语

　　综合布线系统是楼宇智能化的重要基础，是现代楼宇机电安装工程重要组成部分。本文建立了基于蚁群算法的综合布线路径规划数学模型，并且针对综合布线多个组成系统特点，构建出多级并行寻优流程，对蚁群优化算法进行改进。在综合布线系统集成设计之前，利用基于蚁群算法进行多级并行布线路径规划，精准规划综合布线线缆敷设路径，在约束条件下，寻找最短路径。实验仿真表明多级并行寻优的蚁群算法能够在较短时间实现全局最优，收敛速度较快，寻优路径精准。在人工智能技术飞速发展的今天，将智能优化算法应用于楼宇综合布线系统，能够极大提高综合布线的施工效率，降低施工成本。

　　[1]罗建国,韦思亮.基于树状、网状搜索算法的电缆敷设设计与应用[J].热力发电,2013,42(3):103-105.

　　[2]朱翰超,杜亚静,季节.Dijkstra算法在电力电缆敷设优化研究中的应用[J].电气应用,2014,33(24):115-118.

　　[3]黄祖光,朱安平,王凯,等.基于Dijkstra算法的电缆敷设系统设计及实现[J].电网与清洁能源,2020,36(6):105-110.

　　[4]李治,韩丹,任兴龙,等.基于遗传算法和改进的Dijkstra算法的电缆敷设优化研究[J].数学的实践与认识,2016,46(17):160-167.

　　[5]杨亚伟,王璐,王斐.一种改进的A*算法在电缆敷设设计中的应用[J].电线电缆,2016(3):32-35.

　　[6]鲍伟强.蚁群优化电缆敷设系统的研究[D].南宁:广西大学,2012.

　　[7]陈超,陈振中.基于遗传算法的综合布线路径布局研究[J].南京师范大学学报(工程技术版),2020,20(4):51-56.

　　[8]彭雪海.基于微粒群的高层建筑结构化综合布线系统[J].微型电脑应用,2023,39(2):164-168.

　　[9]李凌.基于蚁群算法的高层建筑布线优化设计和负荷计算[D].沈阳:沈阳工业大学,2007.

　　[10]DORIGO M,GAMBARDELLA L M.Ant colony system:a coop⁃erative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation,1997(1):53-66.

　　[11]DORIGO M,MANIEZZOV,COLORNI A.The ant system:opti⁃mization by a colony of cooperating agents[J].IEEE Transac⁃tions on SMC,1996,26(1):28-34.

　　[12]刘向勇.基于改进蚁群算法的液晶拼接屏选择装配[J].机电工程技术,2020,49(9):110-114.

　　[13]刘向勇,王鑫鹏.基于改进蚁群算法的单体电池选配技术研究[J].数学的实践与认识,2021,51(4):145-152.

　　[14]绳红强,黄海英,崔毅刚.基于A*蚁群融合算法的避障路径规划研究[J].机电工程技术,2022,51(7):45-49.

　　[15]霍非舟,高帅云,魏云飞,等.改进蚁群算法的拥堵环境疏散路径规划研究[J].计算机工程与应用,2023,59(11):263-271.