摘要：研究了一种有效的无人机稳定飞行姿态的方法。根据多旋翼无人机垂直、左右、前后运动和偏航运动的受力和运动原理，探索构建数学模型，选定合适的参考坐标系，选择四元数法用作描述四旋翼无人机姿态的数学方法，在描述多旋翼无人机的运动方式时，用横滚角、俯仰角和偏航角来验证关系，同时作为后续姿态控制的输入量。推理机体坐标系与导航坐标系两者互相转换时的变化矩阵，建立非线性动力模型，以互补滤波算法与扩展卡尔曼滤波算法为基础，将采集到的数据进行融合估算，结合串级PID控制器，以其作为框架，内部加上智能模糊控制理论，可以对PID参数的3个值Kp、Ki、Kd进行实时调节，使无人机具有更好的鲁棒性，当遇到突发情况时，飞控可以智能地调节参数，使无人机快速趋于稳定。采用MATLAB/Simulink仿真的结果表明，经过优化调节之后的模糊控制PID参数可以很好地调节无人机的姿态角速率和控制无人机的位置反应速率，提高无人机的稳定性。
       关键词：四旋翼无人机；坐标系；模糊PID；仿真模型

　　Abstract:An effective method for stabilizing the flight attitude of unmanned aerial vehicles(UAV)is studied.According to the force and motion principles of vertical,roll,pitch and yaw flight of quad rotor UAV,the mathematical model is established,the appropriate reference coordinate system is selected,the quaternion method is adopted as the carrier to describe the attitude of quad rotor UAV,and the relationship between quaternion and attitude Euler angle in the space coordinate system,namely roll angle,pitch angle and yaw angle,is constructed as the input of subsequent attitude control.The transformation matrix is inferred when the airframe coordinate system and navigation coordinate system are converted,a nonlinear dynamic model is established,combining the complementary filtering algorithm and the extended Kalman filtering algorithm to fuse and estimate the collected data,combining the cascade PID controller,taking it as the frame,and adding the intelligent fuzzy control theory internally,the three values Kp,Ki,Kd of the PID parameters can be adjusted in real time,In this way,the UAV can have better robustness,and the flight control system can intelligently change parameters according to the actual flight situation of the UAV to achieve fast and stable control.Simulations on MATLAB/Simulink show that the optimized fuzzy control PID parameters have good control ability for attitude angular rate of four rotor UAV and better position control for UAV.

　　Key words:UAV;coordinate system;fuzzy PID;simulation model

　　0引言

　　计算机技术和电脑运行速度的快速发展使得无人机的大脑——飞控系统也跟着进步。四旋翼无人机飞行的稳定性与其核心大脑——飞控有密切的关系，同时，它的飞行控制规律设计的质量也会影响无人机的飞行稳定性[1-3]。目前，四旋翼无人机的用途非常多，航拍、植保、测绘、巡检以及现在比较流行的无人机快递，因此对姿态稳定系统以及其他子系统都提出了更高的要求，结合现有的视觉技术开发、视觉定位与姿态稳定系统[4-8]，测量精度的提高有助于开发无线能量传输技术[9]，解决小型无人机的失控问题，同时多旋翼无人机的数学物理模型基本都是非线性的，而且还有一定的耦合性和气动不稳定性[10]，它的高精度控制问题囊括了当前控制问题中的各种难点，尤其是相对较难的视觉技术开发、视觉定位与姿态稳定系统，测量精度越高，无人机飞行的越不容易失控，也越容易操控[11]。本课题的研究意义在于，尽可能地寻找可以使无人机飞行过程中姿态稳定的方法，降低操作门槛，多旋翼无人机控制理论知识涵盖多学科、多方面，研究飞控问题可以为解决其他模型提供一定的理论参考价值[12]。越是姿态稳定的无人机，越可以帮助人们提高作业的效率，让人们不必担心作业过程中出现事故，有利于将多旋翼无人机普及到各行各业，有助于提高无人机产业的快速发展和壮大。

　　为了解决上述问题，本文旨在探索更有效的方法使得无人机的飞行姿态保持稳定，以四旋翼无人机为例，结合当前国内外无人机姿态控制的研究进展，结合卡尔曼滤波算法重构设计无人机姿态控制器，调节无人机在飞行过程中的稳定性和反应能力，然后建立数学模型推导控制函数，最后在MATLAB/Simulink工具箱中提取相应的功能模块来仿真运行，根据仿真结果理解各个控制参数对无人机飞行过程中姿态的影响，进而为整体设计无人机飞控打下基础。

　　1四旋翼无人机数学模型的建立

　　1.1建立坐标系

　　无人机的位置不确定，姿态容易偏移，导致研究无人机比较困难，需要用坐标系和数学模型辅助解决。数学模型的本质是把数学逻辑思路和数学语言结合起来的科学模型[12-15]。本文将四旋翼无人机作为重点研究对象，考虑其飞行原理为伯努利定律，运用假设方法，可视作具有严格对称结构的六自由度刚体，重心处于几何中心位置。刚体所受的重力也可以认为是沿着惯性坐标系Z轴负方向，相应的4个螺旋桨产生的拉力沿着本身的机体坐标系Z轴正方向，参考如下2个坐标系，如图1所示。

　　1.2建立数学模型

　　无人机的转动规律和直线规律直接影响模型的建立。要用无人机坐标系(Ob，Xb，Yb，Zb)和惯性坐标系(On，Xn，Yn，Zn)。常用的坐标系转换方法是角度旋转，也就是常见的欧拉角转换成四元数法，由于四元素法误差小，容易求解，所以四元数法在姿态解算中更有优势[16-17]。本文采用绕X轴运动的横滚角ϕ、绕Y轴运动的俯仰角θ以及绕Z轴运动的偏航角Ψ。参考刚体的基本属性，在不出现位移的情况下，坐标系的变换原理是通过对某个坐标系进行一定次序的旋转运动，与另一坐标系重合的过程。

　　式中：s为sin函数；c为cos函数；θ为无人机俯仰角；ϕ为无人机横滚角；Ψ为无人机偏航角。

　　2设计互补滤波器

　　根据前面的求导可得非线性的方程，然后需要结合无人机飞控里面的硬件设备陀螺仪、加速度计和数字罗盘。其中陀螺仪用于检测和计算四旋翼无人机的角速度，有了角速度值再计算飞行的角度值。偏差问题主要利用数学积分方法来解决。以时间为基数累计误差，误差累计到一定程度后会导致电路饱和，阻塞信号的传递，影响加速度计传感器和指南针传感器的工作。虽然加速度计传感器和指南针传感器在测量计算时不会产生累计误差，但是这两种参数的动态响应值小，设备反应慢。基于以上问题，根据3种传感器在频率范围内具有一定的互补性且相互独立，采用互补滤波器融合无人机飞行产生的数据的方法来校正累计误差，有利于提高测量精度和系统的动态性能。

　　采集到的飞行数据通过硬件处理。处理之后的数据有时会产生误差，所以需要再次利用滤波算法进行分析。常用的互补滤波算法存在一定的局限性，后来有研究提出了扩展卡尔曼互补滤波算法，本文分别分析两种算法得出来的数据，选用性能更好的算法，然后对无人机姿态和位置数据进行融合滤波操作，计算出无人机在各种飞行姿态下的较为准确的信息。

　　3智能模糊PID控制

　　3.1模糊PID控制原理

　　由于单回路PID可能会使系统输出产生瞬间剧烈的变化，为了避免多次整定参数的繁琐，设计了基于模糊规则的串级PID控制器，将模糊控制应用在了PID姿态控制中，经过数学建模、硬件处理数据，得到滤波之后的数据，就可以据此设计符合需求的串级PID控制器。最后通过MATLAB软件的Simulink工具箱来进行仿真实验验证。

　　首先基于模糊控制规则进行稳定性和抗干扰性运动。模糊化即基于一定清晰值的基础上，结合与其相关的模糊子集和下设包含关系的特定函数，进行整合得出模糊原则。模糊化需要推导出物理值和模糊值之间的相互关系，并根据二者之间的关系寻找模糊子集，综合子集各自的特点，尽可能地放弃缺点，最大化优点，并重新设计研发智能模糊串级PID控制器。然后需要重新进行抗干扰和稳定性仿真实验，导出智能模糊串级PID控制和普通串级PID控制器计算出来的数据，重新进行对比分析，确定哪种控制器对于无人机飞控的稳定性最有帮助，最能提高无人机的抗干扰能力。

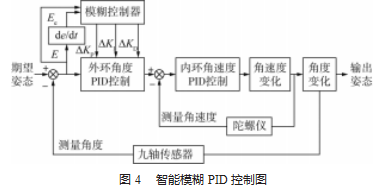
　　3.2模糊PID控制MATLAB仿真

　　利用前面推导出来的非线性模型的函数，调用MAT⁃LAB的Simulink工具箱，搭建模糊PID控制数模，再选择0-1的阶跃信号作为信号发生器。所用到的PID值如表1~2所示。

　　模型的精确度会对姿态角速度和位置产生很大影响，由于多旋翼无人机常见的运动方式有3种：俯仰前后运动、左右横滚运动以及偏航运动，给定姿态角速率为0 rad/s。初始位置x、y、z的3个坐标全部为0 m。仿真得到3个姿态角速率和位置的结果如图5~6所示。

　　从3种姿态运行结果来看，加入模糊控制规则PID值后，可以很好地调整无人机飞控工作过程中的几种运动模式下的角速率值，使其快速恢复稳态值，结果显示优化调节之后的模糊控制PID参数对四旋翼无人机的姿态角速率具有良好的控制能力。

　　从位置调节仿真结果可以看出，经过模糊控制PID参数的调整，X、Y和Z轴方向均达到了预期的稳态值。尽管个别位置出现微小的波动，但是由波动趋于稳定的速度有所提高，证明经过优化后的模糊控制PID参数对无人机的位置控制得比较好。

　　综上，加入模糊规则的逆控制器中各项参数物理论域和模糊论域之间的互相转化可以非常方便地进行量化因子的映射，量化因子的值在使用时需要按照各参数的特性进行取值。总之，模糊控制器利用修正量来修正模糊控制器中的控制规则，通过改变模糊控制器输出的角度值和位置值可以达到上面所述的效果，借鉴理想值响应曲线来修正模糊规则和隶属函数的合理化，以此原理逐渐提高飞控的稳定性。

　　4结束语

　　本文从经典串级PID控制入手研究了使用PID来进行无人机姿态控制的方法，根据无人机的工作原理选定合适的参考坐标系，基于四元数法解算数据，通过数学推导得出了机体坐标系与导航坐标系两者互相转换时的变化矩阵，建立非线性型数学模型，然后根据数学模型得出符合多旋翼无人机运动规律的动力相关模型。设计了基于模糊规则的串级PID控制器，将模糊控制应用在了PID姿态控制中，借鉴历史整定经验制定模糊规则，让无人机飞控能够智能地根据场景的变化来设置参数，自主调节，提高鲁棒性。

　　最后，利用MATLAB/Simulink工具箱仿真不同控制量变化对无人机的影响，针对经验制定的模糊规则的不准确性，对比理想输出与实际输出的偏差而构建模糊规则，通过学习不断改善模糊规则。仿真结果表明，控制结果合乎逻辑且优于经典串级PID，无人机受到干扰时可快速调整到之前的稳定状态，同时也有助于无人机提高响应速度、稳态精度，获得更好的抗干扰能力，进而为整体飞行控制系统的稳态设计打下基础。

参考文献：

　　[1]KONDAK K,BERNARD M,MEYER N,et al.Autonomously fly⁃ing VTOL-robots:modeling and control[C]//IEEE International Conference on Robotics&Automation,New York:IEEE,2007.

　　[2]段海滨,邱华鑫,陈琳,等.无人机自主集群技术研究展望[J].科技导报,2018,36(21):90-98.

　　[3]云超,李小民,郑宗贵.基于MATLAB/Simulink的硬件在回路无人机仿真系统设计[J].计算机测量与控制,2012,20(12):3306-3308.

　　[4]PATHIRANA P N,BISHOP A N,SAVKIN A V,et al.A robust set-valued state estimation approach to the problem of vision based SLAM for mobile robots[C]//2009 European Control Con⁃ference(ECC),August 23-26,2009,Budapest,Hungary.New York:IEEE,2015:2798-2803.

　　[5]HAN Z J,WANG P,YE Q X.Adaptive discriminative deep cor⁃relation filter for visual object tracking[J].IEEE Transactions on Circuits and Systems for Video Technology,2018:155-166.

　　[6]熊炯涛.基于单目视觉的微小型无人机自定位系统研究[D].广州:广东工业大学,2017.

　　[7]谭凯元,朱嘉林,邓君等.基于双目视觉的SLAM四旋翼无人机[J].机电工程技术,2022,51(9):83-87.

　　[8]阚亚雄.四旋翼无人机路径跟踪控制系统软硬件设计与实验研究[J].机电工程技术,2021,50(10):156-159.

　　[9]DEMARS C,ROGGEMANN M,WEBB A,et al.Target localiza⁃tion and tracking by fusing doppler differentials from cellular em⁃anations with a multi-spectral video tracker[J].Sensors,2018,18(11):3687.

　　[10]方可,杨明,李伟.无人机作业系统实验平台开发[J].实验技术与管理,2017,34(5):68-72.

　　[11]何乃晨.基于模糊自适应PID控制的四旋翼无人机飞控系统研究[D].天津:河北工业大学,20217.

　　[12]郭祖庆.小型四旋翼无人飞行器的控制算法研究[D].北京:北京理工大学,2016.

　　[13]荣辉,李冬,殷堂春.基于MATLAB无人机数学模型仿真分析与研究[J].科学技术与工程,2008,8(6):1510-1512.

　　[14]许景伟,余丽云.无人机四元数技术[J].电子产品可靠性与环境试验,2021,39(3):40-42.

　　[15]安朝,谢长川,孟杨,等.多体组合式无人机飞行力学稳定性分析及增稳控制研究[J].工程力学,2021,38(11):248-256.

　　[16]蔡朋成.基于STM32的四轴飞行器控制系统的研究与设计[D].淮南:安徽理工大学,2017.

　　[17]蒋钰,谌海云,岑汝平.基于四元数的四旋翼飞行器姿态解算算法[J].制造业自动化,2015,37(23):77-80.