摘要：为了改善松散回潮工序出口含水率控制精度低、水分波动大对香烟的生产带来的不利影响，采用Pearson相关性分析法筛选出松散回潮机出口含水率的主要影响因素，并将其作为模型的输入，然后基于现场生产数据驱动分别采用主元回归分析法、主元神经网络法以及BP神经网络法建立烟叶出口含水率的预测模型。基于某卷烟厂某牌号的生产数据对3种预测模型的预测控制效果进行检验，结果表明：3种模型含水率预测结果与实际值的平均绝对误差均在0.2%以内，主元神经网络预测模型输出结果与真实值的平均相对误差为0.81%，优于主元回归和BP神经网络预测模型。研究结果对于提高松散回潮工序烟叶出口含水率的控制精度有一定的指导意义。

　　关键词：数据驱动；松散回潮；出口水分；主元神经网络；BP神经网络；主元回归；预测模型

　　0引言

　　松散回潮工序的主要任务是对烟叶进行增温增湿，改善烟片的均匀松散度，提高烟片质量，满足后续制丝工艺要求[1]。水分是评价卷烟质量的一个重要指标，松散回潮过程的出口水分需要稳定的控制，以保证产品质量的稳定。然而，松散回潮本身是一个大时滞系统，受多种可测干扰和不可测干扰的影响，这些干扰因素通常又是相互耦合的[2-3]，因此，松散回潮的工艺质量控制极具挑战性。如何有效地优化松散回潮出口含水率控制过程，实现自动化工业控制是现阶段亟待解决的问题。

　　为了优化松散回潮的过程控制，许多研究学者提出了优化方法。欧阳江子等[4]提出了一种广义预测控制的优化方法，对松散回潮出口水分预测模型进行了滚动优化，使得出口含水率的稳定性得到了显著提高。董伟等[5]为松散回潮机设计了加水闭环系统，使用斜坡原理优化料头料尾的加水控制，提升了控制精度。吴硕等[6]通过将趋势控制与偏差控制相结合设计了“前加水为主，后加水调整”的加水系统，提升了松散回潮出口含水率的稳定性。汪钲轶等[7]提出了一种预测PI控制器，改善了松散回潮系统的滞后性所带来的影响。何毅等[8]采用梯度提升树法实现了对松散回潮出料含水率的预测，加入自学习能力提高了含水率的预测精度。以上研究在一定程度上改善了出口含水率的控制稳定性，但是，目前松散回潮出口水分控制系统中仍然存在着稳定性不高以及控制精度不足等问题。

　　本文基于对历史大数据的分析，对松散回潮出口水分控制系统进行优化改进，使用主元神经网络法、主元回归分析法以及BP神经网络法对出口水分进行预测控制优化，以期对提高松散回潮出口含水率控制稳定性和控制精度具有一定的参考价值。

　　1数据预处理

　　1.1样本数据

　　围绕松散回潮工序，以某卷烟厂TB-L松散回潮机为研究对象，采集生产某一牌号的卷烟对应的松散回潮工序数据53批，共计341 878条数据，参数包括入口含水率、出口水分设定、料头加水系数、加水量修正值、水流量、物料流量、松散润叶设定流量、生产用蒸汽流量、热蒸汽质量流量、热风温度、罩压力、出口含水率、松散润叶出口温度、烟叶牌号、批次等，数据采集时间间隔1 s。

　　1.2数据筛选对齐

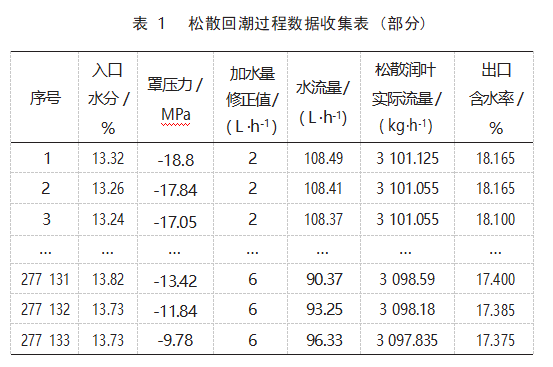
　　将直接采集到的原始数据按照时间排列。由于存在时滞，同一时刻采集到的数据的因果关系不匹配，为了准确研究松散回潮工艺整个过程对局部烟叶的加工效果，需要将各个位点采集的参数进行时间对齐。各变量的延时关系确定方案主要有：(1)通过绘制出各变量的曲线图，找到输入变量的突变信号，观察输出变量的响应时间，根据变量的开始、结束的时间窗进行观察与定位，确定各输入变量与输出变量即出口含水率之间的延时时间。(2)通过在生产现场实际观察与计时的方式，多次测量料头、料尾、带标记的中间料进出松散回潮设备的时间，确定关键变量平均延迟时间。综合使用以上方法进行多次测试，确定了烟叶从入口水分仪到加水点[9]、从加水点到出口水分仪，以及从入口水分仪到出口水分仪位置的平均用时分别是48、196、244 s，通过筛选有效数据，最后得到各变量对齐后有效的可分析样本如表1所示。

　　1.3数据分析

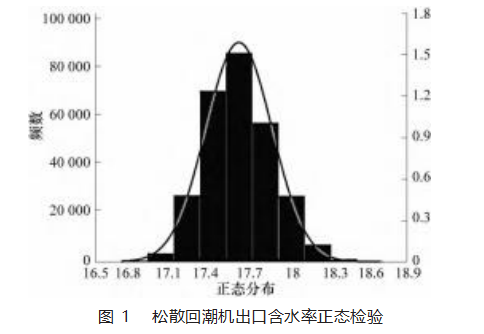
　　为保证数据分析的有效性和预测结果的准确性，需要对松散回潮机出口含水率进行正态检验[10]。经Kol‐mogorov–Smirnov检验后的松散回潮机出口含水率正态性检验直方图如图1所示。在0.05置信度下基本符合均值17.6%的正态分布。

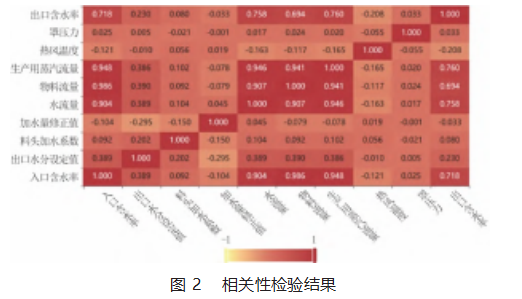
　　松散回潮出口含水率控制系统是一个典型的大滞后多变量控制系统，采用Pearson相关性检验法[11]对现场收集表中的数据进行相关性分析，确定关键影响因素，图2示出了各变量两两相关性分析结果。由图可知松散回潮机出口含水率的关键影响因素有：物料流量、入口含水率、生产用蒸汽流量、加水流量、出口水分设定值、热风温度。

　　1.4数据标准化

　　对出口水分进行预测建模时，由于各个变量的量纲不一致，为消除量纲差异的影响[12]，使用Z-score标准化公式计算得到的输入数据标准化值为：

　　2模型构建算法

　　2.1主元回归预测模型

　　通过上文数据分析确定了影响松散回潮出口含水率的主要影响变量，可通过主元回归分析法(Principal Component Regression Analysis，PCA)[13]得到控制系统的预测模型，解决多变量可能存在的共线问题。

　　主元分析法提取多维数据的主成分使变量降维[10]。首先选取分析样本中的一部分数据作为模型训练样本，形成一组输入输出样本矩阵，如输入矩阵为：

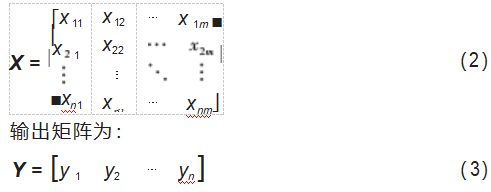
　　通过对这两组训练样本数据矩阵进行主成分计算、回归参数计算，得到Y关于X的主元回归模型。

　　2.1.1主成分计算

　　首先用标准化的样本数据矩阵计算各变量之间的相关性矩阵，输出变量Y和输入变量X之间的相关性系数矩阵表示如下：

　　式中k＜m。选定一个累计贡献率界定值，若前k个主成分的累计贡献率≥90%时，认为输入变量矩阵X的主要变化可以用X的前k个主元素解释。

　　根据主元分析方法，可以将输入矩阵X分解为m个主成分，如式(6)所示：

　　2.1.2建立主元回归模型

　　根据前文分析，用X降维后的k个主元素t 1，t2，⋯，tk进行回归分析，由此得到基于主成分的输出Y：

　　2.2 BP神经网络预测模型
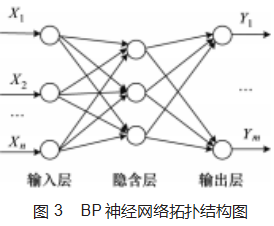
　　BP(Back Propagation)神经网络是20世纪80年代提出的一种多层前馈神经网络，拓扑结构如图3所示。由输入层(输入值X1，X2，…，Xn)、隐含层(调整权值ωij和ωjk)、输出层(得出预测值Y1，Y2，…，Ym)构成，BP神经网络的拓扑结构的计算功能非常强大，稳定性好，适用于大量数据的模型训练[14-16]。

　　BP神经网络的建模过程如图4所示。首先，根据上文的数据标准化公式对数据进行归一化处理，提升模型训练速度；其次，初始化BP神经网络拓扑结构层的神经元数，其中隐含层的确定尤为重要，可通过下面的公式来确定隐含层神经元数大致范围：

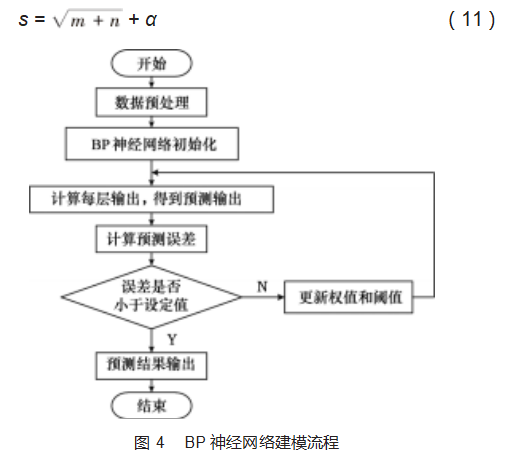
　　式中：m为输入层(input layer)神经元数；s为隐含层(hide layer)神经元数；n为输出层(output layer)神经元数；α为1~10之间的常数。然后，确定激活函数，激活函数f(x)的选取一般有logsig、tansig、purelin等形式，初始化权值、阈值，确定学习速率。最后，计算输出结果以及预测输出与期望输出之间的差值e，根据预测误差e更新权值和阈值，直至误差满足设定值，停止迭代。

　　3模型应用效果检验

　　3.1主元回归法预测效果检验

　　采用主元回归方法对松散回潮机的烟叶出口含水率进行预测，样本数据中80%作为训练样本、20%作为测试样本，以生产用蒸汽流量x1、热风温度x2、出口水分设定值x3、水流量x4、物料流量x5、烟叶入口含水率x6为输入变量，烟叶出口含水率为输出变量。为了得出最优的模型参数，分别训练得到如下3种参数模型：

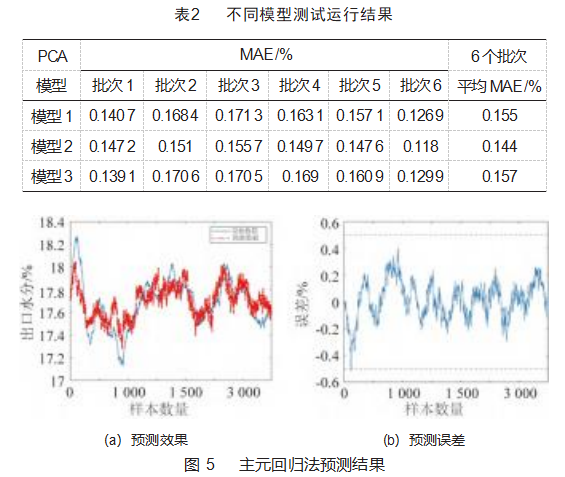
　　分别使用3种模型对测试数据的6个批次数据进行测试，结果如表2所示。表中MAE为预测的平均绝对误差，以每种模型6个批次的MAE平均值作为评价标准。从结果可知，模型2的平均MAE最小，说明预测效果最佳，因此选取模型2作为主元回归法的预测输出模型，对第51批次样本数据进行测试，预测结果如图5所示，预测曲线和实际出口含水率曲线吻合度较高。

　　3.2 BP神经网络预测效果检验

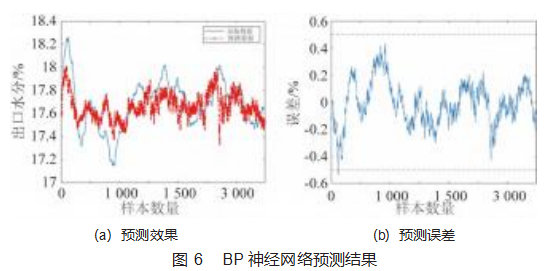
　　以松散回潮工序出口含水率的主要影响因素为输入，烟叶出口含水率为输出，设定训练次数1 000次，训练速度0.01，训练目标0.000 01，以purelin为训练传递函数，计算预测值与实际值的误差，采用梯度下降算法调整权重和阈值，建立6个神经元的输入层、7个神经元的隐含层以及1个神经元的输出层的BP神经网络模型。使用训练好的模型测试第51批次样本数据，测试结果如图6所示。

　　3.3主元神经网络预测效果检验

　　通过运用前文所述的主成分降维方法，首先建立松散回潮工艺参数的降维数学模型，并求出初始变量矩阵相关特征量，并计算累计贡献率，将已分析得到的参数变量降维至5个主成分，根据式(6)得到5个降维后的主成分数据。将BP神经网络的输入参数设为5，其余设置参数不变，训练得到主元神经网络模型。使用训练好的模型测试第51批次样本数据，测试结果如图7所示。

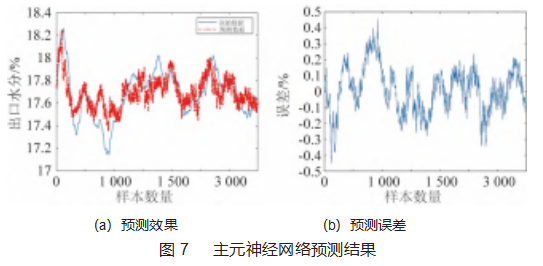
　　为了清晰明确地反映上述3种预测模型的预测精度，还需要计算2个重要的指标——平均相对误差(MRE)以及相对误差范围(RER)，其表征了目标参数预测模型预测值的偏离范围，越小说明偏离程度越低，预测跟踪效果越好，3种方法的预测结果平均值见表3。

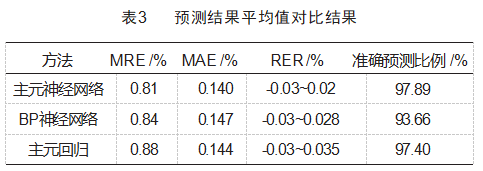
　　由表3可得：针对松散回潮这个具有多变量的系统，使用3种模型预测结果误差均控制在0.2%以内，能满足松散回潮出口含水率为(设定值±0.5%)工业生产允差要求；采用主元神经网络构建的预测模型与主元回归法相比，其预测精度得到了较大提升；同时将输入变量以主成分方法进行降维，相比于传统的BP神经网络进一步缩短训练网络所耗时间，提高预测模型运行效率。

　　3.4松散回潮出口含水率稳定性控制效果检验

　　本项目的目的是为了研究仿真预测模型用于指导实时控制的研究意义与价值，因此需要进一步做控制验证，使用统计分析方法提取一批历史有效稳定控制数据(出口含水率控制在(17.6±0.1)%范围内)，根据预测模型得到理论加水量计算模型，主元回归分析模型可直接根据公式获得理论及加水量控制模型，神经网络模型由于非显性考虑采用迭代逼近法来获取误差范围内的理想加水量。通过预测模型得到的理论加水量与实际人工操作稳定控制加水量进行对比验证，3种模型的控制效果验证如图8~10所示，其中主元神经网络的控制平均相对误差为0.01，BP神经网络为0.024，主元回归为0.06，由结果可知，以上建立的3种预测模型对于松散回潮出口含水率的稳定控制具有一定的效果。

　　4结论

　　根据Pearson相关性分析筛选出松散回潮机出口含水率的主要影响因素，将主元神经网络模型、主元回归分析模型和BP神经网络模型应用于松散回潮工序出口含水率的预测控制系统中。对3种预测模型的检验表明：3种模型出口含水率预测值与实际值的平均绝对误差均在0.2%以内，预测效果较优。采用主元神经网络构建的预测模型平均绝对误差和平均相对误差分别为0.14%和0.81%，控制效果验证的平均相对误差为0.01，控制精度提高58%~83%，其出口含水率预测精度和对加水量模型的控制效果验证都优于其他两种方法，使得松散回潮出口含水率更接近生产工艺设定值，对于达到松散回潮机烟叶出口含水率稳定控制的目标具有一定的指导意义。

　　参考文献：

　　[1]宋克强,韩利强,袁书豪.松散回潮机出口水分稳定性研究[J].中国高新技术企业,2013(1):27-19.

　　[2]HE Y,LI B,PU Y,et al.Uncertainty-aware data-driven tobacco loosening and conditioning process moisture prediction and con‐trol optimization[C]//2021 IEEE 10th Data Driven Control and Learning Systems Conference(DDCLS 2021),May 14-16 2021,Suzhou,China.New York:IEEE,2021:600–607.

　　[3]WANG Y,CHEN X F,PENG X Y,et al.An operation mode opti‐mization method for tobacco loosening and conditioning process based on batch clustering and KNN algorithm[J]//2018 Chinese Automation Congress,30 November-2 December 2018,Xi'an,China.Xi'an:CAC,2018,2:715-1430.

　　[4]欧阳江子,王东方,戚晓江,等.基于广义预测控制的松散回潮出口含水率控制系统[J].计算机测量与控制,2020.28(3):103-108.

　　[5]董伟,李坤,王健,等.HAUNI松散回潮滚筒含水率控制系统的改进[J].烟草科技,2012(11):20-25.

　　[6]吴硕,高卫,孙延钊,等.基于趋势与偏差控制的松散回潮机加水系统.[J].烟草科技,2020,53(6):108-112.

　　[7]汪钲轶,陈文先,金世益.基于预测PI控制器的松散回潮出口水分控制[J].设备管理与维修,2021,11.

　　[8]何毅,李斌,普轶,等.基于梯度提升树的烟草回潮机出料含水率预测[J].软件,2020,41(6):151-157.

　　[9]刘穗君,王玉芳,李超,等.基于统计回归分析的松散回潮出口含水率精准控制系统[J].烟草科技,2017,50(3):88-93.

　　[10]钟文焱,陈晓杜,马庆文,等.基于多因素分析的烘丝机入口含水率预测模型的建立与应用[J].烟草科技,2015,48(5):67-73.

　　[11]张文彤,邝春伟.SPSS统计分析基础教程[M].北京:高等教育出版社,2011.

　　[12]黄陈林,汤亚玲,张学锋,等.PCA和PSO-ELM在高炉铁水硅含量中的预测仿真[J].计算机仿真,2020,37(2):398-402.

　　[13]杨全振,苏成利.基于主元回归方法的多变量控制系统性能评估[J].化工自动化及仪表,2013,1(9):8-11.

　　[14]许明艳.基于ARIMA模型和BP神经网络模型的江苏省GDP预测分析[D].青岛:山东大学,2020.

　　[15]邱锡鹏.神经网络与深度学习[M].北京:机械工业出版社,2020.

　　[16]刘路.改进的BP神经网络在车辆目标识别中的应用研究[J].机电工程技术,2021,50(4):192-195.