摘要：卧式砂磨机在研磨时，被磨物料在分散盘与研磨内筒之间的间隙之间运动，通过与研磨介质、分散盘、研磨内筒之间产生高速的碰撞、挤压从而产生破碎。基于离散元法对砂磨机的研磨破碎颗粒过程进行数值仿真，讨论分散盘转速以及研磨介质球大小对破碎效率的影响，并进行正交试验和极差分析。经分析表明：转速对研磨破碎效果更大，随着转速上升，颗粒破碎效果也随之上升，但当转速达到一定的值后，其提升效果将不再明显；选用了几种不同的研磨介质球粒径，当粒径为4.5 mm时的表现最优。考虑到系统的稳定性以及加工成本，经过交叉试验得出最优参数为选取4.5 mm氧化锆珠球、分散盘转速600r/min，为提高卧式砂磨机生产效率提出一定的参考依据。

　　关键词：卧式砂磨机；破碎；颗粒替换；黏结模型

　　0引言

　　矿产资源一直是高需产品，卧式砂磨机作为磨矿的一种主要机型，是磨矿、冶金行业的重要核心装备，如何提高砂磨机的研磨效率已成为行业的研究热点。

　　21世纪初，许多学者围绕砂磨机的粉磨机理开展了大量的基础性研究工作[1-7]。随着仿真技术的发展，逐渐有学者将仿真技术应用到研磨领域。张国旺[8]通过计算流体力学(CFD)方法对螺旋式、棒销式以及盘式的搅拌磨机进行了数值模拟仿真，并通过试验验证了仿真结果的正确性。Tavares[9]提出一种DEM中基于球形的破损模拟模型。Jayasundara等[10]通过计算流体力学(CFD)和离散元法(DEM)的耦合模拟了Isamill磨机中不同研磨介质、载荷以及转速的影响，并通过正电子发射例子跟踪进行了验证。Kenawi[11]基于DEM方法的对立式搅拌磨进行了设计和运行参数的优化。张瑞新[12]运用离散元软件EDEM对双齿辊破碎机破碎效率进行仿真研究，考察了物料性质、物料粒度分布、齿辊转速等对其破碎效率的影响规律。通过有限元与离散元的建模仿真，许多学者对砂磨机的工作参数进行了优化，但未曾有将破碎模型引入砂磨机的仿真过程中，直观地察看砂磨机的破碎效率。

　　本文对现有的砂磨机进行分析，得到了主要参数及模型，利用离散元法对砂磨机工作进行数值模拟，引入颗粒替换模型来模拟颗粒破碎的过程，根据黏结键的断裂情况来比较不同工作参数的情况下，砂磨机的破碎效果。并最终通过正交分析，得出一组最优的工作参数，为优化砂磨机提供指导。

　　1建模与仿真分析

　　1.1颗粒定义以及参数设置

　　砂磨机的工作过程中主要有3部分参与：研磨腔及分散盘、研磨介质、被磨物料。砂磨机的材质为钢材，本次实验的被磨物料以二氧化硅颗粒为例，研磨介质为氧化锆珠。通体情况下都为类圆型，为了简化计算，在本文中将用圆形颗粒来模拟被磨物料以及研磨介质。研磨介质球根据实际情况选取粒径为5 mm的单球形颗粒，被磨物料初始物料粒径为8 mm，利用API二次开发，引入颗粒替换模型，用粒径为1.5 mm的颗粒通过黏结键黏结成团后替换掉8 mm的被磨物料颗粒。

　　定义各颗粒的物性参数。研磨介质材料为氧化锆，被磨物料材料为二氧化硅，砂磨机机体为钢材。三者自带的力学特征以及其三者之间的接触参数如表1~2所示。

　　1.2几何模型的设置

　　如图1(a)所示，砂磨机主要由研磨内筒、主轴、分散盘几部分构成主要工作空间。现有的砂磨机为8个分散盘均匀布置，为了简化计算，将利用对称原则，截取1/4段工作区间来进行数值模拟分析。由于离散元软件对实体建模的功能并不强大，故首先在Solidworks中对砂磨机的简化模型进行建模，通过转化为.Stl文件导入至离散元软件中。得到简化模型如图1(b)所示。

　　1.3全局设置

　　在前处理界面中对颗粒的接触模型进行设置，在Physics标签下设置颗粒与几何模型之间的接触模型选取无滑移的Hertz-Mindlin模型[13]，颗粒对颗粒之间额外增加一个bonding黏结模型，同时需要在Geometries标签下的PliginFactories体积力模型从外部导入ParticleReplac‐ment.API，该API为颗粒替换的关键，要使该API正常运行，需提前将大颗粒与小颗粒之间的相互坐标提前定义好。通过新建一个仿真文件，采用大颗粒包裹小颗粒，直到小颗粒填充满大颗粒内部并稳定下来后，再将小颗粒坐标信息导出，写入颗粒替换API中。获取颗粒替换坐标信息如图2所示。

　　1.4黏结模型简介

　　在离散元法中，颗粒替换主要有单球体以及重叠球体两种方式[14]，本文选用的是单球体方式，即颗粒之间将通过“黏结键”连接起来，黏结键可承受切向以及法向力，当达到其极限应力时，颗粒间的黏结键会断开，颗粒黏结键断开后，颗粒之间则按照Hertz-Mindlin模型来求解。当黏结键未断裂时，颗粒之间的相互作用力根据下列公式[15]进行更新。

　　式中：J为圆截面的极惯性力矩；RB为黏结键的黏结半径；M(t)、M(t)分别为当前t时刻切向方向黏结力矩和法向方向黏结力矩；F(t)、F(t)分别为当前t时刻切向方向黏结力和法向方向黏结力；K、K分别为黏结键的切向刚度和法向刚度；Δθs、Δθn分别为切向方向角位移增量和法向方向角位移增量；Δus、Δun分别为切向位移增量以及法向位移增量。

　　当模型中采用bonding黏结模型时，相互黏结时会同时存在颗粒之间的接触应力以及黏结键产生的黏结力，接触力由Hertz-Mindlin模型来求解，而颗粒之间的黏结力则取决于颗粒材料的最大法向应力以及最大切向应力，可根据圆截面的拉压、扭转以及弯曲应力公式推导出。

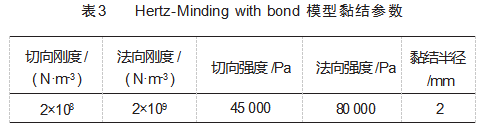
　　为了使颗粒间能够成功黏结，黏结半径应比颗粒的实际接触半径大，一般要大20%左右。选取硅砂bonding参数如表3所示。

　　1.5仿真过程

　　颗粒替换是由小颗粒替换成大颗粒，再由小颗粒黏结成小颗粒团体。黏结过程时间很短，若仿真时间步长过大，则会使颗粒没有黏结成功，时间步长是迭代计算之间的时间量，固定的时间步长是在瑞利步长的5%~40%之间，本文将时间步长设置在5%，以保证颗粒替换能够正常进行，总仿真时间设置为12 s。网格大小的设置，网格大小直接关系着仿真的速度，本文选取最小颗粒的3倍大小。仿真开始立即静态生成50个8 mm二氧化硅颗粒。生成被磨物料后，设置颗粒替换时间在仿真开始0.01 s时，此时大颗粒完全生成且未与机构发生接触，研磨介质也未生成，不会影响替换过程。在0.015 s时加入研磨介质球颗粒，且分散盘开始转动。仿真12 s后，在后处理板块查看其黏结键的断裂情况。颗粒破碎仿真过程如图3所示。

　　2仿真实验

　　2.1实验设计

　　砂磨机在工作过程中，研磨筒静止不动，分散盘高速转动带动研磨介质和被磨物料相互运动，使得物料颗粒在三者之间碰撞、摩擦后破碎。研磨介质球大小以及分散盘的转速是影响颗粒破碎的关键性因素。因此优化研磨介质球大小以及分散盘的转速n。采用单因素变量法，设置两组实验，通过分析仿真后颗粒间的黏结键存留数对破碎效果进行对比。

　　(1)变换分散盘转速，分析其对砂磨机破碎效果的影响。分散盘与研磨筒内壁宽100 mm。分散盘之间间距为80 mm，分别仿真分散盘转速为200、300、400、500、600、1 000 r/min时的颗粒破碎情况，通过数值模拟仿真得到的黏结键保留数情况如图4所示。

　　(2)改变研磨介质球粒径，探究其对砂磨机研磨破碎的影响，分别设立研磨介质粒径为3.5 mm、4 mm、4.5 mm、5 mm、5.5 mm的研磨介质球颗粒工厂，选取氧化锆为研磨介质材料，分散盘转速为200 r/min，仿真时间12 s。材料参数设置以及仿真结果如表4、图5所示。

　　2.2仿真结果分析

　　由图5可知，黏结键的破裂速度随着分散盘转速增大而增大，随着分散盘转速的上升，黏结键的断裂个数也会增多，研磨破碎效果更好。但由图4可以看出，当转速上升到600 r/min后，黏结键的破碎效果将没有明显的提升。而转速与砂磨机的功率息息相关，在保证研磨效果的同时达到最低的功率是追求的目标；同时随着转速的上升，砂磨机主轴的振动也会随之增加，在保证研磨效果的同时使主轴的振动最小也是必要的。故综合以上两点因素，该砂磨机应选择600 r/min的转速更为合适。

　　从第二组的实验来看，在分散盘转速为200 r/min、研磨介质球材料为氧化锆时，研磨介质球粒径大小对被磨物料黏结键的破碎效果如图5所示，随着粒径的增大，当粒径在4.5 mm时，其黏结键的破碎效果取得最优值。经过观察与分析，介质球粒径越小时，同一时间能加速的颗粒数目就会相对而言增多，但是相互之间的碰撞能却在减小。介质球粒径越大时，颗粒加速的能量就需要的越多，同等转速下，能达到的速度将会变低。介质球粒径在4.5 mm时，颗粒间的相互碰撞动能大，加速过程充分。相对而言破碎效果最好。

　　3正交实验

　　通过单因素控制变量法选择出最佳工艺参数只能提供一定的参考性，具有很大的局限性，所以为了更加全面的分析砂磨机的工作参数对其研磨破碎效果的影响，通过正交实验来进一步考察，建立两因素、三水平的正交实验，正交水平表如表5所示。

　　根据图4~5可知，在已建立的正交因素表内，当转速选取800 r/min时，黏结键断裂效果最好，同理可知，选取颗粒粒径4.5 mm作为研磨介质球粒径时效果最好。通过对每一个因素进行平均极差分析可知，转速对砂磨机粉碎效果影响大，研磨介质球粒径次之。

　　通过上列3组仿真实验可知，转速对研磨效果的影响相较于研磨介质的影响更大，故选型时转速为主要的考虑因素，考虑到系统的稳定性问题以及加工成本，可选择转速为600 r/min，研磨介质球的粒径为4.5 mm。

　　4结束语

　　本文在现有的砂磨机机型上，通过Solid works对其建模，并使用离散元单元法，通过API二次开发功能，引进颗粒替换模型，实验由大颗粒破碎成小颗粒物料的破碎过程。并通过正交试验得出该卧式砂磨机的高效研磨参数。

　　(1)卧式砂磨机的研磨效率与研磨介质球的粒径息经过观察与分析，介质球粒径越小时，同一时间能加速的颗粒数目就会相对而言增多，但是相互之间的碰撞能却在减小。介质球粒径越大时，颗粒加速的能量就需要的越多，同等转速下，能达到的速度将会变低。介质球粒径在4.5 mm时，颗粒间的相互碰撞动能大，加速过程充分。相对而言破碎效果最好。

　　(2)砂磨机的研磨效率随着分散盘转速的增加会变高，但转速达到一定的大小后，提升的效果将不再明显。通过正交实验得到最优参数，最终选取转速为600 r/min，研磨介质球粒径为4.5 mm较为合适。

　　参考文献：

　　[1]林胜.我国超细粉碎设备的现状与展望[J].中国粉体技术,2016,22(2):78-81.

　　[2]张国旺,赵湘,肖骁,等.大型立磨机研发及其在金属矿山选矿中的应用[J].有色金属(选矿部分),2013(S1):191-194.

　　[3]王洋,高鹏,于光涛,等.搅拌磨机在弓长岭选矿厂细磨作业中的应用[J].现代矿业,2020,36(5):140-142.

　　[4]李艳军,郭旺,王绍兴,等.搅拌磨与球磨磨矿对比试验[J].东北大学学报(自然科学版),2017,38(4):562-565.

　　[5]丁浩,邢锋.矿物粉体搅拌磨湿法超细磨矿中研磨介质的行为与作用[J].中国粉体技术,2000(4):9-12.

　　[6]刘佳鹏,卢世杰,何建成,等.GJM型搅拌磨机的优化及其在石墨行业中的应用[J].有色金属(选矿部分),2017(1):69-73.

　　[7]Rhymer D,IngramA,SadlerK,et al.A discrete element method investigation within vertical stirred milling:Changing the grind‐ing media restitution and sliding friction coefficients[J].Powder Technology,2022,410:117825.

　　[8]张国旺,黄圣生.超细搅拌磨机的流场模拟和应用[J].矿山机械,2008,36(21):78-83.

　　[9]Tavares L M,Rodriguez V A,Sousani M,et al.An effective sphere-based model for breakage simulation in DEM[J].Powder Technology,2021,392:473-488.

　　[10]Yang R Y,Jayasundara C T,Yu A B,et al.DEM simulation of the flow of grinding media in IsaMill[J].Minerals Engineering,2006,19(10):984-994.

　　[11]Kenawi M A.Optimization of design and operation parameters of vertical stirred mill using DEM approach[D].University of British Columbia,2020.

　　[12]张瑞新,刘煜,郑群飞,等.基于EDEM的双齿辊破碎机破碎效率影响因素仿真分析[J].金属矿山,2018(2):154-159.

　　[13]文愿运,刘马林,刘荣正,等.颗粒离散单元法数值模拟与典型实验对比研究[J].中国粉体技术,2015,21(3):1-5.

　　[14]岳翔,李梓豪,马阳,等.EDEM_DEM模拟技术在矿石碎磨中的研究进展[J].金属矿山,2022(6):150-159.

　　[15]刘磊,高伟,廖泽楚,等.基于离散元法的高压辊磨破碎仿真研究[J].湘潭大学自然科学学报,2017,39(2):76-80.