摘要：管道腐蚀问题已经成为影响我国原油输配安全的重要影响因素，管道内检测是进行腐蚀泄漏风险预防的重要方法之一，但测量结果可靠性较低，一般腐蚀缺陷最大深度的可靠度仅为80%。为获得更高可靠度的腐蚀缺陷深度预测结果，需对检测数据进行进一步分析。以某原油长输管道为例，利用威布尔统计方法对各管段内腐蚀和外腐蚀的内检测数据进行统计建模，并采用3σ法则，提出了可利用内检测数据统计模型中0.999概率所对应的腐蚀缺陷深度值合理预测某一管段腐蚀缺陷极限深度的方法，通过该方法预测的腐蚀缺陷极限深度值可满足安全性要求，同时又可避免预测结果过于保守。利用3σ法则还能实现各管段腐蚀异常点位的精确识别。实践表明所提方法具有足够的可靠性，可为长输管道的安全风险管理提供理论支撑。

　　关键词：内检验；威布尔分布；长输管道；腐蚀异常

　　0引言

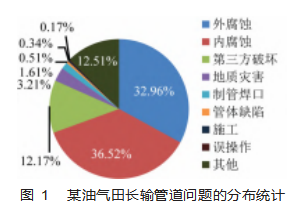
　　管道作为一种廉价高效的能源运输方式，被世界各国所普遍采用，发达国家则比例达到能源总运输能力的约70%[1-3]。我国截至2015年底，仅长输管线干线长度已超过10×104 km[4-5]，其中大多数为埋设管道，受土壤腐蚀、杂散电流和运送介质腐蚀等多种因素影响，管道本体遭受腐蚀破坏，使用寿命明显降低[6-8]，根据不完全统计，长输管道事故中约有30%~40%由腐蚀引发[9]，其中，美国因腐蚀造成的事故占18.3%以上[10-11]，俄罗斯因腐蚀诱发的事故占33%以上，欧洲管道因腐蚀造成的事故占24%以上，而在中国，部分企业因腐蚀发生的泄漏问题则占70%左右，如图1所示。

　　对于长输管道的腐蚀风险管理，最普遍的风险评估方法是Kent管道风险评估模型[12]，该方法主要用于长输管道的定性风险识别，并不涉及腐蚀风险的精细化管理，因此，对于管道腐蚀的精细化识别通常采用内检测方法[13]。其中，最为常用的是漏磁检测技术，该技术对于传感器与金属管道之间的提离距离不敏感，可在一定提离距离范围内检测处腐蚀缺陷[14]，因而更加适应长输管道可能存在的周向几何形变、局部形变等约束条件。同时，漏磁信号与腐蚀缺陷的体积相关，在等直径缺陷下，与缺陷深度线性相关[15]，并且对于裂纹缺陷，当缺陷与检测扫描方向的夹角小于一定角度时，漏磁也能同时识别表面和埋藏裂纹缺陷，且漏磁信号幅值与裂纹深度、长度和埋深均呈现线性关系[16]，便于定量分析缺陷几何尺度，但该检测技术所获得的腐蚀数据可靠度仅为80%，存在腐蚀深度预测值偏低，诱发腐蚀泄漏的风险，为此，有学者尝试用贝叶斯、极值分布等方法预测更加安全的腐蚀深度和剩余寿命[17]。

　　本文在前人的研究基础上，针对长输管道腐蚀缺陷的漏磁检测数据开展统计分析，利用威布尔分布作为腐蚀缺陷深度极值预测模型，提出了可利用内检测数据统计模型中0.999概率所对应的腐蚀缺陷深度值合理预测某一管段腐蚀缺陷极限深度的方法，构建更加安全可靠的长输管道腐蚀缺陷定量预测方法，并利用3σ法则推断管段内是否存在腐蚀速率较快的腐蚀异常点位，为长输管道腐蚀风险控制提供数据化支持。

　　1长输管道腐蚀缺陷深度极值预测模型

　　一般认为，极值分布理论主要用来分析随机事件中的小概率事件，且如果随机事件中各随机变量独立且同分布，若其底分布函数已知，则可求出极值分布函数，主要分为I型、II型和III型分布函数，其中III型函数为双参数威布尔分布[18]，通过对实际数据的验证分析，该型极值分布函数对于某一采样数据区间内的最大数据抽取比较优异[19]。为此，本文采用双参数威布尔分布进行管道缺陷深度数据的极值预测，如式(1)所示：

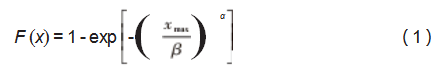
　　式中：F(x)为腐蚀缺陷深度取得极值xmax的概率；xmax为某一区域内腐蚀缺陷深度的最大值，mm；α为威布尔分布的形状参数；β为威布尔分布的尺度参数。

　　对式(1)两侧取两次对数，如式(2)所示：

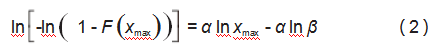
　　从式(2)可以看出，若将lnx与ln[-ln(1-F(x))]之间呈现线性关系，拟合系数分别为α和-αlnβ，因此可以通过线性拟合参数得到参数α和β，从而构建长输管道某一区域内的腐蚀深度极值及其安全可靠度的预测模型。

　　同时，考虑到漏磁检测精度一般为±10%的壁厚，实际检测的腐蚀缺陷深度往往是一个区间，因此，在数据处理时，将腐蚀缺陷深度的区间中值作为该部位的内腐蚀缺陷深度。

　　2算例分析

　　2.1被采样长输管道概况

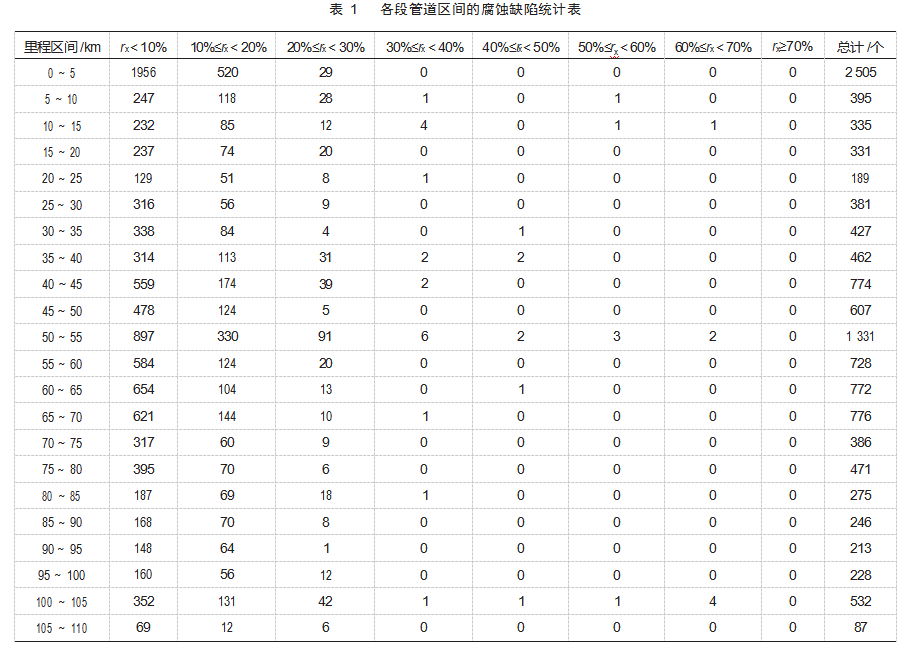
　　我国华南地区某原油管线，管道长度为105 670 m，设计压力5.0 MPa，工作压力3.5 MPa，设计温度为常温，管道规格为Ф529×7.0，材质为16 Mn。以5 000 m为一个区段，对该管道进行漏磁检测，金属损失程度rx的统计结果如表1所示。

　　2.2长输管道内腐蚀与外腐蚀差异性分析

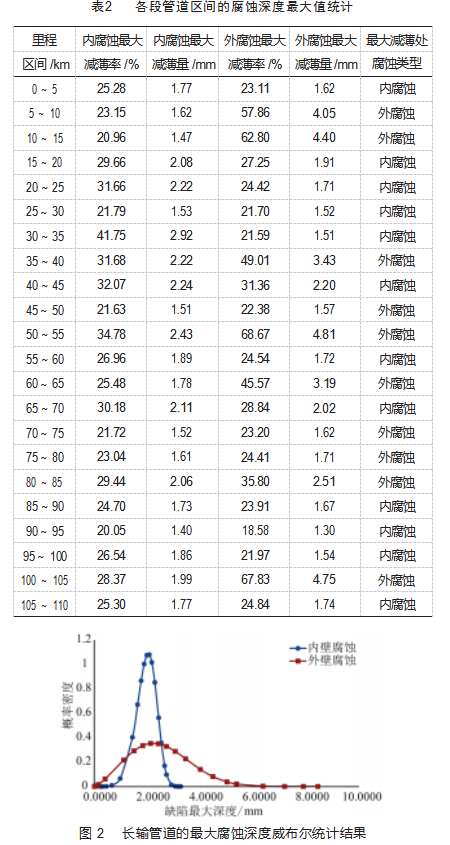
　　各区段内腐蚀和外腐蚀的最大减薄率如表2所示，其中最大减薄部位既有内腐蚀也有外腐蚀，分别对内外腐蚀进行威布尔统计模型分析，得到的统计结果如图2所示。从图中可以看出，内腐蚀和外腐蚀在最大缺陷深度的统计分布存在较大差异，通过t检验可以得知内腐蚀和外腐蚀最大缺陷深度存在显著差异的概率为97.56%，按照大于95%即可认为二者存在显著性差异，因此该长输管道内腐蚀和外腐蚀在泄漏威胁方面存在明显差异，需要分别分析。本文选择5~10 km里程内的管段腐蚀缺陷数据分别进行内腐蚀和外腐蚀最大缺陷深度的预测模型研究。

　　2.3长输管道内腐蚀极限损伤程度预测方法

　　根据5~10 km管段内腐蚀检测数据，利用式(1)~(2)得到该管段内腐蚀的威布尔统计模型如式(3)所示。而该管段内腐蚀缺陷深度的均值μ=0.902 4 mm，偏差σ=0.331 9 mm。

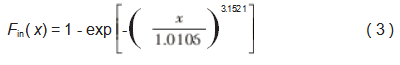
　　式中：Fin(x)为内腐蚀缺陷深度取得极值x的概率。

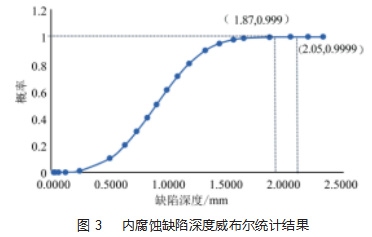
　　式(3)所对应的概率曲线如图3所示，按照3σ法则，当缺陷深度大于µ+3σ的时候，可以认为该缺陷深度与统计规律的随机影响无关，而可能是发生了局部腐蚀异常。因此，从统计学上可以认为µ+3σ是该统计分布影响下，腐蚀求缺陷深度的极限值，对于5~10 km的管段为1.898 1 mm，介于0.999~0.999 9概率所对应的腐蚀缺陷深度之间，更接近0.999概率所对应的1.87 mm，如图所示。同时，考虑到该管段的最大缺陷深度约为1.62 mm，如表2所示，因此，最终选取0.999概率所对应的1.87 mm作为内腐蚀缺陷预测极限值更为合理。

　　2.4长输管道外腐蚀极限损伤程度分析方法

　　根据5~10 km管段内腐蚀检测数据，利用式(1)~(2)得到该管段内腐蚀的威布尔统计模型如式(4)所示。而该管段外腐蚀缺陷深度的均值µ=0.714 8 mm，偏差σ=0.331 9 mm。

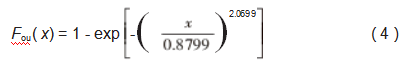
　　式中：Fou(x)为外腐蚀缺陷深度取得极值x的概率。

　　式(4)所对应的概率曲线如图4所示，与内腐蚀相同，按照3σ法则，对于5~10 km的管段外腐蚀缺陷，µ+3σ为2.059 6 mm，如表2所示的外腐蚀最大值为4.05 mm，明显高于2.059 6 mm的理论极限值，说明对于该管段外腐蚀缺陷存在局部腐蚀异常，通过对该点位开挖验证，如图5所示，该点位存在明显的外包覆层破损问题，证明3σ法则对于腐蚀异常点位识别的有效性。

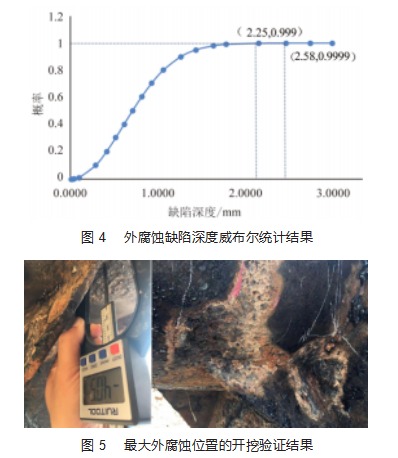
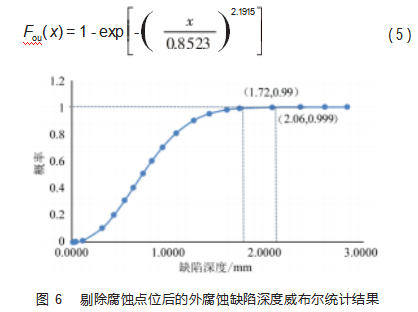
　　因此，剔除发生腐蚀异常点位的检测数据，重新对该管段外腐蚀统计规律进行分析，得到威布尔统计模型如式(5)所示。剔除腐蚀异常点后，该管段外腐蚀最大缺陷深度为1.975 6 mm，且外腐蚀缺陷深度的均值µ=0.694 0 mm，偏差σ=0.379 6 mm，按照3σ法则该管段外腐蚀理论极限值应为1.833 0 mm。式(5)所对应的概率曲线如图6所示，该曲线显示缺陷深度既大于实测最大深度1.975 6 mm，又大于3σ法则所推断的理论极限值的合理预测深度为0.999概率所对应的2.06 mm缺陷深度，因此可将该值作为外腐蚀缺陷预测极限深度值。

　　2.5基于漏磁内检测数据的长输管道腐蚀极限损伤程度评估方法讨论

　　首先，从表1和表2可以看出，对于一般的长输管道而言，通常的腐蚀行为可区分为内腐蚀和外腐蚀，二者对于我国长输管道的泄漏影响程度比较接近，如图1所示，并且内腐蚀和外腐蚀对于同一管段的安全威胁程度通常不从属于同一统计规律，且可能存在较大差异，如图3和图4所示，因此，对于长输管道而言，区分内腐蚀和外腐蚀的统计规律对于精细化控制管道泄漏风险十分必要。

　　其次，针对内腐蚀或者外腐蚀问题单独讨论，无论内腐蚀或者外腐蚀在某一管段内部可能存在不同的腐蚀机理分布，比如内腐蚀局部低点的垢下腐蚀，或者外腐蚀局部包覆层破损处的腐蚀等，这些腐蚀数据由于腐蚀机理与附近管段存在较大差异，将其数据与附近管段数据放在一起分析会得到错误分析结论，从而引发不必要的腐蚀泄漏风险或者过渡维修。并且，通常情况下，这类局部腐蚀异常往往腐蚀损伤程度更高，更加合理的风险控制手段是局部开挖修复，因此，对于这些腐蚀异常点位的有效识别更加重要，采用威布尔统计模型并结合3σ法则可以有效识别这类需要进行紧急维修的局部点位，可以避免盲目开挖带来的高附加值维修成本。

　　最后，对于内腐蚀或者外腐蚀极限损伤程度的预测，并非越保守越好，过于保守的估计会增加管道维护和运行成本，最合理的腐蚀极限损伤程度应该既略大于漏磁内检测的最大值，同时又要避免过大，通过对一段管段的内检测数据进行威布尔建模分析，发现基于内检测数据建立威布尔统计模型后，取概率0.999所对应的腐蚀缺陷深度值作为极限预测值更为合理，用该值作为腐蚀泄漏风险控制值，其可靠度高达0.999，且对应的缺陷深度值同时满足略大于漏磁内检测最大值和最接近满足3σ法则，瞒住统计意义上的安全性和经济性的双重优化。

　　3结束语

　　长输管道的腐蚀缺陷检测，以内检测为主，主要采用漏磁技术进行全面内检测，其检测数据可靠度一般为80%，为此，存在实际腐蚀缺陷深度数据大于检测数据的可能性，为此，本文以威布尔分布为方法对一条原油输配管道的内腐蚀和外腐蚀缺陷内检测数据进行腐蚀缺陷深度极值分析，用以避免管道内检测数据偏小可能导致的管道泄漏风险，并得出以下结论。

　　(1)对于原油长输管道，内腐蚀和外腐蚀由于腐蚀机理等方面的原因，其腐蚀深度数据不同属于一种统计规律，在进行数据分析时，需要加以区分。

　　(2)对于某一段原油长输管道，无论内腐蚀还是外腐蚀，均可利用威布尔分布建立统计分布模型，并利用模型中概率为0.999时的缺陷深度数据，合理预测该管段内腐蚀或外腐蚀缺陷的极限深度。

　　(3)对于某一段原油长输管道，无论内腐蚀还是外腐蚀，均可利用威布尔模型建立的统计分布模型，以及3σ法则，推断该管段内是否存在腐蚀速率较快的腐蚀异常点位，并得到了验证。

　　参考文献：

　　[1]张圣柱.南京丙烯管道爆燃事故探讨我国地下管道存在的安全问题[J].中国安全生产科学技术,2011,7(2):46-49.

　　[2]潘一,孙林,杨双春,等.国内外管道腐蚀与防护研究进展[J].腐蚀科学与防护技术,2014,26(1):77-80.

　　[3]毛节华,许惠龙.对我国埋地金属管道腐蚀的现状及原因分析[J].化工管理,2015,27(2):135-138.

　　[4]姜睿.我国"十二五"时期油气需求预测研究[J].经济问题探索,2012,12(1):7-13.

　　[5]李晓宇,王长友,刘玉文."十三五"期间中国天然气行业竞争态势及对策[J].天然气工业,2016,36(2):119-124.

　　[6]陈思维,覃明友,刘德绪,等.高含硫气田湿气集输管道冲蚀风险预测研究[J].天然气与石油,2015,33(1):80-84.

　　[7]薛振辛,自世武,冯斌.国内外输管道标准法规比较手册[M].北京:中国标准出版社,2008.

　　[8]冯先强,吕高稳,吕海燕,等.东营站内输油管道腐蚀与防护[J].石油化工腐蚀与防护,2007(6):24-25.

　　[9]王玉梅,郭书平.国外天然气管道事故分析[J].油气储运,2000,19(7),5-10.

　　[10]帅健.美国油气管道事故及其启示[J].油气储运,2010,29(11):806-809.

　　[11]周建新,吴轩,郭再富.美国管道事故对我国油气管道安全的启示[J].中国安全生产科学技术,2014(9):73-78.

　　[12]Kent Muhlbauer W.Pipe Risk Management Manual 2 second Edition[M].Houston:Gulf Publishing Company,1996[13]GB/T 27699-2011,钢质管道内检测技术规范标准[S].

　　[14]唐健,王荣彪,康宜华.大提离漏磁无损检测方法[J].无损检测,2022,44(4):67-72

　　[15]苏林,马雪莉,崔德荣,等.基于周向励磁的管道缺陷漏磁信号仿真分析[J].电焊机,2022,52(3):20-28

　　[16]王志军,陈洪恩,何曼如,等.裂纹缺陷定量漏磁检测数值模拟和实验研究[J].机械,2021,48(增):6-10.

　　[17]齐盛,帅健,顾强.基于贝叶斯和极值分析的原油储罐底板剩余寿命预测[J].中国安全生产科学技术,2021,17(增1):67-73.

　　[18]杨莉,胡国兵.基于Gumbel分布拟合检验的BPSK/QPSK信号调制识别算法[J].金陵科技学院学报,2021,37(2):46-52.

　　[19]宋晓猛,张建云,孔凡哲.基于极值理论的北京市极端降水概率分布研究[J].中国科学:技术科学,2018,48(6):630-650.