摘要：在永磁同步电机电流环PI调节的矢量控制系统中，udref和uqref尚不能真正实现对d-q轴电流的解耦控制，且由于逆变器的非线性和电机参数的时变性，使得相电流通常存在多种干扰，其表征为电流的谐波。首先建立了永磁同步电机在逆变器的非线性和电机参数的时变性下的实际模型；其次，分析了逆变器非线性及参数时变性的具体扰动模型；最后，提出一种扰动观测器，根据电机d-q轴电压方程，观测耦合项和扰动项，并对其补偿，以实现电流解耦及谐波抑制。通过对提出的扰动观测器的分析，说明了该方法电流解耦及谐波抑制机理，同时也给出了观测器的参数选取和稳定性证明。结果表明加入扰动观测器，实现了d-q轴电流的解耦，并使得A相电流的THD减小了16%，5次和7次谐波分别减小了26%和17%，验证了所提扰动观测器的电流解耦及谐波抑制效果。

　　关键词：永磁同步电机；扰动观测器；谐波抑制；电压补偿；电流解耦

　　Current Harmonic Suppression Method of Permanent Magnet Synchronous Motor Based on Disturbance Observer

　　Liu Xiaojun，Hung Tiyun，Zhang Hongman

　　(College of Transport Management,Nanjing Vocational Institute of Transport Technology,Nanjing 211100,China)

　　Abstract:In the vector control system of permanent magnet synchronous motor current loop PI regulation,udref and uqref can not really realize the decoupling control of d-q axis current.Due to the nonlinearity of inverter and the time-varying of motor parameters,there are usually many kinds of disturbances in phase current,which are characterized by current harmonics.Firstly,the practical model of permanent magnet synchronous motor was established under the nonlinearity of inverter and the time-varying of motor parameters.Secondly,the specific disturbance model of inverter nonlinearity and time-varying parameters was analyzed.Finally,a disturbance observer was proposed.According to the d-q axis voltage equation of the motor,the voltage disturbance term and coupling term were observed and compensated to suppress all kinds of current harmonics.By analyzing the proposed disturbance observer,the current decoupling and harmonic suppression mechanism of this method were explained,and also the parameter selection and stability proof of the observer were given.The results show that by adding the disturbance observer,the decoupling of d-q axis current is realized,and the THD of phase A current is reduced by 16%,and the 5th and 7th harmonics are reduced by 26%and 17%respectively.The current decoupling and harmonic suppression effect of the proposed disturbance observer is verified.

　　Key words:permanent magnet synchronous motor;disturbance observer;harmonic suppression;voltage compensation;current decoupling

　　0引言

　　随着电力电子技术和现代控制理论的发展，永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)被广泛推广应用在新能源汽车及城市轨道交通领域。PMSM具有效率高、功率密度高等诸多优点，且随着永磁同步电机及其驱动技术的发展，其在新能源汽车及城市轨道交通列车上有着极为广阔的前景。

　　永磁同步电机的控制方法多数采用矢量控制，在矢量控制中d-q轴电流是互相耦合的，耦合会对控制器的性能产生比较大的危害。且永磁同步电机的驱动通常采用三相逆变器，逆变器的非线性、死区时间、电流采样误差等因素，会导致电机电流产生谐波。同时，在永磁同步电机驱动中，由于电机运行会产生温度，温度使得电机的参数会发生变换，参数的时变影响了控制系统的精度。

　　以上的因素给永磁同步电机的相电流带来了干扰项，这些干扰项在电流中通常表征为谐波，这会对整个永磁同步电机驱动系统产生危害，比如影响了驱动系统的稳定性和可靠性，同时也给逆变器带来了额外的功耗[1]。因此，需研究永磁同步电机在逆变器非线性及参数时变性下的实际模型，在此基础上，需分析逆变器非线性及参数时变性的具体扰动模型，在实际模型和扰动模型基础上，需研究如何消除或抑制扰动项，这对提高电机的可靠性和稳定性以及降低逆变器的功耗有着重要意义。

　　永磁同步电机的电流谐波抑制方法有许多种，其多数从控制角度出发，通常是利用补偿算法。目前在该领域所提的方法主要有谐波电压补偿[1-7]、重复控制[8]、比列谐振控制[9]、自适应控制[10]、死区时间补偿[11]等。文献[1]中采用了比例谐振型自抗扰控制器来解决d-q轴电流耦合及谐波抑制，然而其参数较多，整定复杂。文献[2-3]提出了一种逆变器非线性因素直接提取的方法，以此电压补偿，但是其实现过程步骤较多。文献[4-7]分别采用了扰动观测器、滑膜观测器、卡尔曼滤波器和谐波观测器来进行电压补偿，以此来实现电流的谐波抑制，取得较好的效果。文献[8]采用了重复控制抑制指定频率的谐波，但该方法遇到谐波频率变化时需要重新设计控制器。文献[9-10]分别采用了比例谐振控制器和自适应陷波器的方法通过提取电流谐波分量，而后补偿至电压，但自适应陷波器的迭代时间过长。文献[11]通过直接计算死区时间，而后补偿至SVPWM的调制时间中，但其计算过程较为复杂。

　　针对d-q轴电压耦合情况，通常基于前馈型的电压解耦单元，其原理是根据定子电压方程的旋转电压添加了电压解耦单元[12]，由d-q轴电流环的PI调节器得到的d-q轴电压给定，再经过电压解耦处理后得到真正的d-q轴电压给定。

　　随着现代控制理论的发展，在处理复杂未知的实际工程中，观测器是一种较好的方法。在永磁同步电机驱动系统中，由于电机本体结构、逆变器的死区时间、电流采样误差等因素，会导致电机电流产生谐波，实质上就相当于外部干扰，通过设计扰动观测器观测出等效干扰，在控制中引入等量的补偿，实现对干扰完全抑制，从而达到电流谐波抑制的效果。

　　本文针对永磁同步电机控制系统中d-q轴电流耦合、逆变器非线性及参数时变等扰动引起的电流谐波问题，首先建立了永磁同步电机在逆变器的非线性和电机参数的时变性下的实际模型；其次，分析了逆变器非线性及参数时变性的具体扰动模型；最后提出了一种基于扰动观测器的永磁同步电机电流解耦及谐波抑制策略。本文从电机的d-q轴电压方程出发，推导出一种扰动观测器的模型，将观测的耦合项和扰动项补偿至d-q轴电压，以实现对电流解耦及谐波的抑制。通过分析所提出的扰动观测器，给出了系统的参数选取依据和稳定性证明。最后通过MATLAB/Simulink的仿真建模验证，验证了本文对电流解耦及谐波的抑制有效性。

　　1电机模型及电流谐波分析

　　1.1电机电流耦合性

　　图1所示为永磁同步电机基于PI控制的矢量控制系统拓扑图，d-q轴电流环存在互相耦合的情况，PI调节器不能完全消除这种耦合情况，转速的值越大这个耦合项就越大。同时，对于外界的干扰项d，容易引起电流的谐波。

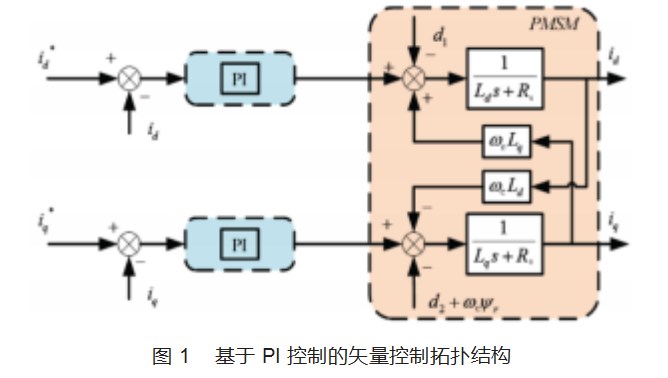
　　1.2逆变器非线性

　　在电机实际运行过程中，三相电压源逆变器的非线性、死区时间、电流采样误差等因素，使得逆变器输出电压波形发生畸变，文献[13]给出了结论：

　　在正常情况下，电机的绕组使用星形连接，因此3次以及3的整数倍次谐波会被消除。根据幅值判断，将5次和7次谐波分量作为主要研究对象。此外，5次和7次谐波经过Clark和Park变换后，在d-q轴坐标系会形成6次谐波。

　　另外，对于电机本体设计的非理想化因素也会导致d-q轴下的6次谐波。

　　1.3考虑参数时变的实际模型

　　考虑到逆变器非线性导致电压的畸变，在d-q轴坐标系下，永磁同步电机的电压方程可以表示为：

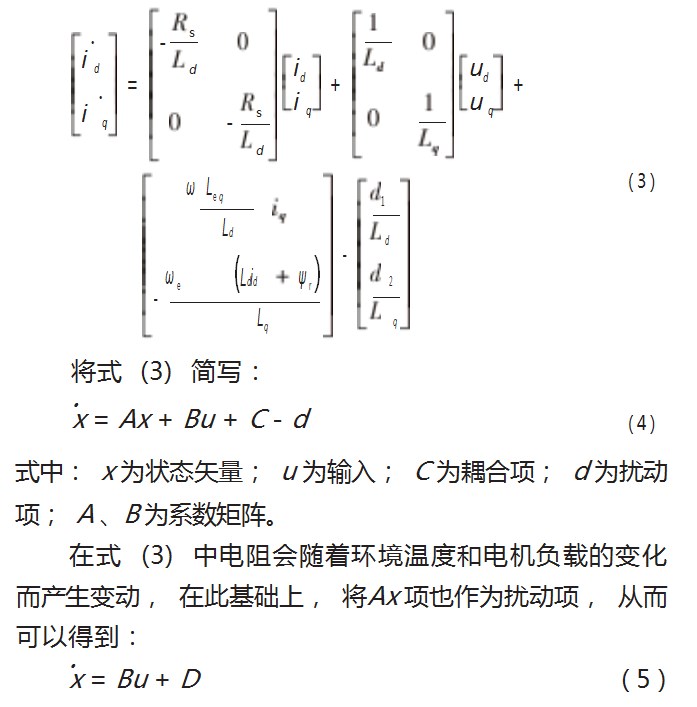
　　其中，D包括了耦合项和扰动项，且扰动项包括了逆变器非线性和参数时变。

　　2扰动观测器

　　2.1工作原理

　　由式(5)可知扰动项可表示为：

　　2.2稳定性分析

　　式(9)构建的扰动观测器方程实质上以M为状态量，构建M的观测值和实际值之间的误差为：

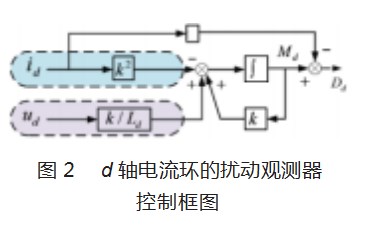
　　2.3 d-q轴扰动观测器设计及参数分析

　　以d轴电流环为例，设计扰动观测器，q轴与之类似。根据图2的观测器，可以得到d轴的扰动项Dd，这其中包括了耦合性和扰动项，因此在设计电流环调节器时，可以直接使用线性控制器，从而避免使用PI调节器，这样可以得到基于扰动观测器的d-q轴电流控制系统拓扑，其中速度环的控制仍采用传统PI控制器。如图3所示。其中，kp为线性控制器的增益。

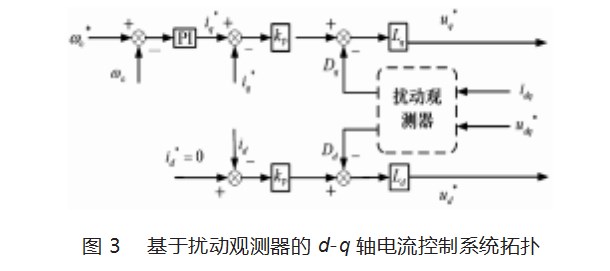
　　再者是电机的数学模型。由于本节的研究对象是d-q轴电流，因此选用d-q轴下的数学模型，以d轴数学模型为例，文献[14]给出：

　　本节将通过H(s)的伯德图来进行参数k和kp的分析。

　　图5给出了H(s)随各参数变换的伯德图。在图中，设置kp=10，增大k=-50、-40、-30、-20、-10。在低频段和高频段，随着k的减小，系统对扰动的抑制效果有明显增加。在频率等于100 rad/s周围，随着k的减小，系统的抑制效果并没有明显的改变。

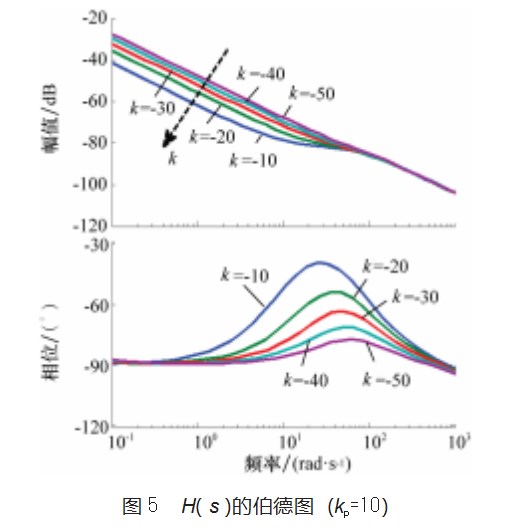
　　图6给出了H(s)随各参数变换的伯德图。在图中，设置k=1，增大kp=10、20、30、40、50。在低频段、中频段和高频段，随着kp的增大，系统的抑制效果有着明显的增加。

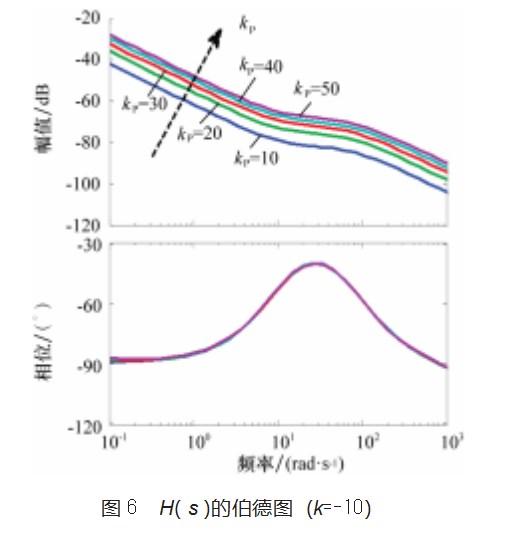
　　理论上当控制器的带宽增大时，系统的动态性能提高，但同时电流的纹波也会变大，因此参数选择要折中考虑。根据图5和图6可以发现，可以将k和kp相互关联：kp=-k。

　　3仿真分析

　　本文在MATLAB/Simulink中搭建表贴式永磁同步电机矢量控制模型，验证了在逆变器死区时间影响的电流谐波，接着为验证本文所提方法的有效性，在d-q轴电流环中加入所提扰动观测器补偿模块，从而活动仿真验证。相关参数如表1~2所示。

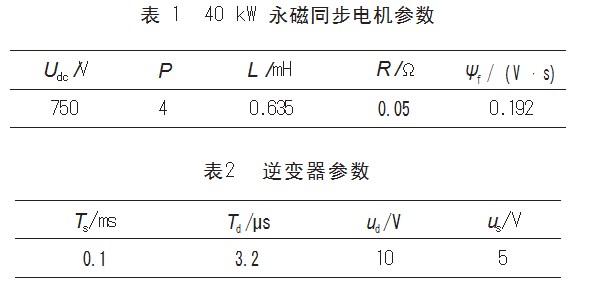
　　本文仿真条件：给定速度为150 rad/s。负载转矩开始给定为50 N·m，在0.15 s时，突加至120 N·m。对于本文的仿真结果如下。

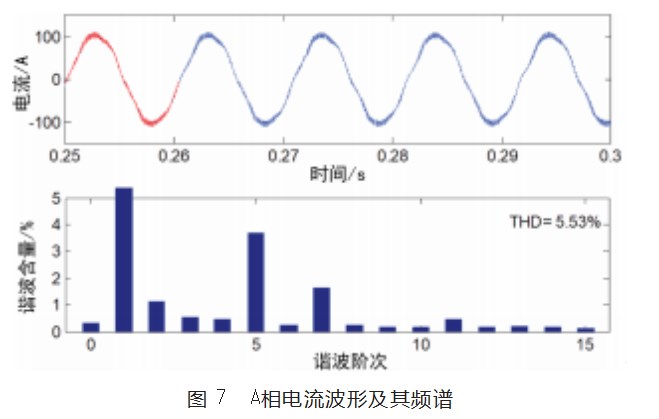
　　从图7可以看出，A相电流波形在过零点和峰值处有明显的畸变，正弦度不够，这是因为由于逆变器的而死区时间引起的5次和7次谐波。从频谱图可以得出，A相电流的5次和7次谐波分量突出，分别为3.71%和1.63%，THD=5.53%，这充分说明了由于逆变器死区时间而引起的电流谐波。

　　加入扰动观测器并补偿后的仿真结果如下。

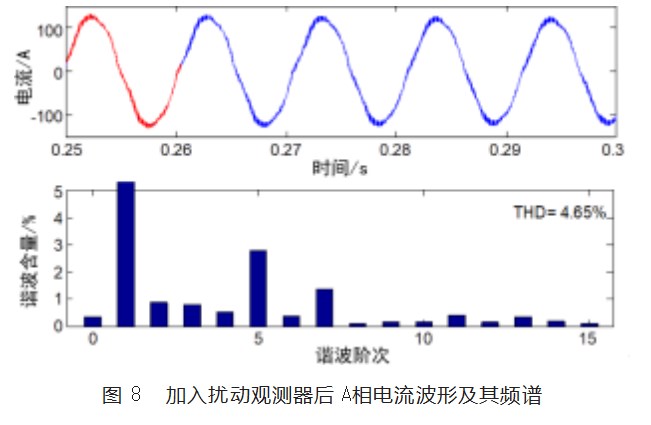
　　从图8可以看出，加入扰动观测器后，比较图7，A相电流波形在过零点和峰值处的畸变有着明显改善，同时正弦度也有了提高。从频谱图可以看出，加入扰动观测器后，A相电流的5次和7次谐波分别为2.74%和1.53%，THD为4.65%。较没加入扰动观测器，THD减小了16%，5次和7次谐波分别减小了26%和17%。这充分说明，本文所提的扰动观测器，可以抑制由于逆变器死区时间引起的相电流5次和7次谐波。同时，也可以实现d-q轴电流的解耦控制。

　　4结束语

　　永磁同步电机d-q轴电流的耦合性、逆变器的非线性和电机参数的时变性，使得相电流通常存在多种干扰，其表征为电流的谐波。本文在以上扰动的基础上，分析了扰动模型和永磁同步电机的实际模型，在此基础上，提出一种扰动观测器。通过扰动观测器观测d-q轴电流的耦合项和扰动项，然后再补偿至d-q轴电流中，并且利用Lyapunov稳定性判定方法对其稳定性进行分析，同时给出了参数选取方法。该方法简洁有效，仿真结果表明，其可以实现d-q轴电流解耦控制，并且有效地抑制了定子电流中的5次和7次谐波分量，使得THD减小了16%，5次和7次谐波分别减小了26%和17%。

　　参考文献：

　　[1]陈哲,张序轩,刘春强,等.基于比例谐振型自抗扰控制的永磁同步电机电流解耦及谐波抑制策略研究[J].中国电机工程学报,2022,42(24):9062-9072.

　　[2]ZHOU S C,LIU K,HU W,et al.Harmonic-Separation-Based Direct Extraction and Compensation of Inverter Nonlinearity for State Observation Control of PMSM[J].IEEE Access,2021(9):142028-142045.

　　[3]周世超,刘侃,丁荣军,等.基于谐波分离的逆变器非线性因素直接提取和补偿方法[J].中国电机工程学报,2021,41(22):7763-7771.

　　[4]ZHANG R F,YIN Z G,Na Du,et al.Robust Adaptive Current Con⁃trol of a 1.2 MW Direct-Drive PMSM for Traction Drives based on Internal Model Control with Disturbance Observer[J].IEEE Transactions on Transportation Electrification,2021(9):1466-1481.

　　[5]赵法强,汪建波,袁汉凯.基于滑模观测器扰动抑制的永磁同步电机模型预测控制方法[J].微电机,2021,54(8):92-97.

　　[6]张志刚,李腾,杜劭琨,等.基于死区补偿的PMSM转矩脉动抑制研究[J].控制工程,2021,28(6):1108-1114.

　　[7]张剑,温旭辉,李文善,等.基于谐波观测器的永磁同步电机谐波电流抑制策略研究[J].中国电机工程学报,2020,40(10):3336-3349.

　　[8]Zhuangyao Tang,Bilal Akin.Suppression of Dead-Time Distor⁃tion Through Revised Repetitive Controller in PMSM Drives[J].IEEE Transactions on Energy Conversion,2017,32(3):918-930.

　　[9]刘兵,周波,倪天恒.基于广义二阶积分器的SPMSM无位置传感器控制逆变器非线性补偿策略[J].中国电机工程学报,2018,38(11):3365-3374.

　　[10]TANG Z Y,Akin B.A New LMS Algorithm Based Dead-time Compensation Method for PMSM FOC Drives[J].IEEE Transac⁃tions on Industry Applications,2018,54(6):6472-6484.

　　[11]韩坤,孙晓,刘秉等.一种永磁同步电机矢量控制SVPWM死区效应在线补偿方法[J].中国电机工程学报,2018,38(2):620-627.

　　[12]袁登科,徐延东,李秀涛.永磁同步电机变频调速系统及其控制[M].北京:机械工业出版社,2015.

　　[13]代攀.永磁同步电机电流环谐波抑制技术研究[D].武汉:华中科技大学,2014.

　　[14]王莉娜,朱鸿悦,杨宗军.永磁同步电动机调速系统PI控制器参数整定方法[J].电工技术学报,2014,29(5):104-117.