摘要：为减少数控加工系统的加工误差，提出了一种基于长短时记忆神经网络(LSTM-NN)的计算机数控机床轨迹跟踪控制参考轨迹修正方法。该方法的实现是通过使用LSTM-NN建立实际轨迹与伺服系统参考轨迹之间的映射，并在不改变控制器的情况下修改参考轨迹以补偿跟踪误差。具体而言，首先分析数控系统伺服系统的结构，并建立单轴数学模型。其次，根据系统模型选择LSTM-NN的输入特征，运用伺服系统的实际轨迹和参考轨迹来训练LSTM-NN。最后生成可根据参考轨迹修改输入的模型。相较于三环PID控制伺服系统与LSTM神经网络逆模型控制系统的轮廓控制，所提出的方法在数控系统运行后的轮廓误差降低了11µm，有效提高了加工精度。

　　关键词：计算机数控(CNC)；LSTM-NN；跟踪控制

　　引言

　　数控加工的主要目的是减少加工误差。一般有两种方法：轮廓控制和轨迹跟踪控制[1-2]。轮廓控制旨在减少加工过程中的轮廓误差，已有学者进行了研究[3-4]。与轮廓控制不同，轨迹跟踪控制旨在提高各轴的跟踪性能，控制器结构简单，鲁棒性好。为获得良好轨迹跟踪控制性能，采用了许多传统控制方法，如滑模控制[5-6]和前馈控制[7-8]。近年来，迭代学习被用于轨迹跟踪控制[9-11]，但其缺点是需要在同一轨迹上重复运行。需要一种能够实现高精度轨迹跟踪控制并适用于不同轨迹的控制算法。随着计算能力的提高，人工神经网络在轨迹跟踪控制中的应用越来越广泛[12-14]。由于其独特的学习能力，神经网络可以在训练过程中学习系统的动力学，并将其应用于控制系统。Wai R J[15]提出了一种滑模神经网络(SMNN)控制系统，用于n刚性连杆机器人的轨迹跟踪控制，以实现高精度的位置控制。Chen S[16]提出了一种将人工神经网络用于迭代学习控制的方法，以减小多轴工业机器人的跟踪误差。使用高保真动态模拟器，针对给定的期望轨迹，对外部命令进行迭代优化，以补偿机器人内环动力学。然后，使用这些期望轨迹和相应的细化输入轨迹训练多层神经网络，以仿真非线性内环动力学的动态逆。最后，Li Q[17]提出了一种基于DNN的算法作为一个附加模块，以提高经典反馈控制器的跟踪性能。给定所需轨迹，DNN根据其学习经验为控制器提供定制的参考输入。

　　实际加工时，封装在机床中的控制器很难修改。因此，修改参考轨迹的方法更为实用。本文提出了一种基于闭环伺服系统LSTM-NN模型的轨迹跟踪方法。首先，分析了伺服系统各部分的动态特性，建立了系统模型。然后，通过分析系统传递函数，选择LSTM-NN的输入特征并对其进行训练，以建立参考轨迹与实际轨迹之间的映射。最后，利用训练好的LSTM-NN，得到修改后的参考轨迹，用于提高系统的跟踪精度。本文的主要贡献体现在本文介绍了一种新的基于LSTM-NN的轨迹跟踪控制方法，该方法在不修改伺服系统控制器的情况下，提高了加工精度，适合于实际应用。

　　1系统模型

　　三轴数控机床系统由3个单轴伺服系统组成。由于3个轴之间耦合性较弱且系统模型相似，本文将对单轴伺服系统进行分析并建模。如图1所示，单轴伺服系统一般分为伺服驱动器、伺服电机和机械传动3部分，接下来分别对这3部分进行建模。

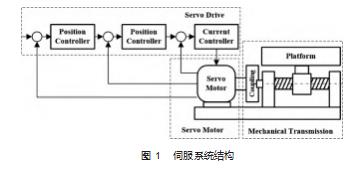
　　1.1机械传动部分

　　机械传动部分的动力学方程为：

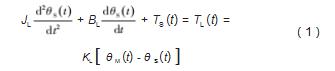
　　式中：JL为总惯性矩；BL为总阻尼因子；KL为总刚度；θS为输出角；θM为期望角；TS为扰动；TL为总扭矩。

　　为便于分析，考虑TS=0，将转动运动转换为直线运动，然后进行拉普拉斯变换，得到机械传动部分的传递函数：

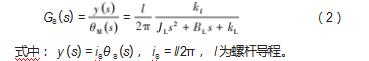
　　1.2伺服电机

　　伺服电机通常是永磁同步电机。在d-q坐标系下，用以下4个方程来建立永磁同步电机的数学模型。

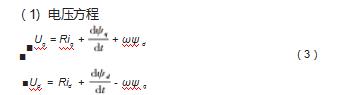
　　式中：Ud和Uq分别为d轴和q轴的电压；R为定子电阻；ψd和ψq分别为d轴和q轴的磁通；id和iq分别为d轴和q轴的电流；ω为转子角速度。

　　1.3伺服驱动器

　　在伺服系统中，通常采用三回路控制器，电流和速度环采用比例积分(PI)控制器，位置环采用P控制器。伺服驱动器包括逆变器、低通滤波器、电流环控制器、速度环控制器和位置环控制器，下面分别对其进行建模。

　　2控制策略和LSTM-NN结构

　　2.1控制策略

　　基于ANN逆模型的传统控制框架如图3所示。采用神经网络逆模型作为前馈控制器，通过修改控制输入补偿系统的跟踪误差，并采用反馈控制器抑制未知扰动和参数不确定性。在此控制框架中，建立了开环被控对象的逆模型，该模型由于不可避免的系统不确定性而限制了模型的精度。

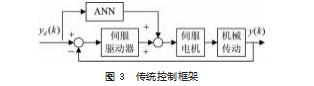
　　本文提出的闭环LSTM轨迹跟踪控制框架如图4所示。在闭环LSTM中，控制系统可分为两部分。第一部分是一个单轴伺服系统，其中包括一个采用三环控制的伺服驱动器，一个伺服电机和机械传动部分。闭环PEA的输入为参考轨迹yr(k)，输出为实际轨迹y(k)。第二部分是基于LSTM-NN的轨迹修正模块。其输入为给定轨迹yd(k)，输出为修改后的参考轨迹yr(k)。伺服系统中的三环伺服驱动器既能保证系统的稳定性，又能实现一定的轨迹跟踪精度。对于相同的参考轨迹，闭环系统可以产生类似的跟踪误差，即与开环系统相比，该系统具有更好的鲁棒性和可重复性。对于这样的闭环系统，可以使用具有强大时间序列逼近能力的LSTM-NN学习yd(k)与yr(k)之间的映射关系。利用训练好的LSTM-NN对参考轨迹进行修正，提高了整个伺服系统的跟踪性能。

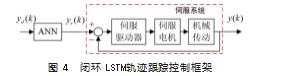
　　提出的Closed-LSTM如图5所示，包括一个训练阶段和一个测试阶段，使用LSTM-NN学习yd(k)和yr(k)之间的映射。在训练阶段，把y(k)看作yd(k)，实际轨迹y(k),y(k+1),⋯,y(k+N)作为LSTM-NN的训练输入，参考轨迹yr(k),yr(k+1),⋯,yr(k+N)作为LSTM-NN的训练输出。在测试阶段，利用训练好的LSTM-NN对期望轨迹进行修正，得到新的参考轨迹。LSTM-NN的输入为期望轨迹yd(k)，输出为参考轨迹yr(k)。当伺服系统中输入参考轨迹yr(k)时，如果LSTM-NN绝对准确，则其实际轨迹y(k)等于期望轨迹yd(k)。

　　2.2特征选取

　　基于单轴伺服系统的简化模型(8)，将传递函数转化为离散形式：

　　式中：y(k)和yr(k)分别代表单轴伺服系统的在k时刻的实际轨迹和参考轨迹。

　　基于离散时间表达式，k时刻的参考轨迹和实际轨迹y(k+j),j=-1,0,⋯,5与参考轨迹yr(k-1)相关。同时，由于速度信号可以表示为位置信号的差分，并且为了提高输入特征的丰富度，本文选择y(k+j),j=-1,0,⋯,5和y.(k+j),j=-1,0,⋯,5作为输入特征，yr(k)作为输出特征，即当前时刻的参考轨迹由前一时刻、当前时刻和后5个时刻的实际轨迹和实际速度计算而来。而参考位移yr(k-1)作为隐藏信息被LSTMNN的长期和短期记忆特征所保留和拟合。

　　2.3训练数据

　　利用LSTM-NN建立实际轨迹与参考轨迹之间的映射关系，训练LSTM-NN的数据需要覆盖大部分特征空间，充分激发系统的响应特性。在这个意义上，幅值逐渐增大的正弦轨迹能够覆盖机床运行轨迹能够经历的所有特征空间，非常适合作为本文的训练集，其表达式如下：

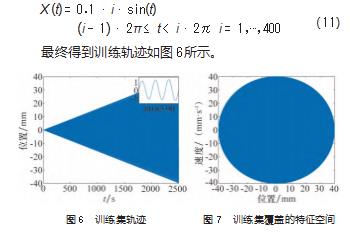
　　训练集的特征分布图如图7所示，能够覆盖所有机床运行轨迹能够到达的特征空间，具有很好的泛化性能。

　　2.4 LSTM-NN模型

　　2.4.1 LSTM-NN结构

　　LSTM神经网络是一种对序列响应进行模型拟合的神经网络。LSTM作为一种特殊的RNN，通过在标准RNN中加入长时记忆序列，可以适应长时记忆和短期记忆。在时域，LSTM-NN将返回两个信息：cell状态和hidden状态。LSTM-NN具有良好的记忆能力，适用于长期依赖问题。

　　调整神经网络参数后，确定神经网络结构如图8所示，其中包含3个隐藏层64个神经元，dropout参数为0.2。求解器为Adam，预设的max-epoch为10 000，min-batchsize为128，学习率初始化为0.01。

　　2.4.2 LSTM-NN训练

　　LSTM-NN的权值参数需要离线训练。简而言之，训练过程就是通过BP算法迭代更新权值参数，找到最优权值矩阵。

　　LSTM-NN的训练输入为实际的轨迹信息(滤波后的位置和速度)，网络训练输出为估计的参考轨迹r(t)。损失函数定义为估计参考轨迹r(t)与实际参考轨迹y(t)之间的均方根误差(root mean square error，RMSE)，t时刻的表达式为：

　　3实验结果

　　3.1实验平台介绍

　　本文采用了三轴数控机床实验平台，主要由1个机械本体、3个GTHD伺服驱动器、实时仿真控制器及计算机组成，系统的整体效果如图9所示。

　　该实验平台的工作原理为：首先在计算机上的SIMULINK中实现控制算法，然后SIMULINK将相应的代码和模块编译成嵌入式系统可运行的目标文件，将目标文件下载到实时仿真控制器中。实时仿真控制器通过GTHD伺服驱动器与被控伺服电机连接，伺服电机带动3个轴进行运动。其中，伺服驱动器工作在模拟速度模式，也就是电流环和速度环在伺服驱动器端，位置环在实时仿真控制器端。伺服驱动器为GTHD-006AAP1-00伺服驱动器，平台使用的电机为多摩川TS4607N2190E200伺服电机，实时仿真控制器为dSPACE公司的产品，型号为DS1103 PPC Controller Board。

　　3.2结果对比

　　在工业生产中，常用于机床伺服电机的控制算法是三环控制。为了验证本算法的有效性，本实验以常用的皇冠轨迹作为测试轨迹，如图10所示。比较了两种控制系统运行后的轮廓误差：(1)三环PID控制伺服系统；(2)经过训练后的LSTM神经网络逆模型控制系统。

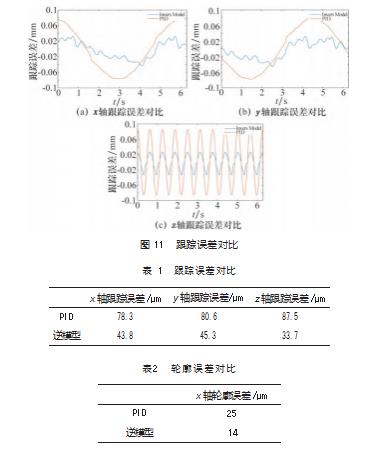
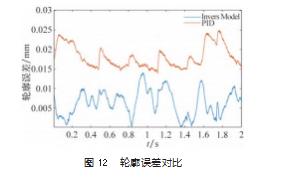
　　对于两种控制算法，给定轨迹均为皇冠曲线，对于算法1，伺服系统的输入轨迹为皇冠曲线；对于算法2，给定轨迹为皇冠曲线，参考轨迹为给定轨迹经过LSTM-NN修改后的轨迹，伺服系统的输入轨迹为参考轨迹。如图11和表1所示，经过逆模型补偿后3个轴的单轴跟踪误差均有很大的下降。如图12和表2所示，轮廓误差也有很大的下降，最大轮廓误差为25µm，降低了11µm。

　　4结束语

　　针对数控机床在加工时，控制器难以修改导致加工精度提高困难问题，本文提出了一种基于闭环伺服系统LSTM-NN模型的轨迹跟踪控制方法，该方法通过建立实际轨迹与参考轨迹之间的映射关系，对参考轨迹进行修正和补偿，提高了单轴轨迹跟踪能力，从而降低了机床加工过程中的轮廓误差。实验结果表明经过逆模型补偿后3个轴的单轴跟踪误差均有很大的下降，轮廓误差也有很大的下降。与现有的轮廓控制方法相比，所提出的控制方法不修改机床本身控制器的情况下，降低了11µm轮廓误差，有效地提高了数控加工的精度。在后续的研究工作中将对数控机床轨迹跟踪控制中的抗扰问题开展进一步研究。

　　参考文献：

　　[1]Ramesh R,Mannan M A,Poo A N.Tracking and contour error control in CNC servo systems[J].International Journal of Ma⁃chine Tools and Manufacture,2005,45(3):301-326.

　　[2]Zhou D,Gui J,Yang J,et al.Sliding mode control with extended state observer for multi-axis motion control system[C]//2019 Chi⁃nese Control Conference(CCC).IEEE,2019:3196-3201.

　　[3]Chen S L,Chou C Y.Contouring control of multi-axis motion sys⁃tems for NURBS paths[J].IEEE Transactions on Automation Sci⁃ence and Engineering,2015,13(2):1062-1071.

　　[4]Li J,Qi C,Li Y,et al.Prediction and compensation of contour er⁃ror of CNC systems based on LSTM neural-network[J].IEEE/ASME Transactions on Mechatronics,2021,27(1):572-581.

　　[5]Xu Q.Precision motion control of piezoelectric nanopositioning stage with chattering-free adaptive sliding mode control[J].IEEE Transactions on Automation Science and Engineering,2016,14(1):238-248.

　　[6]Xu Q.Continuous integral terminal third-order sliding mode mo⁃tion control for piezoelectric nanopositioning system[J].IEEE/ASME Transactions on Mechatronics,2017,22(4):1828-1838.

　　[7]Jian Y,Huang D,Liu J,et al.High-precision tracking of piezo⁃electric actuator using iterative learning control and direct in⁃verse compensation of hysteresis[J].IEEE Tran-sactions on In⁃dustrial Electronics,2018,66(1):368-377.

　　[8]Gibbs A J.The design of digital filters[J].Australian Telecommu⁃nication Research Journal,1970(4):29-34.

　　[9]Tomizuka M.Zero phase error tracking algorithm for digital con⁃trol[J].1987,109(1):65-68.

　　[10]Kormylo J,Jain V.Two-pass recursive digital filter with zero phase shift[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1974,22(5):384-387.

　　[11]褚金奎,李晋,李金山,等.基于改进A*算法的POL-Robot路径规划[J].机电工程技术,2022,51(8):1-5.

　　[12]Li J,Huang Y,Li Q,et al.Closed-LSTM neural network based reference modification for trajectory tracking of piezoelectric ac⁃tuator[J].Neurocomputing,2022,467:379-391.

　　[13]Wang F,Liu Z,Chen C L P,et al.Adaptive neural network-based visual servoing control for manipulator with unknown out⁃put nonlinearities[J].Information Sciences,2018,451:16-33.

　　[14]绳红强,黄海英,崔毅刚.基于A*蚁群融合算法的避障路径规划研究[J].机电工程技术,2022,51(7):45-49.

　　[15]Wai R J.Tracking control based on neural network strategy for robot manipulator[J].Neurocomputing,2003(51):425-445.

　　[16]Chen S,Wen J T.Industrial robot trajectory tracking control us⁃ing multi-layer neural networks trained by iterative learning control[J].Robotics,2021,10(1):1-20.

　　[17]Li Q,Qian J,Zhu Z,et al.Deep neural networks for improved,impromptu trajectory tracking of quadrotors[C]//2017 IEEE In⁃ternational Conference on Robotics and Automation(ICRA).IEEE,2017:5183-5189.