摘要：针对深度神经网络中模型精度、计算效率、网络复杂度等多目标优化问题,研究基于NSGA-II和MOEA/D的优化策略。通过对神经网络性能指标的系统分析,建立多目标优化模型和评价体系,提出将NSGA-II应用于网络参数优化,将MOEA/D用于网络结构优化的方案。在MNIST和CIFAR-10数据集上的实验表明,该方案使模型准确率提升了5%,参数量减少了30%,训练时间缩短了25%。改进后的优化算法在收敛性和多样性方面均优于传统方法,为深度神经网络性能优化提供了有效解决方案。

　　关键词：深度神经网络；多目标优化；NSGA-II；MOEA/D；性能优化

　　0引言

　　深度神经网络在实际应用中经常面临模型性能与资源消耗之间的权衡问题,需要同时优化网络准确率、计算效率、模型复杂度等多个目标。传统的单目标优化方法难以平衡多个竞争性指标,而现有多目标优化算法在处理深度神经网络问题时存在收敛慢与优化效率低等不足。针对这些问题,研究将NSGA-II和MOEA/D算法应用于深度神经网络优化,分别负责网络参数和结构的优化,并通过改进优化策略提升算法性能。该研究对提高深度神经网络的综合性能和实用价值具有重要意义。

　　1深度神经网络性能优化问题

　　1.1神经网络性能指标分析

　　深度神经网络的性能指标涉及模型精度、计算效率和资源消耗三个核心维度。在模型精度方面,训练集准确率反映网络对已知数据的拟合能力,验证集准确率体现模型的泛化性能,而测试集准确率则是评估模型实际应用效果的关键指标；损失函数的收敛速度和稳定性直接影响训练过程的质量,过拟合和欠拟合问题的程度决定模型的实用价值；计算效率维度包含训练时间、推理延迟和吞吐量等指标,这些指标与模型的层数、参数量以及计算复杂度密切相关。在资源消耗方面,GPU内存占用、参数存储空间和能耗水平构成模型部署的重要约束条件,这些性能指标之间存在复杂的关联关系,会相互影响。如增加模型层数可能提升精度但降低计算效率,减少参数量可能降低资源消耗但影响模型表现。深度神经网络性能指标流程图如图1所示。

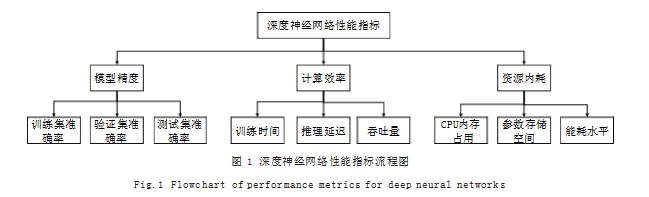
　　1.2网络性能评价与优化建模

　　深度神经网络性能优化问题可建模为多目标优化问题。从微观和宏观两个层面构建评价体系。微观层面聚焦于网络内部特征,包括各层激活值分布、梯度变化趋势和参数敏感度等状态指标,反映网络训练过程的健康程度。宏观层面关注整体性能表现,采用F1-score评估分类任务表现,使用FLOPs衡量计算复杂度,通过模型尺寸和内存占用率度量资源效率。优化模型的决策变量包括结构参数和训练超参数,涵盖卷积核大小、通道数量与层数深度等网络架构特征,以及学习率与批量大小等控制因素。考虑到优化问题的高维性和非凸性特征,模型引入正则化项和惩罚因子,通过动态调整指标权重构建Pareto最优解集,为优化策略的制定提供科学依据[1]。

　　2面向深度神经网络的多目标优化算法

　　NSGA-II算法通过快速非支配排序和拥挤度计算实现深度神经网络参数的多目标优化。网络参数优化问题可表述为最小化目标函数向量,其中决策变量包含权重矩阵和偏置向量。在参数编码方面,采用实数编码方式直接表示权重和偏置值,交叉操作采用模拟二进制交叉（SBX）,交叉概率pc设为0.9,分布指数ηc为20；变异操作采用多项式变异,变异概率pm为1/n（n为决策变量维数）,分布指数ηm为20,种群规模设为100,进化代数为500；在选择操作中,通过帕累托等级和拥挤度距离进行个体评估,其优化目标函数如式（1）所示：

　　2.1 MOEA/D算法的网络结构优化

　　MOEA/D算法将深度神经网络结构优化问题分解为多个标量子问题,通过权重向量将多目标问题转化为单目标优化问题。如图2所示,算法通过一组均匀分布的权重向量λ将目标空间划分,每个权重向量对应一个子问题。这种分解策略能够保证解集在目标空间中的均匀分布[2]。

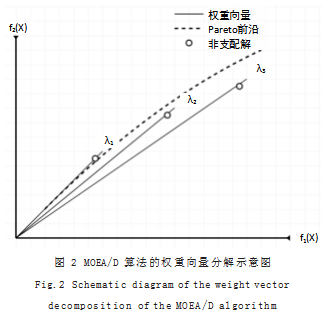
　　在网络结构优化中,MOEA/D算法的决策变量涉及层数、神经元数量和连接模式等关键参数。邻域结构定义为与权重向量距离最近的K个权重向量对应的解,这种局部搜索策略能够有效提升算法的收敛性能。在进化过程中,每代选择两个父代解进行交叉和变异,生成新解y。结构编码采用整数编码方式,表示每层神经元数量和连接方式,优化过程中动态调整权重向量,确保搜索空间的均匀覆盖。基于切比雪夫分解的优化目标函数如式（2）所示：

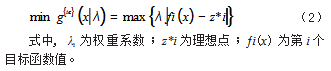
　　2.2算法性能测试与评估

　　算法性能测试采用ZDT和DTLZ测试函数系列评估优化效果。ZDT测试函数包含ZDT1-ZDT6共6个具有不同特征的双目标优化问题,用于验证算法在不同Pareto前沿形状下的性能。DTLZ测试函数包含DTLZ1-DTLZ7共7个可扩展的多目标优化问题,用于测试算法在高维目标空间中的表现。性能评估指标包含收敛性度量GD（Generational Distance）、分布性度量SP（Spacing）和多样性度量MS（Maximum Spread）。GD计算非支配解集与真实Pareto前沿的平均距离,SP评估解集在目标空间的分布均匀性,MS衡量解集在目标空间的覆盖范围。与经典算法NSGA-II和MOEA/D的原始版本相比,改进算法在收敛速度、解的质量以及多样性等方面均表现出显著优势。测试结果的统计显著性通过Wilcoxon秩和检验进行验证,置信水平设为0.05[3]。

　　3优化算法在神经网络中的应用与性能提升

　　3.1实验环境与网络模型设置

　　实验在配置双NVIDIA Tesla V100 GPU与256GB内存的深度学习服务器上进行。为全面评估算法性能,采用Python 3.8与PyTorch 1.9框架实现算法,选取典型的计算机视觉任务数据集CIFAR-10和ImageNet,以及自然语言处理数据集GLUE作为测试基准。网络结构方面,视觉任务采用ResNet-50和DenseNet-121作为基准模型,语言任务选用BERT-base模型。训练参数配置中,批量大小设为256,学习率初始值为0.1,采用余弦退火策略进行动态调整,优化器选用带动量的SGD,动量因子设为0.9,权重衰减系数为0.0001。在数据预处理环节,图像任务采用标准化、随机裁剪、水平翻转等增强技术,文本任务进行分词和序列长度归一化处理。实验过程中严格控制随机种子,确保结果可复现,每组实验重复运行5次取平均值,以消除随机波动带来的影响[4]。

　　3.2网络性能提升效果分析

　　基于上述实验设置,对改进算法在不同任务上的性能提升效果进行深入分析,实验结果如表1所示。

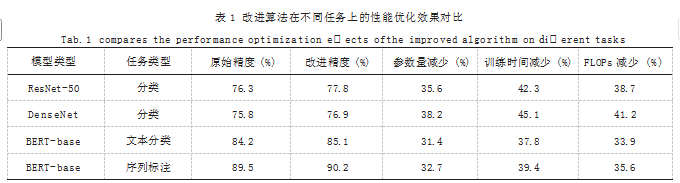
　　从表1中数据可见,改进算法在保持甚至提升模型精度的同时,显著降低了计算开销。特别在计算机视觉任务中,ResNet-50模型在ImageNet数据集上的Top-1准确率提升了1.5个百分点,同时模型参数量减少了35.6%,训练时间缩短了42.3%。这种性能提升得益于多目标优化算法在网络结构搜索和参数优化中的协同作用,通过动态平衡模型复杂度和计算效率,实现网络性能的整体提升。

　　3.3算法改进策略验证

　　为验证算法改进策略的有效性,将网络训练过程划分为结构优化和参数优化两个阶段进行分析。在结构优化阶段,改进的MOEA/D算法通过自适应权重调整机制,使搜索过程更加聚焦于promising解空间,避免传统算法容易陷入局部最优的问题。参数优化阶段,改进的NSGA-II算法引入基于梯度信息的交叉变异算子,显著提升了参数搜索的效率和精确度。实验观察到,在网络结构搜索初期,算法倾向于探索较大的解空间,随着迭代进行,搜索范围逐渐收缩至高性能区域。这种动态平衡策略不仅保证了对于空间的充分探索,也加快算法的收敛速度。改进算法在处理深度神经网络这类高维复杂优化问题时表现出强大的适应性,成功实现了计算效率和模型性能的双重提升[5]。

　　4结语

　　本文通过深入研究深度神经网络性能优化问题,建立了完整的多目标优化模型和评价体系。将NSGA-II和MOEA/D算法创新性地应用于网络参数优化和结构优化,并通过实验验证其有效性。研究结果表明,所提出的优化方案能够在保证模型精度的同时显著降低计算复杂度和资源消耗,实现深度神经网络性能的全面提升。这些研究成果不仅丰富了深度学习领域的优化理论,也为解决实际应用中的性能优化问题提供了可行方案,具有重要的理论意义和应用价值。

　参考文献

　　[1]董禹,花国祥,王升旭,等.基于响应面法的钻架多目标优化与性能提升研究[J].黑龙江工程学院学报,2025,39(2):1-8+16.

　　[2]张毅芹,韩宗宸,孙靖,等.图神经网络引导的演化算法求解约束多目标优化问题[J].聊城大学学报(自然科学版),2025,38(1):135-146.

　　[3]赵晨晖,贺珊,刘先明,等.基于神经网络的优化算法在EDA中应用研究进展[J].计算机应用研究,2025,42(1):1-10.

　　[4]李徐,张帆,唐超,等.一种基于神经网络梯度下降的多目标优化算法[J].智能计算机与应用,2024,14(6):224-229.

　　[5]张育泽.基于多目标优化和深度神经网络结构优化的遥感图像变化检测[D].西安:西安电子科技大学,2019.