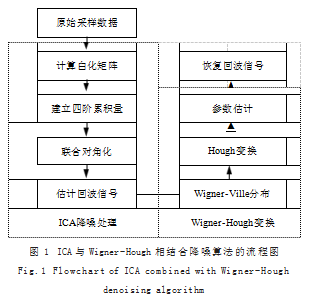
摘要：针对近距离合成孔径微波成像过程中背景噪声干扰问题,本文提出了一种基于脉冲线性调频体制信号的噪声抑制算法。该算法将独立分量分析（ICA）与Wigner-Hough变换相结合,无需提前测量背景噪声,且具有噪声抑制效果好、工程易于实现的优点。在半实物仿真系统中,利用标准目标进行测试,该算法将回波信号的信噪比提高了10dB左右,通过标准目标的成像结果,验证了该噪声抑制算法的有效性和可行性。

　　关键词：独立分量分析；Wigner-Hough变换；脉冲线性调频；逆散射成像

　　0引言

　　独立分量分析（ICA）基于高阶统计量的特征提取方法,能够有效获取相互独立的信源量化特征,ICA被认为是PCA的高阶扩展[1],仅从观测数据的统计信息出发,实现传输信道的辨识及信源的估计。Herault和Jutten等人最早提出了一种基于反馈神经网络的ICA方法,实现了两个独立信源的分离[2]。Cardoso着重研究了高阶累积量的ICA方法,并最终形成易于实现的特征矩阵联合近似对角化（JADE）算法[3]。Cmon系统地阐述和研究了ICA问题,并提出了ICA概念以及基于最小互信息的目标函数[4]。在此基础上,许多学者提出了不同的算法,Bell和Sejnowski通过研究最优非线性函数与信源概率密度函数的关系,提出了一种基于前向网络结构和信息传输最大化的Infomax算法[5]。Kiyotoshi和Matsuoka提出了一种分离非平稳信号的算法[6],从而把ICA问题的研究工作向实际应用推进了一大步。Oja提出了一种固定点迭代的FASTICA算法[7],该算法具有工程上易于实现、计算效率极高等特点,解决了众多实际问题。时频分析方法着眼于非平稳信号的时间和频率特征,将一维的信号扩展到二维的时间和频率参数平面上进行观察,从而获得信号频率随时间的变化特征。Gabor最早提出了利用时间和频率两个变量联合对信号进行描述,为时间和频率联合域内的信号分析奠定了基础[8]。在此之后,Avargel和Cohen等人提出了短时傅里叶变换[9],该变换是一种利用窗函数在信号的时间轴上滑动的分析方法。Wigner在量子力学中提出了著名的Wigner分布[10],后来由Ville将其引入信号处理领域,从而形成了完整意义上的双线性时频分析方法的基础,即Wigner-Ville分布。Hough从图形特征分析的角度出发,提出了Hough变换,研究人员将其应用到Wigner-Ville分布的时频平面,形成了Wigner-Hough变换[11],Wigner-Hough变换已经成为信号处理、遥感遥测等许多领域使用的重要工具。

　　4三维成像系统的半实物仿真

　　本文搭建了三维成像系统的微波暗室半实物仿真平台,如图2所示。工作参数如下：频率范围20GHz~26GHz,沿着频率方向的采样点数为128；沿着Z轴方向采样距离设置为1m,采样间隔5mm；角度方向扫描范围360°,角度方向的采样点数设置为1024。半实物仿真系统采用安捷伦公司的矢量网络分析仪E8363C,产生20GHz~26GHz线性调频信号,为了提高回波信噪比,设置中频带宽为1kHz。收发天线采用DRG公司的SAS-574角锥喇叭,该角锥喇叭的工作频率范围为18GHz~40GHz,能够满足成像系统使用的需求,水平和垂直方向的波束宽度为50°,而且具有较低的旁瓣。为了保证回波信号的质量,空间中的每一位置采样时间为2s,采集所有数据的时间大约为73小时。

　　为了验证成像系统的成像质量以及系统分辨率,设计了标准目标如图2所示。标准目标采用了木质结构作为支撑体,分别将测试分辨率和清晰度的金属条贴于结构体两侧,吸波材料贴在结构体的非目标区域,减小构体两侧目标彼此之间的干扰以及目标和周围环境彼此之间的干扰。用宽度为1 cm的铝箔设计数字“1”“2”“3”“4”来验证系统成像的清晰度。使用图2（b）中的金属线条来验证系统沿着X方向的分辨率,垂直排列的线条宽度为1cm,长度为10cm,间距分别为3mm、4mm、5mm、6mm,结构体弧度较小,Y方向的分量忽略不计。使用图2（c）中的金属线条来验证沿着X、Z两个方向的联合分辨率,金属线条的长宽不变,只是排列方式变为与X轴成±45°的排列,间距分别是5mm、7mm、9mm、11mm。

　　首先,利用ICA处理方法对原始采样数据沿着频率方向进行噪声抑制,提高回波数据信噪比。利用特征矩阵的联合近似法分离噪声信号和回波信号,噪声分离前后采样数据的一维距离像如图3(a)所示。对Wigner-Ville分布变换后的数据进行Hough变换,其结果如图3(b)和3(c)所示,对ICA降噪处理后的回波数据进行Wigner-Hough变换后,目标的信噪比30dB左右,而对未进行降噪处理的回波数据进行Wigner-Hough变换后,目标的信噪比20dB左右,此时估计精度提高10dB。

　　在参数估计平面,寻找回波信号峰值对应的坐标位置,提取出回波信号的参数,完成信号的估计,利用恢复后的回波数据进行目标三维空间重构,其投影后的结果如图4所示。

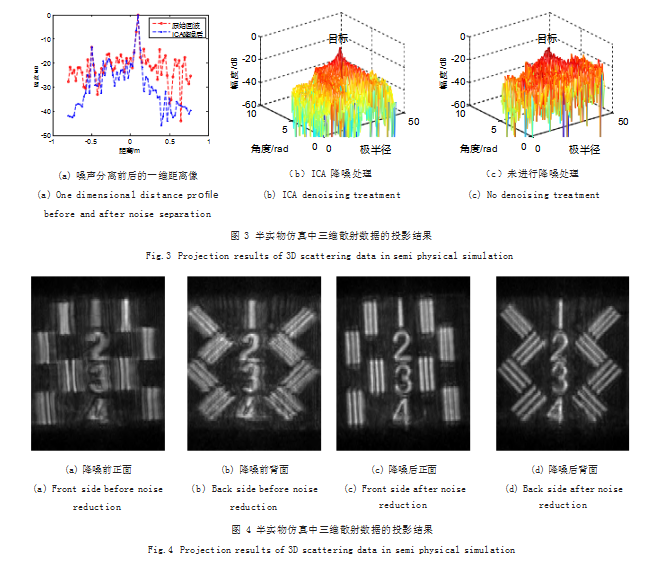
　　与降噪前的成像比较,降噪后的成像结果中的背景噪声明显被抑制,整体的清晰度增加了,结构体两侧的标准目标“1”“2”“3”“4”的轮廓更加清晰,尤其是数字“4”周围存在的干扰被有效抑制。在图4（c）中,当三根金属条间距为5mm时,金属条之间的间隙明显更加清晰,此时,可以认为沿着X方向的分辨率优于5mm,在图4（d）中,当三根金属条间距为7mm时,金属条之间的间隙清晰度差不多,可以认为沿着X、Z两个方向的联合分辨率大约为7mm。

　　5结语

　　基于近距离合成孔径微波成像中宽带脉冲线性调频信号回波特点,本文提出了一种ICA方法与Wigner-Hough变换相结合的噪声抑制算法。该算法利用ICA处理方法完成有用信号和噪声信号的分离,提高了输入回波信号的信噪比,利用Wigner-Hough变换完成差频回波信号的参数估计,提高了参数估计的总精度。该算法采用了四阶统计量的特征矩阵的联合近似对角化（JADE）法,工程上易于实现。分别通过理论模型和半实物仿真系统验证了该噪声抑制算法的有效性和可行性。

　参考文献

　　[1]ALMEIDA L B.ICA of Linear and Nonlinear Mixtures Based on Mutual Information[J].International Joint Conference on Neural Networks,2001(4):2991-2996.

　　[2]JUTTEN C,HERAULT A.Blind Separation of Sources,Part I:An Adaptive Algorithm Based on Neuromimetic Architecture[J].Signal Processing,1991,24(1):1-10.

　　[3]CARDOSO J F,SOULOUMIAC A.Blind Beamforming　for Non-Gaussian Signal[J].IEE Proceedings on Radar and Signal Processing,1993,40(6):362-370.

　　[4]COMON P.Independent Component Analysis,A New Concept?[J].Signal Processing,1994,36:287-314.

　　[5]BELL A J,SEJNOWSKI T J.An Information-maximization Approach to Blind Separation and Blind Deconvolution[J].Neural Computation,1995(7):1129-1159.

　　[6]OHATA M,MATSUOKA K.Frequency-domain Implementation of a Time-domain Blind Separation Algorithm for Convolutive Mixtures of Sources[C]//International Conference on Independent Component Analysis and Signal Separation,2007,4666:528-535.

　　[7]HYVÄRINEN A,OJA E.A Fast Fixed-point Algorithm for Independent Component Analysis[J].Neural Comput ation,1997,9(7):1483-1492.

　　[8]GABOR D.A New Microscope Principle[J].Nature,1948:161-777.

　　[9]AVARGELY,COHEN I.Representation and Identification of Nonlinear Systems in the Short-Time Fourier Transform Domain[J].Springer Topics in Signal Processing,1970,58(1):49-87.

　　[10]WIGNER E P.On the Quatum Correction for Ther modynamic Equilibrium[J].Physical Review,1931,40(40):749-759.

　　[11]BARBARROSSA S.Analysis of Multi Components LFM Signals by a Combined Wigner-Hough Transform[J].IEEE Transactions on Signal Processing,1995,43(6):1511-1515.