摘要：在全球能源危机背景下，新能源汽车与储能行业的迅猛发展对锂离子电池的需求急剧增加，而准确获取电池SOC对于保障电池安全、延长使用寿命及优化系统性能至关重要。针对现有方法存在的精度不足问题，创新性地提出了BiLSTM与KAN相结合的SOC估计模型。在BiLSTM模型框架下捕捉电池状态序列中的双向依赖关系，并将KAN网络引入，使得网络权重不再局限于固定参数，而是被可学习的单变量函数所取代，通过两者的结合有效提升了模型对电池复杂动态特性的学习能力。通过对比实验将BiLSTM-KANs模型与其他主流SOC估计模型进行对比分析，结果显示该模型在估计精度提高了31.7%，表现出了较高的准确性和鲁棒性。提出的BiLSTM-KANs模型为锂离子电池SOC估计研究方向，提供了一种新的思路和方法，具有较高的实际应用价值。

　　关键词：锂电池；SOC估计；双向LSTM；KAN网络；MLP；LSTM；可学习激活函数；预测模型

　　0引言

　　在全球能源危机日益凸显的背景下，近两年新能源汽车与储能行业蓬勃发展，极大地推动了锂离子电池需求的急速增长。然而，锂离子电池作为关键组件，存在电量自然衰减、电荷状态（SOC）直接测量获取困难等问题。因此如何精准估算锂离子电池的电荷状态（SOC）是目前主要的研究方向，当前，锂离子电池电荷状态估计方法主要分为：传统估计法、状态观测法以及数据驱动法[1]。其中数据驱动法是目前国内外学者研究的主流方向，朱月凡等[2]提出基于BiLSTM模型来估算SOC，但该方法存在模型估算精度不高，数据处理繁琐；王志等[3]采用改进LSTM算法，虽然能提高精度，但需要在数据处理上花费大量资源；何复兴等[4]采用GRU模型，结合提出EMD方法对电流进行分解，增大了模型复杂度，但实际精度提升不大；Liu等[5]提出段长短期记忆（SL⁃STM）估计，增强SOC与非线性变化参数之间的数据联动，但分段式也导致SOC估计复杂化。

　　针对上述问题，本文提出了一种BiLSTM（Bi-direc⁃tional Long Short-Term Memory）与KAN（Kolmogorov-Ar⁃nold Networks）相结合的锂电池SOC估计方法，无需过多的初始数据处理，取消之前的固定激活函数，而是被可学习的单变量函数所取代，有效提升了模型对电池复杂动态特性的学习能力，来提升估算精度。并通过一系列对比实验与其他模型进行分析来评估BiLSTM-KANs预测模型[6]在锂电池SOC估计上的性能表现。

　　1基本理论

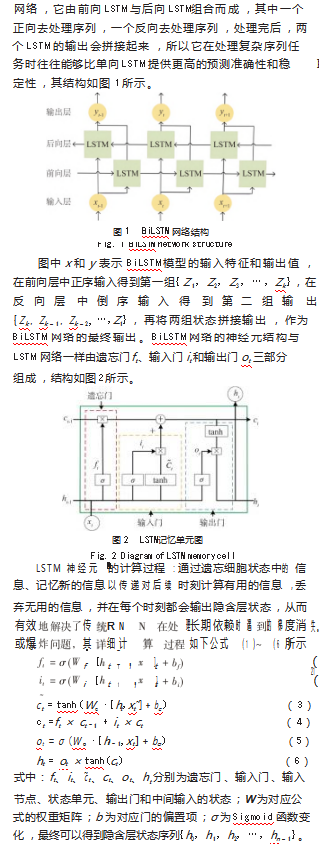
　　1.1双向长短期记忆网络模型（BiLSTM）

       BiLSTM神经网络[7]是在LSTM的基础上延伸而来的

　　4结束语

　　本文利用最新提出的KAN网络与BiLSTM神经网络结合，构建了一个BiLSTM-KANs锂离子电池SOC估计预测模型，该模型结合了BiLSTM和KANs的优势，在处理时间序列数据和复杂关系建模时具有更强的能力。它能够同时捕捉前向和后向的上下文信息，并利用可学习的激活函数来学习和表示数据中的复杂关系。

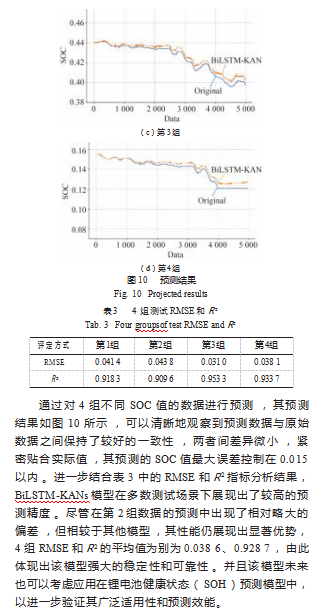
　　从实验结果上也表明了BiLSTM-KANs模型在锂离子电池SOC估计上是优于其他对比模型，尤其是在对比传统模型上。因此本文提出引入KAN网络将激活函数放置在网络的权重上，即权重参数被替换为可学习的单变量函数，可学习的激活函数增强了网络的表达能力和灵活性，有助于提升模型的准确性和可解释性。然而，所提模型依然存在诸多不足，如模型训练上KAN网络的权重参数被替换为可学习的单变量函数，训练时间会延长，模型优化等。综上所述，本文所提BiLSTM-KANs模型为锂离子电池SOC估计研究方向提供了一定的参考价值，并且该模型也可以尝试在锂电池健康状态（SOH）预测上。

　参考文献：

　　[1]米文杰.新能源汽车动力电池SOC估算及优化管理[J].汽车测试报告,2024(7):61-63.

　　[2]朱月凡.基于双向长短时记忆网络的电池荷电状态估计研究[D].南京:南京邮电大学,2023.

　　[3]王志.基于长短期记忆网络的锂电池SOC与SOP的联合估算[D].绵阳:西南科技大学,2023.

　　[4]何复兴.基于数据驱动的锂离子电池荷电状态及健康状态估计研究[D].西安:西安理工大学,2021.

　　[5]Liu D,Wang S,Fan Y,et al.An optimized multi-segment long short-term memory network strategy for power lithium-ion bat⁃tery state of charge estimation adaptive wide temperatures[J].Energy,2024,304:32048-132048.

　　[6]刘娟,雷辉,吕金,等.基于CNN-LSTM的锂离子SOC估计[J].电气传动,2024,54(2):26-31.

　　LIU J,LEI H,LÜJ,et al.SOC estimation of lithium-ion batteries based on CNN-LSTM[J].Electric Drive,2024,54(2):26-31.

　　[7]刘明浩,韩晓明,何晨.基于迁移学习训练的BiLSTM锂电池剩余使用寿命预测[J].控制工程,1-9.

　　LIU M H,HAN X M,HE C.Prediction of remaining service life of bilstm lithium battery based on transfer learning training[J].Control Engineering of China,1-9.

　　[8]张超.基于数据驱动的锂离子电池状态估计[D].太原:山西大学,2023.

　　[9]BOGDANOV I R,BOGDANOV R M.Thermal Parameters of Jet Flows in the Weakly Dissipative Kolmogorov-Arnold-Moser Theory[J].Doklady.Physics,2008,53(12):616-618.

　　[10]G V G,H Y,G V,et al.Detecting somatic mutations in genomic sequences by means of Kolmogorov-Arnold analysis.[J].Royal Society open science,2015,2(8):150143.

　　[11]Knauf A.H.Scott Dumas:"The KAM Story:A Friendly Intro⁃duction to the Content,History,and Significance of Classical Kolmogorov-Arnold-Moser Theory":World Scientific,2014,361 pp.[J].Jahresbericht der Deutschen Mathematiker-Vereini⁃gung,2016,118(2):131-134.

　　[12]Montanelli H,Yang H.Error bounds for deep ReLU networks using the Kolmogorov-Arnold superposition theorem[J].CoRR,2019.

　　[13]Akashi S.The existence of polynomials which are unrepresent⁃able in Kolmogorov-Arnold superposition representation[J].Re⁃sults in Nonlinear Analysis,2018(2):58-64.

　　[14]丁伟健,卢敏,杨忠明,等.基于LSTM与深度矩阵分解的推荐融合模型[J].软件导刊,2024,23(9):41-47.

　　[15]丁伟,邹复民,刘吉顺,等.基于CNN-BiLSTM-Attention的电动装载机电池荷电状态预测[J].电源学报,1-12.

　　[16]蒋泽宇,赵宇波,赵景波,等.基于LSTM模型的无袖带血压测量方法研究[J].机电工程技术,2023,52(2):72-76.

　　JIANG Z Y,ZHAO Y B,ZHAO J B,et al.Method on cufffree blood pressure measurement based on lstm model[J].Mechani⁃cal&Electrical Engineering Technology,2023,52(2):72-76.