摘要：针对传统机械臂在轨迹规划上工作效率低、运动过程中平稳性不佳和规划算法不够智能化等问题，提出了一种基于改进型粒子群算法对机械臂进行时间最优轨迹规划的策略。该方法通过引入自适应调整惯性权重和非线性动态学习因子的方法来对粒子群算法进行改进优化，采用3-5-3多项式函数构成机械臂在工作空间中的插值曲线轨迹，以时间最优为目标，将机械臂关节速度作为约束，并在寻找最优时间的迭代过程中考虑了适应度值因素，从而完成对机械臂运动轨迹的时间最优规划。通过仿真软件MATLAB进行实验，结果表明，所提改进粒子群算法优化后的轨迹相比于传统粒子群算法具有更快的收敛速度，其总运动时间减少52%，在保证机械臂平稳运动的同时，明显缩短了机械臂的运行时间。

　　关键词：机械臂；粒子群算法；时间最优；轨迹规划

　　0引言

　　机械臂因具有良好的空间灵活性和高效率、高精准等特点，而在现代工业自动化生产行业被广泛应用，能够替代人工完成如搬运、码垛、焊接等复杂危险工作[1]。轨迹规划对实现机械臂的精准轨迹控制起着至关重要的作用，对机械臂的工作效率、能耗和运动流畅性等方面具有重大影响[2]。针对机械臂运动进行高效合理的时间最优轨迹规划，可有效缩短其运动执行时间，从而延长机械臂的使用寿命、提高运行效率，降低生产成本，因此机械臂时间最优轨迹规划仍然是一个被广泛研究的课题[3，4]。

　　为了进一步促进工业机械臂的高效化和智能化发展，国内外学者对机械臂的轨迹规划这一热点领域展开了深入研究。EkremÖzge等[5]将粒子群算法和五阶插值曲线结合，得到更佳的时间最优轨迹曲线和机械臂关节随时间变化的运动信息，实现时间最优。张蕾等[6]采用七次多项式插值对机器人各个关节进行了轨迹规划研究，实验验证了在机器人运动过程中运动平稳且保持连续，得到的关节速度、加速度度随时间变化曲线平滑，无突变。周明月等[7]提出一种利用引入莱维飞行和正弦余弦算法的蝴蝶优化算法对运动轨迹进行时间优化，提高了寻优精度，保证了机械臂的平稳运动。汤兆平等[8]使用混沌映射初始化种群，动态调整权重和收敛因子的方式改进鲸鱼算法用于优化机械臂运动轨迹，提高了算法收敛速度和求解精度。马龙等[9]提出了一种基于改进鸡群优化算法的机械臂轨迹规划方法，以时间和冲击视为优化目标，达到了在降低机械臂运动时冲击的同时缩短了运动时间的目的。黄超等[10]在传统粒子群算法的基础上，让学习因子在迭代的过程中动态改变，在3-5-3多项式插值函数曲线的基础上，实现了对机械臂运动轨迹的优化，缩短了运动时间，但收敛速度较慢。王炳祺等[11]对传统的粒子群算法的收缩因子进行了改进，并根据遗传算法中的变异现象，在粒子群算法中引入变异因子，减小了搜索最优解时陷入局部最优的概率。虽然机械臂轨迹规划方面已有大量研究，但是仍然面临着多项式插值阶次单一或较高、计算复杂以及采用的优化算法存在收敛速度慢、容易早熟等问题。

　　综上所述，本文针对上述机械臂轨迹规划研究过程中存在的不足，提出了一种改进粒子群算法，与传统粒子群算法采用固定的惯性权重值和学习因子值不同，该改进算法通过在迭代过程中自适应调整惯性权重和学习因子的数值，兼顾了在全局和局部二者的搜索能力，使收敛速度得到显著提升。以时间最优为目标，用改进粒子群算法对按3-5-3多项式分段规划的机械臂轨迹进行优化，进而获得机械臂的最佳时间轨迹，大幅减少了机械臂的运行时间，验证了该方法的有效性和优越性。

　　1机械臂建模和多项式插值

　　1.1机械臂运动学建模

　　机械臂运动学分析是研究机械臂轨迹规划的基础[12]，本文以轻型工业协作机器人UR5e为研究对象，该机器人具有6个旋转关节自由度，能够承受5 kg的额定载荷，工作可达的最大半径范围为850 mm，机器人三维模型如图1所示。

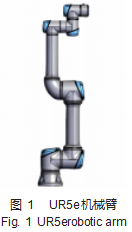
　　根据机器人学连杆坐标系建立方法，通过D-H参数法建立机械臂运动学模型[13]，D-H参数如表1所示。

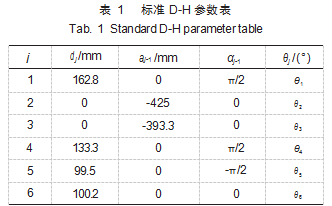
　　1.2构造3-5-3多项式插值函数

　　在机械臂的工作空间中，选取起始点、第1个中间点、第2个中间点和终止点4个点来构成机械臂的运动轨迹，对这4个点对应的关节角度进行求解，可获得机械臂顺利完成规划所需的运动信息。本文采用3-5-3混合多项式插值进行轨迹规划设计，多项式插值函数的公式如下：
      

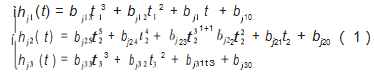
　　式中：hj1(t)、hj2(t)和hj3(t)分别为机械臂第j个关节在第一段、第二段和第三段的轨迹；bjic代表第j个关节在第i段轨迹对应的c次多项式系数；ti（i=1，2，3）为第i段轨迹的运动时间。

　　在已知4个插值点的各关节角度条件下，插值生成的轨迹还应满足以下约束条件：

　　（1）在初始时刻和结束时刻处对应的关节速度和加速度为0；

　　（2）在第一个中间点和第二个中间点处对应的速度和加速度连续。

　　在满足以上约束条件的情况下，可以求解得到3-5-3多项式的各个系数：
        
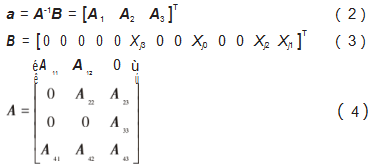
         式中：
        

　　2目标函数的选取

　　本文的研究内容是利用改进粒子群算法以寻求时间最短为优化目标，选择最优的时间让各个关节完成运动。机械臂的三段运动轨迹由tj1代表第1段轨迹的运动时间，tj2代表第2段时间，tj1代表第3段时间，所用总时间用T表示，故目标函数定义为：

　　T=tj1+tj2+tj3（5）

　　考虑到在真实环境中，机器人关节由伺服电机驱动，其关节速度往往有安全工作范围值，于是设置如下速度约束条件：
      

　　式中：Vji代表第j个关节的第i段瞬时速度；Vmax代表最大速度。

　　3改进粒子群算法

　　3.1标准粒子群算法

　　标准粒子群算法是群体智能算法中的一种经典算法，有着参数少、结构简单和搜索范围广等优点[14]。该算法是受到鸟群觅食这一自然行为的启迪，首先明确设立种群粒子的数目，通过种群中所有个体在d维的目标空间中搜索最优解，然后每个个体之间引导和进行信息共享并不断更新迭代，直到寻找到群体的最优值[15-16]，其表达式为：
       

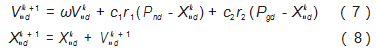
　　式中：n为粒子种群中的第n个粒子；k为当前的迭代次数；ω为惯性权重；c 1、c2为学习因子；r 1和r2为取值为［0，1］之间的任意值；P nd为种群中第n个粒子在d维空间中搜寻到的局部最佳位置；Pgd为种群中第n个粒子在d维空间中搜寻到的全局最佳位置；Vd和Xd分别为第n个粒子在第k次迭代时的速度和位置。

　　3.2改进型粒子群算法

　　在粒子群算法中惯性权重ω和学习因子c的取值对粒子搜索能力和迭代收敛速度有着重要的影响因素[16]。在传统的粒子群算法中ω、c 1、c2取值均为常数，这导致粒子在搜索过程中的位置变化缺乏随机性，不利于寻找全局最优，迭代不易收敛。如果ω取一个较大的固定值，算法全局搜索能力强，但收敛速度较慢且精度不高。如果ω取一个较小的固定值，算法局部搜索能力得到提升，但易早熟收敛[17]。为了避免这种情况，目前主流的策略[18-22]对惯性权重值采用线性递减的方法，使惯性权重在一定区间范围内随着迭代次数增加单调递减，来实现对ω的调整。

　　常用的在一定范围内使惯性权重线性递减的方法对粒子群算法避免陷入局部最优陷阱有一定帮助，但是在迭代搜寻的过程中如果得到相比之前更好的适应度值，惯性权重仍然会随迭代次数保持递减的趋势。为了避免这一缺陷，本文提出了一种能随迭代次数自动变更权重值的优化策略来替代传统算法的固值权重，并加入了粒子适应度值因素，以避免在粒子搜寻迭代过程中产生的最佳适应度值被遗漏。自适应调整惯性权重的表达式为：
        

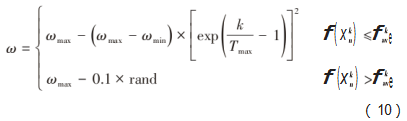
　　式中：ωmax和ωmin分别为惯性权重为最大值和最小值；Tmax为最大迭代次数；rand为（0，1）之间的随机数；

　　f(x)为目前搜索粒子的适应度值；fae为第k次迭代时，全部粒子的平均适应度。

　　本文针对算法中的学习因子采用非线性动态学习因子的策略进行改进。在粒子搜索迭代初期采用较大的c 1值和较小的c2值，随着迭代次数的增加，c 1不断减小，c2不断增加，从而提高搜索效率，避免陷入局部最优。改进后的学习因子规则为：
       

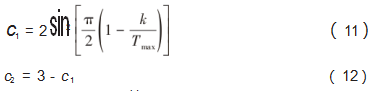
　　改进后粒子群优化算法的轨迹规划流程图如图2所示。

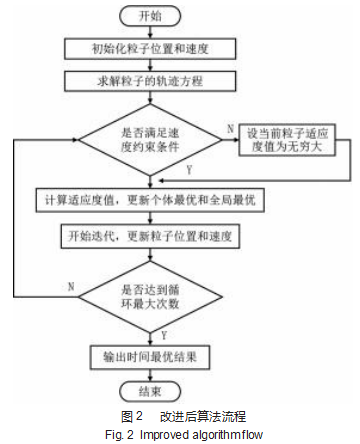
　　4仿真验证与结果分析

　　本文以UR5e机械臂实验对象，利用MATLAB软件进行实验仿真，验证所提出的算法的正确性和可用性。实验在3-5-3插值多项式基础上，使用上述改进粒子群算法优化机械臂各关节完成任务轨迹。在机械臂工作的三维空间中，寻找4个可以到达的点构成机械臂在工作空间中的运动路径，并作为机械臂在空间中的插值点，设置起点X1、第1个中间点X2、第2个中间点X3和终点X4的位置坐标分别为（590，305，373）、（43，481，477）、（-205，415，-190）、（-616，32，222），并逆运动学求解得到各关节在以上4个插值点的角度，相邻插值点之间的间隔时间均为3 s，对应插值点的关节角度如表2所示。设置粒子种群数目N为50，最大迭代次数Tmax为100，ωmax=0.9，ωmin=0.2，关节最大运动速度Vmax=180(°)/s。在标准粒子群算法中通常取ω=0.9，c 1=c2=2。

　　为验证改进粒子群算法的优越性，将机械臂第一关节的适应度值与迭代次数的关系作图，用改进粒子群算法对关节进行了时间最佳优化，并将用基本粒子群算法和改进粒子群算法的迭代过程进行比较，其收敛曲线对比如图3所示。

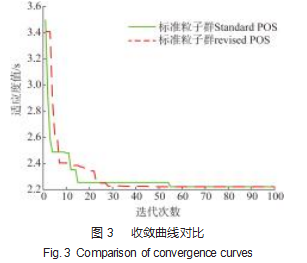
　　根据图3得到的仿真结果可知：采用改进粒子群算法在粒子种群中只需要经过28次迭代搜寻就得到最佳适应度值，和传统的粒子群算法55次迭代才收敛最佳适应度值对比，搜索效率提升了49%。由此可见改进粒子群算法的搜索能力和迭代到达最佳适应度值的速度有显著提升。

　　在经过改进算法优化后，得到各关节在各个阶段的运行时间，结果见表3所示。

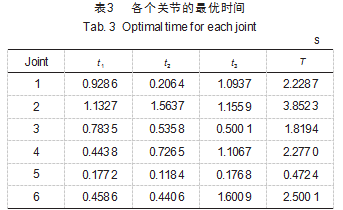
　　为确保机械臂各关节都能够完成规划的运动动作，需要选取各关节在各段时间中的最大值，根据表3得到，t 1=1.132 7 s，t2=1.563 7 s，t3=1.600 9 s，通过计算可以得出机械臂在这3段轨迹中的运动总时间为4.297 3 s，对比于机械臂运动时间的初始值9s运动时间减少了约52%。说明机械臂各关节在通过改进粒子群算法的有效优化下可以缩短机械臂总工作时间，提升工作效率。通过仿真得到机械臂优化前后各关节位置、速度和加速度的曲线如图4~9所示。

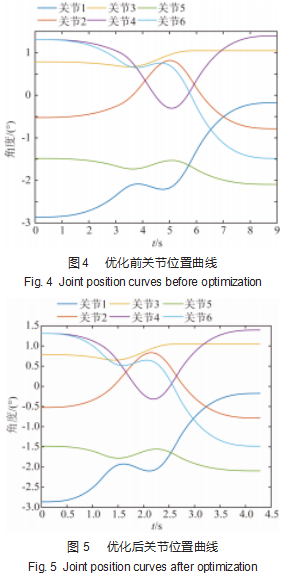
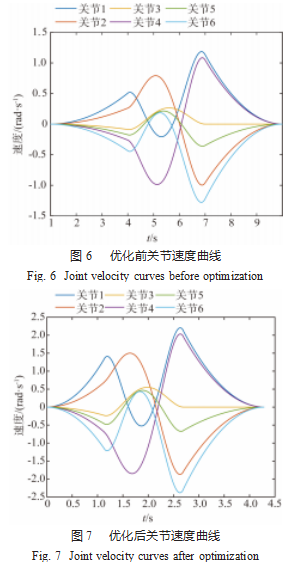
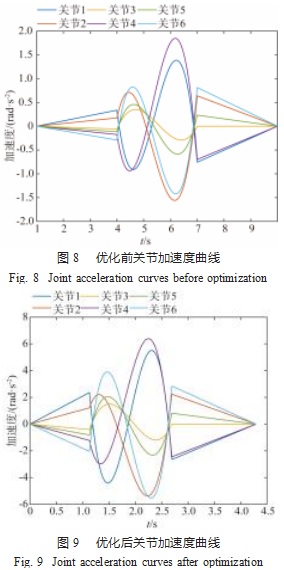
　　根据图4~9可知：优化后机械臂各关节的位移、速度和加速度变化曲线平滑，机械臂在通过所有的预设运动轨迹后，其运动时间明显减少并满足平稳运行要求。运动过程中各关节在起始点的速度、加速度为0，在终止点处速度、加速度均为0，并满足各个关节约束条件。实验结果表明，经过改进算法对机械臂轨迹规划优化后，机械臂完成运动轨迹的时间明显缩短，运动过程中满足约束条件的同时，速度和加速度的峰值得到提高。

　　5结束语

　　文中选择UR5e机械臂作为研究模型，探讨了关于机械臂轨迹规划的时间最优问题，提出了一种改进粒子群算法来对所生成轨迹进行时间优化。该改进方法在根据迭代次数自适应变化调整数值的惯性权重和动态变化的学习因子的基础上，加入粒子适应度值因素，改善了传统粒子群算法收敛速度慢、易早熟和遗漏最佳适应度值的问题，确保粒子在全局搜索和局部搜索中都有着较好的表现。通过对仿真实验得到的数据分析证明，采用改进粒子群算法所用的时间比规划前降低了52%，并与传统粒子群算法对比迭代速度明显更快，机械臂的工作效率显著提高，应用的改进轨迹规划算法的有效性也得到了证实。

　　[1]李黎,尚俊云,冯艳丽,等.关节型工业机器人轨迹规划研究综述[J].计算机工程与应用,2018,54(5):36-50.

　　LI L,SHANG J Y,FENG Y L,et al.Research of trajectory plan⁃ning for articulated industrial robot:a review[J].Computer Engi⁃neering and Applications,2018,54(5):36-50.

　　[2]董理,杨东,鹿建森.工业机器人轨迹规划方法综述[J].控制工程,2022,29(12):2365-2374.

　　DONG L,YANG D,LU J S.Trajectory planning methods for in⁃dustrial robots:a review[J].Control Engineering of China,2022,29(12):2365-2374.

　　[3]施祥玲,方红根.工业机器人时间-能量-脉动最优轨迹规划[J].机械设计与制造,2018(6):254-257.

　　SHI X L,FANG H G.Time-energy-jerk optimal planning of in⁃dustrial robot trajectories[J].Machinery Design&Manufacture,2018(6):254-257.

　　[4]姜昊.六自由度机械臂轨迹规划仿真研究[D].沈阳:沈阳理工大学,2023.

　　[5]Özge E,Bekir A.Trajectory planning for a 6-axis robotic arm with particle swarm optimization algorithm[J].Engineering Appli⁃cations of Artificial Intelligence,2023,122.

　　[6]张蕾,田瑜,李鹏飞,等.四自由度机器人抓取运动目标建模与轨迹规划[J].制造业自动化,2017,39(12):44-48.

　　ZHANG L,TIAN Y,LI P F,et al.Modeling and trajectory plan⁃ning of four-DoF robot grasping moving target[J].Manufacturing Automation,2017,39(12):44-48.

　　[7]周明月,周明伟,刘桂岐,等.基于改进蝴蝶算法的机械臂时间最优轨迹规划[J].计算机科学,2023,50(S2):119-126.

　　ZHOU M Y,ZHOU M W,LIU G Q,et al.Time optimal trajectory planning of manipulator based on improved butterfly algorithm[J].Computer Science,2023,50(S2):119-126.

　　[8]汤兆平,孟鑫,孙剑萍,等.基于改进鲸鱼优化算法的码垛机器人时间最优轨迹规划[J].科学技术与工程,2024,24(14):5882-5891.

　　[9]马龙,李长勇,司庆.基于改进鸡群优化算法的机械臂轨迹规划[J].组合机床与自动化加工技术,2023(12):61-66.

　　MA L,LI C Y,SI Q.Trajectory planning of manipulator based on improved chicken swarm optimization[J].Modular Machine Tool&Automatic Manufacturing Technique,2023(12):61-66.

　　[10]黄超,茅健,马丽,等.基于改进粒子群算法的时间最优机械臂轨迹规划[J].上海工程技术大学学报,2020,34(3):238-246.

　　HUANG C,MAO J,MA L,et al.Time-optimal trajectory plan⁃ning for manipulator based on improved particle swarm optimi⁃zation algorithm[J].Journal of Shanghai University of Engineer⁃ing Science,2020,34(3):238-246.

　　[11]王炳祺,石敏,朱登明,等.基于改进型粒子群算法的机械臂轨迹规划[J].组合机床与自动化加工技术,2022(11):44-47.

　　WANG B Q,SHI M,ZHU D M,et al.Trajectory planning meth⁃od of manipulator based on improved particle swarm optimiza⁃tion algorithm[J].Modular Machine Tool&Automatic Manufac⁃turing Technique,2022(11):44-47.

　　[12]赵寒冰,罗欣,钟启明,等.基于法向同步误差补偿的机械臂多轴同步控制[J].微电机,2023,56(2):61-65.

　　ZHAO H B,LUO X,ZHONG Q M,et al.Multi-axis Synchroni⁃zation Control of Manipulator Based on Normal Synchronization Error Compensation[J].Micromotors,2023,56(2):61-65.

　　[13]彭光宇,董洪波,马斌.两种DH模型的机器人运动学建模对比研究[J].机械研究与应用,2019,32(6):62-65.

　　[14]江鸿怀,金晓怡,邢亚飞,等.基于粒子群优化算法的五自由度机械臂轨迹规划[J].机械设计与研究,2020,36(1):107-110.

　　[15]吴静,罗杨.动态调整惯性权重的粒子群算法优化[J].计算机系统应用,2019,28(12):184-188.

　　[16]Guedes J J S D,Paulo J L M D S,Veronica T.Occlusion-robust method for RGB-D 6-DOF object tracking with particle swarm optimization[J].Expert Systems with Applications,2021,174.

　　[17]朱茂桃,刘欢,吴佘胤,等.混合策略改进的粒子群算法[J].重庆理工大学学报(自然科学),2024,38(1):110-121.

　　[18]黄开启,陈翀,刘展飞.基于改进粒子群算法的凿岩机械臂轨迹规划[J].中国工程机械学报,2022,20(5):401-406.

　　HUANG K Q,CHEN C,LIU Z F.Rock drilling arm trajectory planning based on improved particle swarm optimization algo⁃rithm[J].Chinese Journal of Construction Machinery,2022,20(5):401-406.

　　[19]吴庆宗,胡兴柳,周智慧.基于改进粒子群算法的六自由度机械臂轨迹优化[J].盐城工学院学报(自然科学版),2023,36(4):41-47.

　　WU Q Z,HU X L,ZHOU Z H.Trajectory optimization of 6-dof manipulator based on improved particle swarm algorithm[J].Journal of Yancheng Institute of Technology(Natural Science Edition),2023,36(4):41-47.

　　[20]段倩倩,辛绍杰.基于改进混合粒子群算法的机器人轨迹规划[J].机床与液压,2022,50(17):50-56.

　　DUAN Q Q,XIN S J.Robot trajectory planning based on im⁃proved hybrid particle swarm optimization[J].Machine Tool&Hydraulics,2022,50(17):50-56.

　　[21]桓茜,陈宇,王伟.外骨骼助行机器人关节运动轨迹研究[J].自动化仪表,2024,45(5):73-76.

　　HENG X,CHEN Y,WANG W.Research on Joint Motion Tra⁃jectory of Exoskeleton Assisted Walking Robot[J].Process Auto⁃mation Instrumentation,2024,45(5):73-76.

　　[22]朱浩,赵清海,郑群锋,等.改进粒子群算法的自动充电机械臂时间最优轨迹研究[J].机械科学与技术,2024,43(03):423-429.ZHU H,ZHAO Q H,ZHENG Q F,et al.Exploring time-opti⁃mal trajectory of automatic charging manipulator with improved particle swarm optimization algorithm[J].Mechanical Science and Technology for Aerospace Engineering,2024,43(3):423-429.