摘要：通过正交实验方法对儿童烘干机的风机系统性能进行优化，以提高烘干效率，降低能耗，减少噪声。首先，根据正交实验理论设计了部分因子正交实验方案，对影响风机系统性能的关键因素进行研究，包括风轮外径、风轮长度、蜗壳出风口宽度等。然后，通过实验实施与数据采集，获得了大量风机系统性能数据。接着，利用统计学方法对实验数据进行了详细分析，找出了影响风机性能的关键单因子和两因子交互作用。根据实验结果分析，单因子风轮外径和风轮长度对风机性能有显著影响，同时两因子交互作用也对性能产生明显影响。根据实验数据分析，建立了以主要影响因素为主的数学模型，为优化设计提供了理论依据。最后，根据实验结果建立了数学模型，并进行了计算机建模和优化设计，成功提高了风机系统的效率，降低了能耗，并保持了产品尺寸的紧凑性。优化后的风机系统具有更高的效率、更低的能耗和更紧凑的产品尺寸，为儿童衣物烘干机的设计提供了有益的参考。

　　关键词：正交实验设计；儿童织物烘干机；风机系统；优化设计

　　0引言

　　风机系统作为儿童衣物烘干机的核心组成部分，其性能直接决定了烘干机的整体效率、能耗及使用寿命。随着科技的进步和消费者对产品性能要求的提高，对风机系统性能的研究和优化显得尤为重要。本文旨在通过正交实验设计，系统地分析影响风机系统性能的关键因素，并构建数学模型和计算机模拟模型，以优化风机系统的设计，提高烘干机的整体性能。

　　在国内外研究方面，已有大量学者对风机系统的性能进行了深入研究。他们通过理论分析、实验研究和数值模拟等方法，探讨了风机系统的流场特性、优化设计和控制策略等问题。然而，对于特定类型的衣物烘干机，尤其是儿童衣物烘干机，其风机系统的性能研究相对较少。因此，本文的研究具有重要的理论意义和实际应用价值。

　　在研究方法上，本文采用了正交实验设计的方法，通过选取具有代表性的风机系统参数，进行系统的实验测试和数据分析[1]。通过拟合最小二乘法、拟合两水平筛选、高斯过程模型等方法对实验数据进行统计分析，评估风机系统的综合性能，并找出影响性能的关键因素。同时，本文还结合了流体力学相关知识和离心式风机扇叶工作原理[2],对实验结果进行了深入的分析和讨论。

　　预期的结果方面，本文希望通过正交实验设计和数据分析，构建出能够准确描述风机系统性能的数学模型。同时，通过计算机模拟建模，对风机系统的细节部分进行进一步优化设计，以提高风机系统的效率和降低能耗。最终为儿童衣物烘干机及同类型产品的设计优化提供一种新的思路和方法，推动相关领域的技术进步和产业发展。

　　综上所述，本文的研究具有重要的理论意义和实际应用价值。通过对风机系统性能的关键因素进行正交实验设计和优化设计，可以提高儿童衣物烘干机的整体性能，降低能耗，满足消费者对产品性能的要求。同时，本文的研究成果也为进一步研究提供了理论依据和实验数据支持，有助于推动风机系统性能研究的深入发展。

　　1正交实验设计原理

　　实验设计(Design of Experiments,DOE[3])也被称为试验设计，就是对实验进行科学合理的安排，以达到最好的实验效果。正交实验设计是一种多因素、多水平的实验设计方法，根据正交性从全面实验中挑选出部分有代表性的点进行试验，这些有代表性的点具备均匀分散、齐整可比的特点。通过正交表来安排实验，使得每个因素在每个水平上都只出现一次，且各因素之间的搭配是均匀的[4]。这种设计方法能够最大限度地减少实验次数，同时保证实验结果的准确性和可靠性。但当实验涉及的因子数量大于4个时，因子间可能会出现交互作用影响，为分析这部分交互影响，试验工作量将会变得很大，甚至难以实施。本文使用部分因子实验设计，即试验者根据试验的因素数，因素的因子水平及是否具有潜在的交互作用等需求从全面试验中根据正交表的正交性挑选出部分有代表性的点进行试验。进而用最小的试验次数达到最大化的因子因素分析水平。

　　本文将影响吹风系统性能的关键因素作为正交实验设计的因素，包括风扇转速、风口数量、风口布局等。通过设计正交实验，可以系统地分析这些因素对吹风系统性能的影响，并找到最优的设计方案，并为构建特定条件下风轮模型提供理论和实验数据基础。

       2实验设计与实施

　　2.1关键因子与水平的选择

　　根据风机系统的特点和实际需求，按照传热学相关理论[5],对现有产品风机系统进行分析并构建风机系统思维导图和产品图进行深入分析，在马达功率选定的基础上对影响热传导效率和风机流量效率的潜在关键因子[6]进行排序后，选择了风轮叶片数量X1、风轮外径X2、风轮内径X3、风轮长度X4、风轮叶片出口角度X5、风轮叶片入口角度X6、蜗壳出风口宽度X7和蜗壳长度X8等关键因素作为正交实验设计的因子。根据产品的使用环境对每个因子设置了两个水平，以覆盖可能的取值范围，如表1所示。

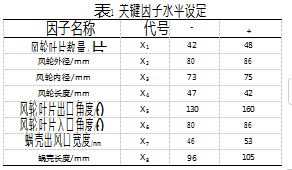
　　同时利用正交实验对因子间的交互影响进行分析。目的是为了分析得到关键因子（或因子交互）与风机性能指标间的关系[7],并建立如式(1)的数学模型。

　　Y=f(x)+NNoise(1)

　　式中：Y为风机性能指标；f(x)为关键因子对风机性能指标的影响；NNoise为非关键（环境）因素影响[8]。

　　2.2正交实验的构建

　　根据选定的因素和水平，如按照全因子实验进行的话，实验的配置和样品数量需要256组，实验周期和实验成本都将非常巨大，并且在现实中多因子交互影响往往远远弱于单因子或两因子交互对于结果的影响[9],因此根据正交实验理论，对正交实验中的配置点进行深入分析，对于潜在两因子交互影响进行相应研究，保证每个因素在每个水平上都只出现一次，且各因素之间的搭配是均匀的，在全因子正交表中选择对应点进而构建16组配置的部分因子正交实验[10],同时实验顺序采用完全随机的顺序以避免实验顺序带来的误差影响，正交实验模型树如图1所示。

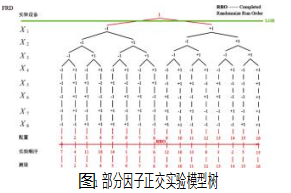
　　2.3实验实施与数据采集

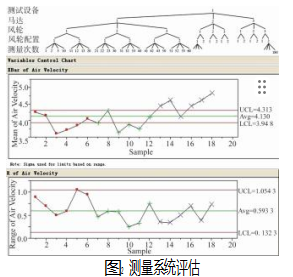
　　在进行正式实验之前，对风动实验室的测量系统进行了测量系统评估(MSE)。

　　参考相关统计学方法进行取样和实验排布[11]如图2所示，根据测量系统评估原则对180组数据进行相应统计学分析，最终测量系统评估数据证明该测量系统的重复性和一致性[12]完全可以满足研究需要。

　　3实验结果与分析

　　在前述测量系统上，依照正交实验模型树的配置和实验顺序进行了多组实验。在每组实验中，记录吹风系统的出口风速，压力和流量等数据。将各组实验数据进行汇总，得到不同因素水平组合下的流量、压力和风速等风机系统性能数据，根据拟合最小二乘法、拟合两水平筛选、高斯过程模型等方法对这些数据进行同统计学分析[13],评估风机系统的综合性能，并找出影响性能的关键因素。实验数据分析如图3所示。

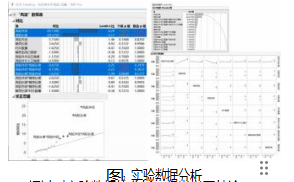
　　通过对实验数据的分析，得出以下结论。

　　(1)单因子风扇外径和风轮长度对风机系统性能有显著影响。随着风轮外径和风轮长度的风速更快分布更加均匀，风量更大，烘干时间将显著缩短，但对空间的要求也更高，产品尺寸将增加。因此，在选择风轮外径和风轮长度时需要在产品的外尺寸间找到平衡点。

　　(2)存在两因素交互作用对风机性能有明显影响，因实验采取的是部分因子实验设计，根据8因子2水平16次测试的部分因子正交实验设计的配置原理，数据分析中两个因子交互影响结果其实是四组两因子交互作用的重叠，因此单纯从实验数据的统计学分析上无法分辨到底是哪两个因子交互作用的影响。根据流体力学相关知识和离心式风机扇叶工作原理分析最大的两因子交互作用可能是风轮叶片出口角度×蜗壳出风口宽度、风轮叶片出口角度×蜗壳长度、风轮叶片出口角度×风轮叶片入口角度[14-15]。由此可以看出风轮叶片角度和涡轮尺寸布局对风机系统性能的影响较为复杂。合理地设定风轮叶片角度和涡轮尺寸布局可以提高风速分布的均匀性和烘干效率，但具体的布局方式需要根据产品的结构和使用场景来确定。

　　通过分析正交实验数据结果，得到主要影响因子（单因子和两因子交互）与风机性能之间的关系，以风量为例，如式(2)所示。

　　Y=254+24.75·X2-20.38·X4-8.88·X5·X7-8.75·X5·X8-7.63·X5·X6(2)

　　对建立的数学模型与实际测试数据进行进一步地拟合分析，如图4所示，该数学模型的拟合度非常好，因此该数学模型为风机系统的优化设计指明了设计方向也为后面的计算机模拟建模提供了理论和实验基础。

　　4建模模拟与效果分析

　　根据前述部分因子正交实验结果和由此建立的数学模型，对现有的风机系统进行优化设计，将风轮外径、长度以及涡轮的开口尺寸和布局方式都进行了相应的优化，并将优化前后的风机系统进行计算机建模，对细节部分的流速和压强进行全面分析，优化风机系统的细节部分，进一步减少风机系统能量损失，提高系统效率和整体性能。根据实际情况，建模分析中基于如下假设[16]:(1)假设流量稳定且不可压缩；(2)利用运动参考系法(MRF)对风机进行了仿真；(3)采用了Spal-art-Allmaras湍流模型。

　　建模模拟结果如图5所示，优化后的风机系统表现出以下优点。

　　(1)风机系统效率显著提高。优化后的风机系统使得风机流量大幅度提高，相较优化前产品风机效率提升了接近80%,从而提高了烘干效率。在相同的烘干时间内，可以更加有效地去除儿童织物中的水分。

　　(2)能耗降低。优化后的风机系统使得风速分布更加均匀，大幅度减少在蜗壳内的紊流降低能量损失，同时也大幅度减少了风机系统的噪声，优化后的吹风系统在保持高效烘干的同时，降低了能耗。这有助于减少家庭用电成本，同时符合节能减排的环保要求。

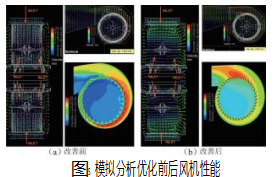
　　(3)产品尺寸更加紧凑。优化后的风机系统采用了更加合理的风轮和蜗壳设计，在提高整体性能的情况下，并未增加产品的整体尺寸。使得产品整体尺寸更加紧凑并更具空间感。

       5结束语

　　本文通过对儿童衣物烘干机的风机系统性能关键因素进行正交实验设计，系统地分析了这些因素对吹风系统性能的影响，构建数学模型和计算机模拟模型，并找到了最优的设计方案。通过构建特定条件下风轮模型，为风机系统的优化设计指明了方向，并为计算机模拟建模提供了理论和实验基础。实验结果表明，单因子风扇外径和风轮长度对风机系统性能有显著影响，而两因素交互作用对风机性能也有明显影响。通过优化设计，风机系统效率显著提高，能耗降低，产品尺寸空间更加紧凑。本文的研究成果为儿童衣物烘干机及同类型产品的设计优化提供了一种新的思路和方法，有助于提高风机系统的性能和降低能耗，符合节能减排的环保要求。也为进一步研究提供了理论依据和实验数据支持，具有重要的理论和实际应用价值。

　　参考文献：

　　[1]Patrick D T O Connor.试验工程—成本有效的设计、研制和制造指南[M].北京：电子工业出版社，2005.

　　[2]昌泽粥．轴流式通风机实用技术[M].北京：机械工业出版社，2005.

　　[3]刘文卿．实验设计[M].北京：清华大学出版社，2007.

　　[4]Douglas C Montgomery.实验设计与分析（英文版·第6版）[M].北京：人民邮电出版社，2008.

　　[5]章熙民，任泽霈，梅飞鸣．传热学[M].北京：中国建筑工业出版社，2009.

　　[6]潘小勇．流体力学与传热学[M].南昌：江西高校出版社，2019.

　　[7]Rodrigues F J,Sequeira A.Mathematical Topics in Fluid Me-chanics[M].CRC Press,2020.

　　[8]Donald J Wheeler.Understanding Variation[M].SPC Press,2020.

　　[9]Richard A Johnson,Dean W Wichern.实用多元统计分析（英文版·第6版）[M].北京：清华大学出版社，2008.

　　[10]庞超明，黄弘．试验方案优化设计与数据分析[M].南京：东南大学出版社，2018.

　　[11]赵选民．试验设计方法[M].北京：科学出版社，2006.

　　[12]何晓群，刘文卿．应用回归分析[M].北京：中国人民大学出版社，2007.

　　[13]王培刚，梁静，张刚鸣．多元统计分析与SAS实现[M].武汉：武汉大学出版社，2020.

　　[14]Bryan L M.Fluid Mechanics[M].Tritech Digital Media,2018.

　　[15]陈锡勇．离心式通风机的安装及使用维护的分析[J].机电工程技术，2014,43(8):147-149.

　　[16]凌桂龙.Fluent 2020流体计算从入门到精通[M].北京：电子工业出版社，2021.