摘要：HXD1D型电力机车轮对轴箱装置的正常运转是保证机车安全运行的必要条件，在机车轴承检修中，需要将轴承进行全部分解并清洗后才能确定轴承各部件发生故障与否，这使得检修时间过长，增加检修成本。为实现高置信度的轮对轴箱装置运行状态在线监测和早期故障预警，采用变分模态分解算法将原始信号分解为多个独立频率分量，同时计算各分量多尺度散布熵，以实现特征提取。随后，基于最大相关最小冗余算法计算得到多维特征向量之间的冗余程度和相关程度，实现正交特征值的定量筛选。随后将特征向量输入至长短时记忆网络(LSTM)中输出缺陷识别类型。为消除各算法超参数对模型精度的影响，采用贝叶斯优化算法对变分模态算法、散布熵和LSTM模型的超参数寻优，实验结果表明相较于随机参数模型，所提模型的缺陷识别精度提升了15%左右。

　　关键词：轴箱轴承；故障诊断；贝叶斯优化；特征集合优选；深度神经网络

　　0引言

　　随着“一带一路”倡议的深入推进，中国与沿线国家铁路基础设施建设合作在区域互联互通、经济增长以及国际合作等方面获得成效，在共建跨国铁路网络、促进各国贸易往来等方面取得骄人成就[1]。相应地，加强铁路运行设备的维护，实现智能化、数字化和自动化的电力机车运维，将为铁路系统安全提供技术保障[2]。其中，机车轴箱轴承在长期高速、重载运行环境下，容易出现磨损、疲劳、裂纹等故障，严重时将引发安全事故[3]。

　　近年来，随着智能化信息技术、小型化微传感器技术以及高速化通信技术的快速发展，基于振动信号中蕴藏的丰富信息，数据驱动的轴承故障诊断框架得到研究人员的广泛关注，并在识别准确度和诊断效率方面取得诸多成果。早期研究立足于振动信号时频域分析，一系列时序频域分析算法，如短时傅里叶变换、小波变换(Wavelet Transform,WT)、经验模态分解(Empirical Mode Decomposition,EMD)及其改进模型[4]、变分模态分解(Variational Mode Decomposition,VMD)[5],通过将原始信号分解为多个具有独立频段的固有模态分量，上述方法在处理非线性复杂轴承振动信号时，取得了良好鲁棒性。例如，王发令等[6]提出采用WT处理振动数据，随后采用奇异谱熵提取特征向量，采用元启发算法优化极限学习机超参数，实现了少故障样本下的滚动轴承故障诊断。张韦［7］、谢平波［8］和杜文辽［9］等人基于EMD及其衍生改进算法对振动信号进行预处理，相较于WT，EMD能够更好地突出信号局部特征，在时频聚焦方面表现较优。然而，其存在模态混叠、端点效应和包络过充等问题［10］，其分解效果取决于专业人员的先验知识。

　　VMD以维纳滤波器、希尔伯特变换和频率混合为基础的变分求解问题，能够有效避免模态混叠和端点效应，具备良好的分解鲁棒性和稳定性，从而更准确地提取特征信息。

　　在特征提取方面，诸多学者基于熵作为振动信号非线性动力学指标，旨在提取振动信号种的非线性故障特征参量［11］。在研究过程中，学者们发现单一尺度的熵值，无法准确提取信号中的复杂特征，并影响诊断模型精度。为此，提出多尺度熵，通过将时间序列多尺度化，量化熵与尺度因子之间的关联关系，从而实现序列复杂度动态评估［12］。然而，尺度因子的大小与时间序列长度相关，同时依赖于人工经验，有必要对这一参数进行慎重选择，以保障正交特征量的提取。

　　随着物联网技术迅猛发展，基于数据驱动的机器学习和深度学习方法广泛应用于机械故障诊断。为实现更高精度的缺陷诊断精度，对模型超参数进行优选成为高效的手段。周玉等［13］提出应用长短时记忆网络（Long Short-Term Memory，LSTM）模型实现故障诊断，为提升模型识别精度，提出自适应t分布策略的麻雀搜索算

　　法对其中的隐含层神经元的数量、周期次数、学习率和批量大小值等超参数进行优选。何凯等［14］在应用北方苍鹰算法优化VMD超参数的基础上，进一步采用蜣螂优化算法优化－支持向量机诊断模型超参数，结果表明参数对VMD分解效果以及缺陷诊断精度均有显著影响。吴亚丽等［15］提出包络熵确定VMD最优分解层数以及筛选分量，随后引入粒子群算法对稀疏自编码器的关键参数进行优化，结果表明基于超参数寻优的模型实现了更高的诊断准确率和稳定性。

　　综上所述，现有针对超参数的研究大多数关注于单一算法本身，而未计及整体诊断框架，即各算法超参数未实现同步择优。为此，本文提出基于VMD、多尺度散布熵、最大相关最小冗余（Maximal Correlation MinimizedRedundancy，MCMR）和LSTM的故障诊断框架。同时，应用贝叶斯优化理论，对VMD、多尺度散布熵以及LSTM超参数集进行协同寻优。

　　1基础理论

　　1.1变分模态分解

　　变分模态分解（Variational Mode Decomposition，VMD）是一种自适应且非递归的信号处理与模态变分方法。其突出的优势在于能够自主确定模态分解的最佳数量。这种自适应性体现在它可以根据具体信号序列的特性来灵活设定模态数量。在后续的搜索和求解过程中，VMD能够自适应地识别并匹配每种模态的中心频率和带宽，从而有效分离出固有模态分量。因此，VMD不仅实现了信号的频域划分，还成功提取了给定信号的关键成分，最终求得变分问题的最优解。其工作原理基于信号在时频域上的稀疏性特性，即信号的不同频率成分在特定时间点是稀疏分布的。为了实现信号的分解，VMD通过迭代求解一个优化问题来实现信号的分解，具体步骤如下［16］。

　　（1）假设待分解的信号为x（t），通过迭代求解一组稀疏的频率分量uk（t）和对应的中心频率ωk。

　　（2）则约束优化问题如下：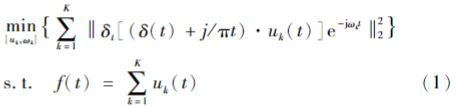

　　（3）通过引入二阶惩罚参数α和增广拉格朗日函数λ（t）得到上式的扩展拉格朗日函数形式：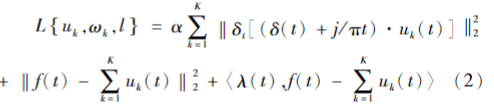

　　（4）基于交替方向乘子（ADMM）迭代算法更新频率分量uk（t）、对应的中心频率ωk和λ（t）。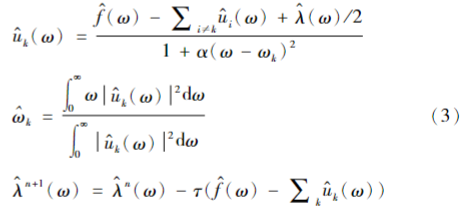

　　（5）重复上述步骤，满足迭代条件时停止优化。

　　上述VMD迭代求解过程中，模态数量K和二阶惩罚参数α通常依据人工经验进行设定，其在一定程度上影响了信号分解精度。

　　1.2最大相关最小冗余算法

　　最大相关最小冗余（Maximal Correlation MinimizedRedundancy，MCMR）算法，旨在优化得到一组特征子集，在最大化特征与目标输出之间的相关性的同时，最小化特征之间的冗余性［17］。给定样本X={x1，x2，…，x n}，F={f1，f2，…，fn}为特征集合，Y为预测值，则各特征参量与预测值之间的相关性采用下式获得：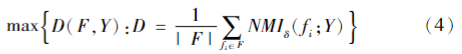

　　此外，冗余性指的是特征之间的相关性，选择具有相似信息的特征会增加模型的复杂度而不增加信息量：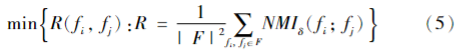

　　为使各特征参量与预测值之间的相关信息最大且各参量之间的冗余信息最小，采用下式得到最优精简特征参量：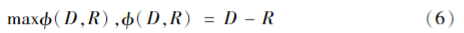

　　通过MCMR对特征集合进行优选，有助于提升故障缺陷识别模型的性能和泛化能力。

　　1.3长短时记忆网络

　　长短时记忆网络（Long Short-Term Memory Network，LSTM）通过在单一神经元基础上引入遗忘门、输入门以及输出门3种门结构来捕捉和记忆序列中的长期信息［18］，并解决传统循环神经网络在训练过程中出现的梯度爆炸问题，如图1所示。其中，Ct为记忆单元，h t为隐藏层，其负责传递信息和记忆到下一个时间步或下一层，以维持序列数据的连续性和一致性。i t为输入门，ft为遗忘门，o t为输出门，x t为输入特征量。LSTM正向传播过程如下式：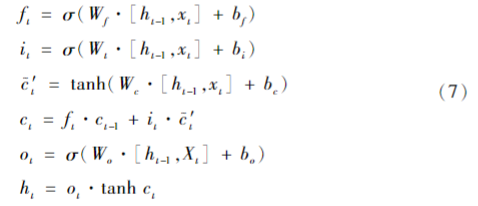

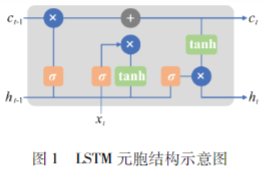
　　1.4贝叶斯优化理论

　　贝叶斯优化的目标是找到全局最优解［19］，为了找到使目标函数最优化的参数，需要提供有效的策略来选择下一个评估点。该策略由采集函数提供，从而在每次迭代中，指导算法搜索最有可能找到最优解的区域。常见的采集函数包括预期改善、上置信界和熵搜索等。上述基于高斯过程模型提供不确定性估计，计算出每个潜在采样点的后验分布，从而指导算法选择下一个评估点。通过多次迭代上述过程，贝叶斯优化能够在有限的样本下高效地搜索最优解，尤其是在处理高维、非线性或噪声较大的问题时表现出色。贝叶斯优化过程如下［20］。

　　（1）初始化代理函数的先验分布。

　　（2）最大化采集函数，并获得下一个评估点：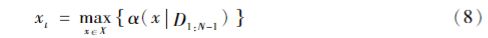

　　式中：D1：N={（x1，f（x1）），（x2，f（x2）），…，（xN，f（xN））}为样本集；x i为决策变量。

　　（3）通过下式获得目标函数值：

　　yt=f（x t）+εt（9）

　　（4）更新代理函数

　　（5）重复（2）~（4）至最大迭代次数。

　　2基于贝叶斯优化变分模态分解与深层网络的故障诊断模型

　　2.1基于V MD和M CMR的轴承故障特征集提取

　　首先采用变分模态分解将原始振动信号x（t）分解为K个固有模态函数uk（t），为了进一步提取得到各分量上的时频统计特征，采用多尺度散布熵对各分量计算不同尺度上的信号复杂度。首先对uk（t）进行正态累计分布积分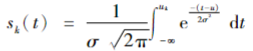随后通过下式将

　　zt=round（c×yt+0.5）（10）

　　其中c即为尺度参数，根据像空间重构将zt映射为m维矩阵z，c={z，z+d，…，z+（m-1）d}，对于每一个尺度参量，采用下式计算多尺度散布熵值：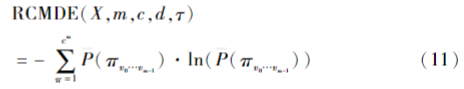

　　式中：πv0…vm-1为散布模式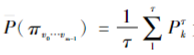为粗粒化序列的散布模式出现的概率的平均值。

　　基于此，原始信号x1×N将转换成特征集合pK×c。随后，基于MCMR算法得到特征集合中各维向量的评估分值。同时，以相邻评分差值最大为特征筛选边界得到优选特征集合（即最大相关最小冗余优化集）。

　　2.2基于贝叶斯优化的故障诊断模型超参数寻优

　　上述特征提取和缺陷诊断模型中包含了大量超参数，在各阶段均对最终的缺陷诊断结果造成影响。变分模态分解算法中的分量个数K、正则化参数α直接影响到信号的分解结果，选择不合适的模态数目可能导致信号过度分解或者不足分解，从而影响到提取的特征的质量。

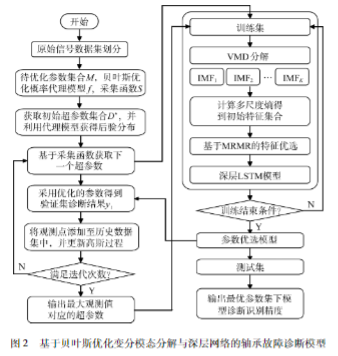
　　正则化参数的选择需考虑平衡信号拟合的光滑度和保留信号细节的能力。多尺度散布熵的尺度参数c则影响着特征集合的冗余程度和整体算法的运行效率；深度LSTM模型各层级中元胞个数N、学习率μ、数据训练批次b将影响到模型的拟合能力、泛化能力以及对测试集的适应能力。因此，有必要在进行特征提取和构建诊断模型时，对各超参数进行统筹优选，以确保模型能够充分捕获到信号的特征并且具有良好的泛化能力，从而得到准确可靠的缺陷诊断结果。完整的算法运行流程如图2所示。

　　3实验设计与分析

　　3.1实验平台

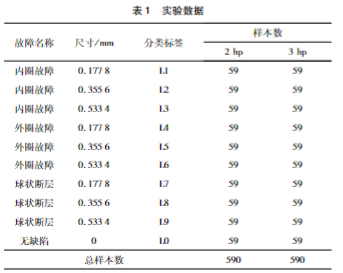
　　HXD1D型电力机车采用免维护的双列圆柱滚子轴承单元[21]。双列圆锥滚子轴承的基本结构包括内外圆环、滚子、保持架和密封装置等组成。内外圆环分别用来承载和定位滚子，通过滚子在内外圆环之间的转动以及与滚道的接触来实现运动传递。滚子的角度布置使得双列圆柱滚子轴承能够承受较大的径向和轴向负荷。保持架用于保持滚子的间距，并确保滚子有良好的运动状态[22]。为验证所提出轴承故障诊断模型对不同工况下滚动轴承故障诊断的性能，本研究基于凯斯西储大学(CWRU)的公开数据集，使用电机负载2hp(1 750 tr/min的电机转速）和3hp(1 730 tr/min的电机转速）下的轴承故障振动数据，并将其划分为训练集和验证集。选取不同尺寸(0.177 8 mm,0.355 6 mm,0.533 4 mm)轴承无缺陷、内圈故障、外圈故障和球状断层缺陷，总样本量为3×2×3×59,即，各样本包含2048个采样点，实验数据具体描述如表1所示。

　　3.2实验结果分析

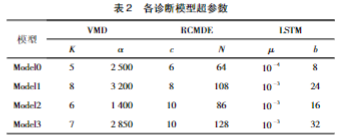
　　为验证基于贝叶斯优化全模型超参数的有效性和性能，选取随机超参数模型、网格搜索法和参数随机优化3个模型进行诊断结果对照，分别命名为Model1、Mod-el2和Model3。各模型中超参数集如表2所示。此外，各模型训练过程中的迭代次数均设置为200次，且缺陷识别结果取10次运行结果的均值作为最终识别精度。

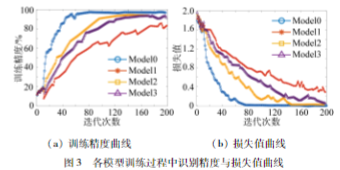
　　所提模型在优选参数下与3个对比模型的训练精度曲线如图3(a)所示，损失值曲线如图3(b)所示。可以看到，所提模型的收敛速度更快，且在收敛后曲线波动幅度最小。

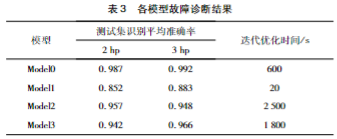
　　各模型在不同负载条件下的故障缺陷诊断结果和各模型迭代优化（运行）时间如表3所示。可以看到，所提模型Model0相较于各对比模型在识别准确率方面具有显著优势，在负载2hp和3hp条件下的平均准确率分别为98.7%和99.2%,相较于随机超参数模型，识别准确率提升了15.85%和12.34%。此外，对比各模型迭代优化时间，可以看到固定参数后的单一训练时长仅20 s,一方面得益于数据量较小，另外则说明所提特征优选结合深度长短时网络模型的故障诊断框架具有较高的特征提取效率和缺陷识别精度。相较于网格搜索和随机优化，贝叶斯优化超参数模型获得了更高的识别精度的同时，具备更短的迭代优化时间，即所提方法能够在实现更高识别精度的同时兼顾训练效率。

　　4结束语

　　为实现更高效率和更高的轮对轴箱缺陷识别精度，本文提出基于贝叶斯优化的全模型超参数优化架构，框架基于VMD时序信号预处理、多尺度散布熵特征提取、MCMR特征集合优选以及深层LSTM模型中对缺陷识别影响较大的超参数集实现振动信号数据驱动的缺陷诊断模型，针对各功能模型种典型超参数，采用贝叶斯优化实现全模型参数协同优化。研究基于CWRU公开数据集中不同负载下的缺陷数据验证了所提诊断模型的有效性。

　　对比了3种不同超参数优选诊断模型，即随机超参数模型、网格搜索优化模型和参数随机优化模型，实验结果表明基于贝叶斯优化的模型在训练效率和训练收敛性等方面具有显著优势，较其他模型最多提前60迭代次数完成收敛，识别精确度较随机超参数模型提升了15.85%。表明所提模型在实现更高识别精度的同时具备更高效的寻优策略。因此，该模型具备应用于HXD1D型电力机车轴箱轴承故障的技术基础。

　　[1]人民日报海外版．“一带一路”交通互联互通迈上新台阶[EB/OL]//[2024-02-23].

　　[2]王冲．人工智能将提高未来铁路信号的安全性和效率[J].铁路通信信号工程技术，2024,21(8):115.

　　[3]LUO H,BO L,PENG C,et al.Fault Diagnosis for High-SpeedTrain Axle-Box Bearing Using Simplified Shallow Information Fusion Convolutional Neural Network[J].Sensors,2020,20(17):4930.

　　[4]张又才，朱伏平．基于全矢CEEMDAN滚动轴承故障诊断研究[J].机械设计，2023,40(S2):68-72.

　　[5]郭凯，马军，熊新，等．改进VMD及补偿距离的滚动轴承故障检测方法[J].控制理论与应用，2024(2):1-9.

　　[6]王发令，吴佳敏，陈冠雄．基于小波包奇异谱熵和IWOA-ELM的列车轴承故障诊断[J].机电工程技术，2023,52(5):295-299.

　　[7]张韦，张永，骈晓琴，等．基于改进EMD样本熵和SVM的风机滚动轴承故障诊断[J].机电工程技术，2021,50(12):38-41.

　　[8]谢平波．基于EEMD和HT的三相异步电机断相故障检测研究[J].机电工程技术，2014,43(6):66-69.

　　[9]杜文辽，高军杰，杨凌凯，等．多尺度加权CEEMD-1DCNN旋转机械故障诊断[J].机床与液压，2023,51(17):202-208.

　　[10]郑近德，苏缪涎，潘海洋，等．自适应噪声加权优选经验模态分解及其在机械故障诊断中的应用[J].振动工程学报，2021,34(4):869-878.

　　[11]岑潮宇，代亮成，池茂儒，等．基于精细复合多尺度散布熵的抗蛇行减振器故障诊断[J].铁道科学与工程学报，2024(10):4334-4343.

　　[12]郑近德，姚殷柔，潘海洋，等．多尺度熵方法在机械故障诊断中的应用研究进展[J].安徽工业大学学报（自然科学版），2024,41(1):46-57.

　　[13]周玉，房倩，裴泽宣，等．基于改进麻雀搜索算法优化LSTM的滚动轴承故障诊断[J].工程科学与技术，2024(2):289-298.

　　[14]何凯，廖玉松，张小光．基于N GO-VMD和D BO-SVM的滚动轴承早期故障诊断[J].西安航空学院学报，2024,42(1):41-47.

　　[15]吴亚丽，冯梦琦，王君虎，等．变分模态分解和自适应稀疏自编码器的故障诊断模型[J].机械科学与技术，2023(12):1-8.

　　[16]陆志杰，王志良，鄢小安，等．变分模态分解方法在轴承故障诊断中的应用研究进展[J].润滑与密封，2024(9):178-190.

　　[17]李顺勇，王改变．一种新的最大相关最小冗余特征选择算法[J].智能系统学报，2021,16(4):649-661.

　　[18]张宏杰，陈贵凤，闫宏伟，等．基于SMOTE与B ayes优化的LSTM网络变压器故障诊断[J].中国电力，2023,56(10):164-170.

　　[19]贾皓阳，钱宇．基于贝叶斯优化XGBoost算法的变压器故障诊断[J].黄河水利职业技术学院学报，2023,35(2):37-43.

　　[20]董丽娟，方召，陈会涛．基于深度学习和贝叶斯优化的压缩机故障诊断[J].机械设计与制造，2023(2):45-52.

　　[21]王一博.HXD1C型电力机车牵引齿轮故障诊断[D].兰州：兰州交通大学，2020.

　　[22]张文博.HX__D1C型电力机车轴箱轴承故障诊断方法研究[D].兰州：兰州交通大学，2024.