摘要：在进行结构设计时通常会对结构进行模型简化再计算。简化合理则计算结果与实际情况相符。但在某些情况下，简单的简化与实际情况却有明显区别。分析了一个海盗船游乐设施的吊杆实例。当杆摆到最高点接近水平状态时，若按静止梁结构来计算，则其自重产生的弯矩将很大。然而由于其随船体自由摆动，并不能这样来简单计算。直观上，它像是一根自由摆动的受拉刚性杆，并不会承受弯矩。按上述不同的简化模型对吊杆的设计产生很大的影响。通过结合机构的运动特性及结构特点，逐层分析并建立符合其动力学特征的受力模型，并结合整体受力分析及局部结构之间的相互作用和内力传递情况，分析出一种更贴近其真实受力情况的计算方法，从而得出吊杆的实际受力，为吊杆的型材截面、材质等方面的选择提供可靠的依据。从而使结构更安全和更具合理性。
      关键词：摆动；吊杆；自重；动态受力

　　0引言

　　游乐设备在国外已有100多年的发展历史，而我国的游乐设施起源于20世纪80年代，起步相对较晚，各方面相对不完善[1-2]。游乐设备事故时有发生[3-4]。

　　海盗船（图1)属于观览车类的摆锤型游乐设施[5-7],对于海盗船形式的结构，其主要结构特点：采用一根主梁作为船体的主支撑，主梁两端安装斜吊杆，两个斜吊杆汇聚到吊点位置，形成吊挂结构。

　　运行时，通过驱动轮对船梁底部进行摩擦驱动，使船体开始往复摆动，并且在逐次摆动中累积能量，最终船体越荡越高，速度也越来越快。驱动轮只在底部区域作用，当船体荡起来后，将在惯性和重力的作用下自由摆动。

　　摆锤型游乐设施主要有大摆锤、海盗船两种典型产品。刘海生等[8]对摆锤的三维设计做了研究，马栋联等[9]基于SolidWorks对大摆锤机身做了有限元分析，卢镇海等[10]对大摆锤的吊臂进行了研究，薛真等[11]对含裂纹的摆锤减速器行星齿轮做了疲劳寿命分析，陈朝阳等[12]对摆锤的加速度做了分析，而关于海盗船的研究相对较少。

　　按通常的理论设计及计算方式[13-14],设计者会对结构进行模型简化后再进行计算。不过简化模型考虑不全面时会对结果产生明显影响。下面对一个看似简单的海盗船吊杆摆动过程受力问题进行分析，先从容易理解的方式进行考虑，再逐次深入分析影响其受力的各种因素，从而得出不同因素对真实受力的影响。

　　通过分析可以发现，船体整体自由摆动时，吊臂并不自由，而是受到整体结构的约束，并通过连接结构传递相互作用力。当吊臂摆到最高处时，将不只是承受拉力，还会受到自重以及整体运动角加速度综合作用而产生的弯矩。受弯与纯受拉对结构的设计要求不同，所以只有全面考虑才能确保设备真正的满足设计要求。

　　1静态常规受力分析

　　简单考虑时，海盗船类似于一个荡秋千的受力形式，对其吊杆进行受力分析时，可以简化为图2所示模型。

　　如图2所示，船体在摆动，忽略吊杆自重，由力的平行四边形分解合成方法，即可算得单根吊杆的拉力为：

　　式中：G船为船体所受重力；F船为离心力。

　　对于荡秋千的吊绳计算，由于吊绳是柔软的，外载荷对其作用最终都会形成拉力，而不会形成弯矩，而它的自重与其本身的抗拉能力相比，其影响几乎可以忽略不计，因而采用上述方法所算得的受力预期实际受力是符合的。

　　但对于海盗船，其体量比秋千大得多，其吊杆的跨度也会大很多。其次，海盗船的吊杆不光要承受前后摆动过程中的拉力作用，还要兼顾限制侧面方向的摆动。同时又要确保足够高的安全系数。因此，吊杆不能简单地只采用绳索。通常的做法是用钢管做成四根吊杆，前后方向各两根，而同一边的两根钢管再用横管连接成一片平面桁架结构。

　　以上计算分析船的载荷对吊杆产生的应力情况，但没有考虑吊杆自重的影响。由于吊杆是一个刚性较强的型材，而不是柔软的绳索，而且跨度较大。因而有必要对吊杆自重的影响进行分析。

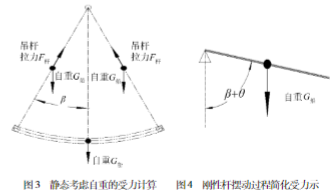
　　图3所示为静止状态下吊杆的受力示意。静止状态时没有离心力，吊杆所受的拉力由船体的拉力和自身重力的拉力方向分量组成，所有此时单根吊杆的拉力为：

　　式中：G船为船自重；G杆为吊杆自重；α为静止状态时吊杆的倾斜角；L吊杆两端铰接长度；为F杆为单根吊杆所受的拉力；M杆为单根吊杆由于自重而受到的最大弯矩。

　　由于吊杆是倾斜的，则吊杆自重在垂直吊杆方向的分量会以均布力的形式加载在吊杆上。吊杆两端按铰接计算，按照简支梁均布载荷的公式，可得吊杆在自重作用下产生的最大弯矩为：

　　可得静态情况下吊杆承受弯矩，不过由于此时角度很小，故对结构选型的影响不大。而大角度摆动时，最高处的吊杆按何种方式受力，则影响很大。

　　2动态受力分析

　　上述研究的是静止状态下，自重对吊杆的附加应力情况。由于静止时吊杆的倾斜角较小。而由于设备是可以摆动的，摆动过程的吊杆的最大倾斜角会比静止时大很多。

　　摆动过程的受力如图4所示，其中θ为摆动角度，ω为瞬时摆动角速度，L为船体质心转动半径，吊杆的质心转动半径为0.5 L,v为船体质心的瞬时线速度，m船为船体的质量，m杆为单根吊杆的质量。船体开始摆动时船底受到驱动轮的摩擦驱动，当船体摆角增大后船体与驱动轮脱离接触，船体变成自由摆动。下面的分析针对大摆角的阶段来展开，故船体按自由摆动来分析为方便理解，因此分两步来逐步探讨吊杆的受力情况。(1)单独的一根刚性吊杆在摆动时的运动受力分析，以明确刚性杆需要多考虑的内容。(2)船体与吊杆组合成一体后的运动受力分析。

　　2.1刚性吊杆摆动时

　　单独取出最上面的吊杆，并简化为刚性杆模型。由于拉力对杆的影响很小，所以下面的计算只讨论弯矩的问题，拉力则不进行计算探讨。细杆由于具有刚性和均布质量两种特性，它的摆动作用力由自重和支点约束力共同提供。而由于杆的刚性特性，杆上各个质点都不再是单纯的各自绕支点自由摆动，而是相邻质点之间会由于相互的牵扯而相互影响，最终形成整体摆动的运动效果。由于杆上各质点所处的位置的不一样，所以它们除了拥有相同的角速度和角加速度外，其圆周线速度以及切向加速度都不一样，由此相邻质点之间会产生切向作用力，由此为弯矩的产生埋下伏笔。

　　根据分析研究，其受力情况其实可以用转动惯量作为切入点来计算说明。刚性杆相对于转动点的转动惯量为：

　　杆的旋转驱动力为自重，综合作用在中间位置。摆动驱动力矩为：

　　因为吊杆是刚性的，所以它上面所有质点的瞬时角加速度相同。算得吊杆的瞬时角加速度：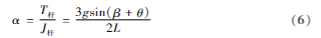

　　则吊杆上距离端点O的距离为x的质点的切向线加速度a1=αx。(x为杆上任意某位置的点距离支点O的距离，其取值范围为0~-L。）对于杆上的质点，它的运动由自身重力和相邻质点的传递的内力共同决定。其中，重力产生的切向加速度分量为gsin(β+θ)。

　　杆上各个质点受到的综合切向加速度分量公式为：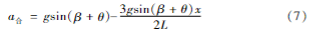

　　其中，此加速度考虑了重力加速度和惯性力等因素，它对应杆上的作用力分布，而非单纯的运动加速度。

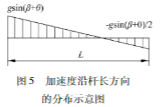
　　综合切向加速度分量沿吊杆的长度方向分布如图5所示。加速度与作用力成正比关系，乘以单位长度质量Δm=m杆/L,即代表作用力的分布。因而最上面的吊杆所受侧向载荷分布情况可以得出。

　　2.2船体与吊杆组合整体分析

　　从2.1节对吊杆的分析可以看出，由于吊杆上各质点与转动圆心的距离不同，相互之间为了运动的协调而产生了相互作用力，从而产生了横向弯矩。

　　当考虑船体与吊杆组合整体结构时，情况还会更复杂一些。此时吊杆的运动不光会叠加船体的影响，同时还需叠加另一侧的吊杆的影响。沿用上面计算刚性杆的思路，还是通过先计算整体的运动情况，得出整体运动的角加速度。再算出吊杆上的加速度分布，从而得到吊杆的受力分布，分离出重力分量后，便可以得出杆内力的分布情况，从而可以得出吊杆内部的弯矩情况。如图6所示。

　　单个吊杆相对点O转动时的转动惯量为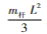J其中吊杆质心转动半径为L/2,吊杆质量为m杆。船体按圆弧刚性杆进行简化，则其相对点O转动时的转动惯量为：

　　J船=m船L(8)

　　式中：船体质心转动半径为L船；船体质量为m船，船体和两根吊杆组成一个整体来计算，总质量m=m船+2m杆。

　　由于两个吊杆对称，所以船体和两根吊杆组成一个整体总质心仍然在中轴线上，算得总质心的转动半径为：

　　整体绕转轴的转动惯量为：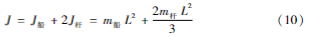

　　摆动驱动力矩：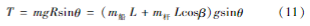

　　从而算得总体的转动角加速度为：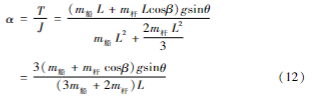

　　重力产生的切向加速度分量为gsin(β+θ)。

　　因此，杆上距离支点x的质点受到的综合切向加速度分量公式为：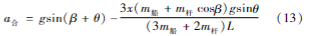

　　吊杆单位长度质量Δm=m杆/L,相应的杆上的作用力分布公式为：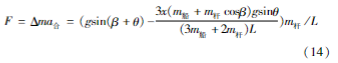

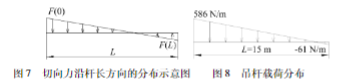
　　由此可以得到吊杆在切向方向上的内力分布，如图7所示。

　　当x=0时，

　　F(0)=gsin(β+θ)(15)

　　当x=L时，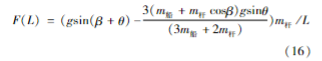

　　即在支点附近，重力分量以力的形式作用在杆上，随着距离支点越来越远，重力分量逐渐变为用于加速。直到有一点，重力分量完全用于加速，这个质点相当于拴在绳子上的小球在自由摆动，不会对杆产生额外的切向力。过了这一点后，质点的加速度超过了重力分量所能提供的，因而是杆的内力与重力一起使之加速，根据力的相互作用原理，该质点也对杆产生了反作用力，力的方向与运动方向相反。切向内力最终会形成吊杆的弯矩。因为有弯矩的存在，因而设计时不能只考虑吊杆抗拉截面的大小，还需要考虑吊臂的截面积与截面系数的关系，因为截面积对应自重载荷，截面系数对应抗弯能力。只有合适的形状比例，才能确保吊杆设计真正的满足设备使用要求。如图7所示。

　　3算例

　　某海盗船的吊杆长度为L=15 m,船体的满载重量为m船=10 000 kg,单边吊杆的质量m杆=900 kg,g=9.8 m/s2,吊杆的安装倾角为β=25°,单边最大摆角为θ=60°。

　　按上述的计算公式，代入数值，可得吊杆上由重力及与船体整体摆动综合作用形成的作用力（考虑运动加速度后剩余的需要结构承受的载荷）分布规律为：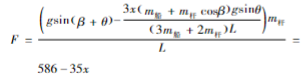

　　即在位于摆动转轴处的杆头位置，F(0)=586 N/m。而在杆尾与船体连接的位置，F(15)=-61 N/m。吊杆切向载荷分布如图8所示。吊杆的切向载荷分布与机械设计手册第1卷第1篇所列举的简支梁渐变载荷模型[15]非常接近，如图9所示。可按该模型进行近似简化计算，按照机械设计手册的计算公式，杆上的最大弯矩为：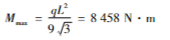

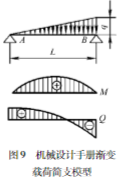
　　吊杆由两根规格为160×80×6的矩管左右并列拼接而成，单个矩管长边的抗弯截面系数为WX=104 cm3,短边的抗弯截面系数为WY=76 cm3。

　　按采用矩管长边抗弯来设计吊杆，则最大弯曲应力为：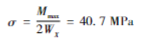

　　由上述计算可知，摆动过程的动态弯矩相对于型材的承载能力而言影响还是相对明显的。假如不注意考虑此弯矩，即使还是这种矩管作为吊杆，但是转90°摆放，由于短边的抗弯截面系数WY=76 cm3,则此时的最大弯曲应力马上增大为55.7 MPa。

　　假如还是采用这样大的抗拉截面积，而其形状变为抗弯截面系数更小的截面，虽然其抗拉承载能力不变，然而弯曲应力却越来越大了。因此，必须考虑动态摆动过程中弯矩的影响，才能全面评估出结构所需的型材截面要求，从而确保结构的安全可靠。

　　4结束语

　　经过分析，看似简单的自由摆杆，在与结构保持整体运动协调的情况下，其受力形式并不同于自由摆动，而是与整体摆动架相互协调并产生相互作用力。此种结构的计算方法，可采用先考虑整体构件的转动角速度和角加速度，从而间接获得结构上各个质点的运动加速度数据。再结合已知的外部受力数据，便可得出结构的内力情况，从而判断结构是否合理。目前很多的设计计算都采用仿真、有限元等方式进行，不过这些方法都有一个前提，就是计算者必须设定正确的力学模型和参数。

　　而模型与参数的设定与计算者对结构的理解也是息息相关的。通过对典型结构的理论受力分析，能更好地把握结构的合理性、准确性、可靠性，从而确保结构的安全。

　　[1]沈勇，鄂立军．国内外游乐设施法规标准比较研究[J].中国安全科学学报，2010,20(11):82-90.

　　[2]顾梅英，游乐设施行业的现状及发展[J].起重运输机械.2009(2):12-13.

　　[3]王丽，富阳．历年游乐设施事故分析研究[J].中国设备工程，2021(5):255-256.

　　[4]郭俊杰，崔明亮，赵强．近十年我国大型游乐设施事故统计分析与对策研究[J].中国特种设备安全，2024,40(2):93-98.[5]TSG 71—2023,大型游乐设施安全技术规程[S].

　　[6]GB?T 18164—2020,观览车类游乐设施通用技术条件[S].

　　[7]GB8408—2018,大型游乐设施规范[S].

　　[8]刘海生，王会刚，董英楠．基于ANSYS游乐设备大摆锤三维设计[J].机械制造与设计，2010(6):45-46.

　　[9]马栋联，李晨阳．游乐设备大摆锤机身有限元分析[J].轻工科技，2017,33(11):52-53.

　　[10]卢镇海，车江龙．摆锤摆臂受力分析[J].机电工程技术，2021,50(8):260-263.

　　[11]薛真，项辉宇，冷崇杰．含裂纹大摆锤减速器行星齿轮的疲劳寿命分析[J].机械传动，2017,41(9):144-149.

　　[12]陈朝阳，王跃勇，李炳坚．大摆锤游艺机加速度分析[J].机电工程技术，2011,40(8):103-105.

　　[13]哈尔滨工业大学理论力学教研室．理论力学(I)[M].7版.北京：高等教育出版社.

　　[14]同济大学数学系．高等数学(Ⅰ)[M].6版．高等教育出版社.

　　[15]成大先．机械设计手册[M].5版．北京：化学工业出版社，2010.