摘要：为深入了解四轮驱动式移动式增氧机的不同状态下的xx特性，针对当前经验公式计算所得的四个明轮推力偏大，对控制系统设计不利的问题，提出了一种基于MATLAB Simulink的仿真方法，用以模拟移动增氧机的xx过程。建立了xx过程的数字仿真模型，仿真分析了移动式增氧机前进和原地增氧模式。结果表明：仿真模拟结果与实际xx特性相符。在前进模式下，移动式增氧机能够实现直线前进；在原地增氧模式下，可以实现原地静止。充分验证了所提数学模型的准确性，对移动式增氧机xx过程的理论研究和实际应用提供了一定的参考价值。

　　关键词：移动式增氧机；xx模型；Simulink

　　0引言

　　目前，我国的河蟹养殖面积约为6.67×103 km2，养殖产量可达80万t，年产值高达550亿元，河蟹已成为我国水产行业的主力之一。在水产养殖过程中，溶解氧浓度是决定河蟹存活率的关键因素之一，其浓度直接影响水产生物的生命力。因此，提高溶解氧浓度被认为是优化水产养殖环境的重要手段。当前应用于水产养殖的增氧机有水车式、叶轮式、射流式、微孔式等款式。然而，这些增氧机通常采用单点增氧方式，其增氧范围有限，可能导致在增氧机固定点处溶解氧过量，而在远离增氧机的地方溶解氧不足。这种增氧方式不仅未能实现理想的养殖效果，还导致了电力资源和人力资源的严重浪费[7]。为解决这一问题，出现了各种形式的移动式增氧机。

　　基于上述研究现状，本文针对无人导航明轮船进行改进。通过运用几何学、牛顿定律以及水动力学原理，提出了一种明轮驱动力计算方法。改进的增氧机不仅能够在固定点实现定点增氧，还能够围绕池塘进行自由移动。为了充分利用明轮船的工作特点，构建了移动式增氧机的xx方程和控制方程，并通过仿真验证了其有效性。

　　首先着重研究了明轮驱动力的计算方法。在此过程中，充分考虑了水动力学原理和几何学的关系，确保了计算结果的准确性。通过这一计算方法，能够更精确地控制明轮船的xx，使其在养殖池中实现精准的增氧操作。这一方面有助于避免在增氧机固定点出现溶解氧过量的问题，同时也能够在需要的地方及时提供足够的溶解氧。

　　其次，基于明轮船的xx特点构建了移动式增氧机的xx方程和控制方程。这一步骤是为了确保增氧机能够在池塘中实现自由而又有序的移动。通过对xx方程和控制方程的建模，能够更好地理解明轮船在不同条件下的运动规律，并进一步优化控制策略，提高增氧机的xx效率。

　　最后进行了仿真验证，以确保所提出的移动式增氧机在实际应用中的可行性和有效性。通过对各种情景的模拟，验证了增氧机的xx稳定性、溶解氧均匀性以及对养殖环境的整体改善效果。仿真结果表明，本文提出的改进方案能够显著提高养殖效果，减少能源和人力资源的浪费，为水产养殖行业的可持续发展提供了一种创新的解决方案。

　　1结构及工作原理

　　1.1结构

　　移动式增氧机是一种给蟹塘、鱼塘、虾塘等水域进行增氧的设备，通过电机驱动叶片的xx，将空气压入水中，实现增氧，提高水产生物的存活率。移动式增氧机可以提高水中的溶解氧的浓度，改善水域，实现蟹塘、鱼塘、虾塘等水域供氧需求，提高水产养殖经济效益。移动式增氧机本体主要包括：主控箱（用于存放主控板、电池等）、工作台（用于固定GPS箱）、船体（2个）、明轮（4个，船体左、右各2个）、船体连接固定板（1个）、驱动电动机（左、右各2个）、GPS定位设备等，如图1所示。其他设备还包括无线通信设备、GPRS、地磁传感器等。

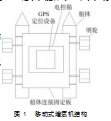
　　移动式增氧机依靠4个明轮实现xx以及增氧。采用机械方法增氧，通过电动机带动4个明轮转动，进而带动水面流动，搅拌气膜和液膜，增加气体、液体的接触面积，以扩大氧气在水中的浓度梯度，提升空气中的氧气向水中转移扩散的速度。

　　1.2工作原理

　　移动式增氧机增氧靠两侧的电机驱动明轮进行增氧，当电机驱动4个明轮同时向前或向后转动时，移动式增氧机将实现向前或向后xx的模式。当前后两对明轮反向xx时，移动式增氧机可以实现原地增氧的模式。

　　移动式增氧机通过GPS定位设备采集移动式增氧机的实时位置信息，通过设备箱内的蓝牙传送到主控箱内的ARM控制板。通过Keil5编写的单片机程序驱动移动式增氧机的电机，通过GPRS与安卓APP进行互连，这样，用户可以通过APP对移动式增氧机进行远程控制。移动式增氧机采用单点增氧与遍历式增氧结合的方式，将溶解氧浓度高的水推向溶解氧低的地方，对池塘全方位进行增氧。

　　2明轮作用力分析与计算

　　移动式增氧机实现全池塘全水域增氧的关键是两侧的明轮，因此在计算明轮作用力的时候，驱动力的计算是至关重要的。

　　2.1明轮机构

　　经过市场调查与实地勘察，发现在增氧机的两侧增氧叶片主要有2种型号，且大多为塑料材质。桨叶数量分别有6片和8片两种。明轮由转动轴和桨叶组成，划水靠桨叶。明轮的结构如图2所示。本文采用6片桨叶的明轮。

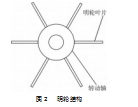
　　2.2明轮驱动力计算

　　电机的正反转xx，带动明轮转动提供驱动力。根据牛顿力学定律可知，当移动式增氧机两侧的明轮作用在水上时，可以对明轮的作用力进行正交分解，此时的驱动力可以分解为水平方向以及竖直方向上的两个力。水平方向上的力可以推动移动式增氧机前进；垂直方向上的力可以抬升移动式增氧机。

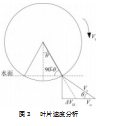
　　根据牛顿第二定律F=ma，其中a为被驱动水体速度的单位变化量即加速度，m为被驱动水体的质量，移动式增氧机的加速度a受到多方面的影响，可计为速度的变化量。单个桨叶明轮推动力Td的计算式为：

　　Td=ma=mΔVH（1）

　　根据图3叶片速度分析并结合几何原理有：

　　ΔVH=Vt sin(90°-θ)-Vo（2）

　　式中：θ为叶片浸没深度角。

　　根据圆周定律，叶片边缘速度Vt为：

　　Vt=πnD（3）

　　式中：n为明轮转速；

　　D为明轮叶片直径。

　　关于m的计算，根据水动力学推导得到：

　　m=ρπ（4）

　　式中：c为叶片入水深度；s为叶片宽度；ρ为水密度。

　　因此，得到总推力的计算公式为：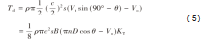

　　式中：B为单个明轮叶片数。

　　3移动式增氧机动力模型的建立

　　移动式增氧机xx特性的分析，必须建立移动式增氧机xx过程的数字仿真模型。该数学仿真模型可以将明轮的作用力转换为船舶的x、y轴方向上的水动力。

　　3.1简化模型

　　为了便于移动式增氧机xx坐标系统仿真分析，模型假设如下：

　　（1）在移动式增氧机前进以及原地增氧两种模式不受风阻力、水阻力的影响，忽略外力对移动式增氧机位姿的干扰，此时移动式增氧机处于理想状态；

　　（2）假设移动式增氧机自带的4个电动机的扭矩以及作用力大小相等，4个明轮上的驱动力大小相等[19]。

　　3.2移动式增氧机的数学模型

　　数学模型是根据Fossen总结的普通舵控方向、螺旋桨驱动船舶的非线性、四自由度数学模型进行改进[20]，将船舶沿x、y轴方向上的水动力X、Y以及绕x、z轴的转矩改变为：

　　■|∂X'=Xu'u u'2+(1-tt)T'(J)TT'+

　　|Y'=''3++Y''2'p''vrϕ'2'''ϕ+'+

　　|Yv'ϕϕv'ϕ'2+Yrϕr'2ϕ'+Yrϕr'ϕ'2

　　|Krr'3+Krvv'r v'2r'Kvr'r v'r'2+Kvv''2ϕ'+

　　|Kv'ϕϕv'ϕ'2+Yrϕr'2ϕ'+Yrϕr'ϕ'2+KL'

　　|Nrr r'3+Nvv'r v'2r'+Nvr'r v'r'2+Nvv'ϕv'ϕ'2+

　　|l Nv'ϕϕv'ϕ'2+Nrϕr'2ϕ'+Nr'ϕϕr'ϕ'2+N'

　　式中：X'、Y'为船舶沿x、y轴方向的水动力；K'、N'为绕x、z轴的转矩。

　　4仿真及结果分析

　　4.1仿真方案

　　移动式增氧机的控制结构如图4所示。通过GPS测量获取当前位置数据，并将其输入到控制器中。在控制器中，通过评估当前点与目标点之间的距离，同时输入移动式增氧机的目标航向和航速信息，进行运算生成明轮的相应控制信号。这些控制信号分别传递给4个独立的控制器，以独立控制每个电动机的转速。

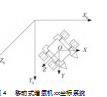
　　为了更精准地模拟移动式增氧机的xx行为，根据其参数计算各水动力系数，进行无因次化处理，并将其代入移动式增氧机的数学模型。在MATLAB软件中进行计算机仿真，以得出系统的行为和性能。仿真模型的详细结构和参数如图5所示。通过仿真能够更好地理解移动式增氧机在不同工作条件下的动态响应和性能特性，为系统的优化提供科学依据。

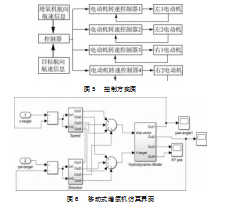
　　4.2前进xx仿真

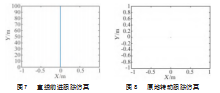
　　从图7中可以发现，当保持移动式增氧机两侧明轮转速一致的时候，两侧明轮推力相等，在无外力干扰条件下，移动式增氧机保持直线航行。

　　4.3原地增氧xx仿真

　　从图8中可以发现，当移动式增氧机两侧明轮按照前两轮正转后两轮反转，在无外力干扰条件下，移动式增氧机保持在原地保持不动。

　　5结束语

　　本文提出一种基于MATLAB Simulink的仿真方法，用于模拟移动增氧机的xx过程。改进了Fossen总结的普通舵控方向和螺旋桨驱动船舶的非线性四自由度数学模型，以更准确地描述和分析移动增氧机的xx行为。通过建立数字仿真模型并给出相应的计算表达式，深入理解移动增氧机的xx特性，为系统设计和性能优化提供有力工具和方法。首先，通过改进Fossen的数学模型，使其更适应移动增氧机的特殊xx情境。考虑到移动增氧机的工作原理和特点，对船舶的非线性四自由度数学模型进行了细致调整。这一改进不仅提高了模型的适用性，也使得仿真结果更具可信度。其次，采用MATLAB Simulink仿真工具建立了移动增氧机的数字仿真模型。使用改进后的数学模型和相应的计算表达式，准确地模

       参考文献：

　　[1]朱寅.超声变幅杆有限元谐振分析[J].机械,2005(12):13-15.

　　[2]陈硕.基于ABAQUS超声振动钻削系统变幅杆模态分析[J].精密制造与自动化,2018(2):19-21.

　　[3]王忠进,缪兴华,胡神阳,等.基于有限元方法的阶梯形超声变幅杆的设计与修正[J].电加工与模具,2018(1):61-xx.

　　[4]洪波.基于Solidworks的机床横梁有限元模态分析[J].职业,2013(5):88.

　　[5]伍利群.变幅杆外形结构对超声纵向振动性能参数的影响[J].机械设计与制造,2010(4):212-213.

　　[6]许敏,薛惠芳.基于SolidWorks的鼓风机叶轮有限元分析[J].风机技术,2011(4):43-47.

　　[7]李新和,秦清源,何霞辉,等.超声旋压复合变幅杆的设计计算与仿真分析[J].机械科学与技术,2014,33(8):1155-1160.

　　[8]汪锐,王艳.基于Abaqus的超声变幅杆设计及有限元分析[J].农业装备与车辆工程,2021,59(2):127-130.

　　[9]段宇飞.旋转超声冲击表面强化的实验研究[D].太原:太原理工大学,2016.

　　[10]方正,韦相福,陈德灯,等.Z14巴哈赛车系统优化设计研究[J].装备制造技术,2022(9):70-74.

　　[11]王斌,阮立,王燕飞,等.基于有限元方法的电动自行车静动力学仿真[J].自动化仪表,2022,43(1):77-81.

　　[12]吴立敏,文怀兴,隆志力.纵振超声刀柄优化设计研究[J].压电与声光,2019,41(1):85-88.

　　[13]曾亮,沈萌红,钱孝华.ANSYS在超声波电机设计中的应用[J].机电工程,2009,26(3):84-86.

　　[14]陈广鹏,江京亮,赵官传,等.基于Abaqus多频率超声变幅杆稳态及谐响应分析[J].机床与液压,2019,47(11):147-150.

　　[15]刘炜,吴运新.超声换能器ANSYS建模及谐响应分析[J].科学技术与工程,2009,9(10):2728-2731.

　　[16]王家祥,廖金麒,毛奇,等.圆锥形超声变幅杆的设计及实验分析[J].机械工程与自动化,2018(6):18-20.

　　[17]赵明利,程雪利,赵波.带工具头超声变幅杆节点定位偏差问题分析[J].声学技术,2013,32(3):253-256.

　　[18]李乾坤,李学旺,赵春雨,等.机械密封中Ω形和U形波纹管的疲劳寿命分析[J].机电工程技术,2023,52(12):163-166.