摘要：为了满足当今市场对电动摩托车性能要求，设计了一套电动摩托车动力总成控制系统，根据市场调研结果以及考虑到电动摩托车的动力性能，选取一款内嵌式永磁同步电机（IPMSM）作为动力核心，72 V蓄电池组作为动力源，采用矢量控制策略对驱动系统进行动力匹配。为了实现更宽的调速范围，提高电动摩托车的续航里程，提出了一种适用于IPMSM驱动器高速运行的最大转矩电流比（MTPA）弱磁控制算法。基于速度指令，运行模式将自动从恒定转矩区变为弱磁区。为了使电动摩托车在复杂路况下也能平稳行驶，排除系统内部参数扰动对最终控制效果的影响，在矢量控制系统的转速环引入了基于指数趋近率的滑模速度控制器（SMC）。使用MATLAB/Simulink搭建了控制系统仿真模型，并对动态负载工况和稳态负载工况进行仿真，结果表明所提出的控制策略是可行的。最后，搭建了电机控制器动力总成系统测试平台，进行电机和控制器的综合性能测试，结果表明所设计的动力总成系统较市场上同类产品效率提高约5%。

　　关键词：永磁同步电机；弱磁控制；滑膜控制；矢量控制

　　0引言

　　电动摩托车作为一种环保、高效的城市交通工具，在当今社会中备受关注。其推动力的核心元件之一是永磁同步电机（PMSM）。PMSM由于其优越的特性在工业领域被广泛应用。它是由参数时变的高阶复杂动力学组成的非线性系统。在永磁同步电机的闭环控制中，控制算法的研究是一项重要的内容，学者们提出了很多的控制算法用来提高闭环控制系统的性能。

　　当电动摩托车运行时，电机转速的控制效果容易受到外部干扰影响，传统的PI控制器只能够满足一定的控制需求，无法实现对驱动电机的高性能控制。郭栋等[1]

　　提升调速系统转速环的控制效果，采用了改进的滑模控制器（Sliding Mode Control，SMC），但此控制结构只适用表面式永磁同步电机。刘庆华等[2]提出将MTPA与SMC算法相结合，对内置式永磁同步电机进行调速控制。Qu L等[3]提出一种新的基于扩展状态观测器的滑模速度控制方法，对系统内部参数以及外部负载变化具有较强的抗干扰能力。陈德海等[4]为进一步抑制永磁同步电机（PMSM）调速系统控制所产生的不稳定性问题，在传统指数趋近律基础上，设计了一种新型的趋近律。郭小定等[5]提出了一种新型指数趋近律，系统在引入该趋近律后保证状态变量趋近速度与滑模面切换函数相关联，实

　　现趋近速率自适应调节的能力。对于在电压与电流限制下采用弱磁控制算法方面，刘欢等[6]提出一种将MTPA控制和超前角弱磁控制相结合的混合控制策略；章回炫等[7]提出一种基于电流预测的车用永磁同步电机弱磁控制方法，以提升永磁同步电机弱磁区动态性能；金鑫[8]提出一种永磁同步电机交轴电流误差积分反馈深度弱磁控制策略；赵羽[9]研究了不同弱磁控制策略在SVPWM与六步电压法结合的混合调制算法下的性能；并针对调制算法切换瞬间出现转矩波动的问题进行了理论分析，最终确定了适用于混合调制算法的弱磁控制策略。

　　本文引入了一种非线性控制方法也即滑模变结构控制（SMC），SMC不依赖于精确的数学模型，对系统内部参数扰动的敏感度低而且控制精度高。对于IPMSM而言，电流环的控制通常通过MTPA算法进行控制，为了可以得到更宽的调速范围，本文提出了一种将MTPA、超前角弱磁控制以及滑模控制匹配在一起的混合控制策略。弱磁控制算法配合MTPA控制算法可以实现对电机全频率范围下的调速。

　　1永磁同步电机数学模型

　　在同步旋转坐标系下，IPMSM的定子电压方程为：

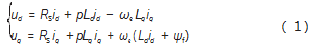
　　IPMSM的电磁转矩方程为：

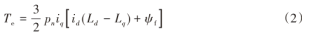
　　PMSM的机械运动方程为：

　　式中：J为转子和系统的转动惯量；Tl为负载转矩；ωr为电机的机械角速度；B为阻尼系数；ud、uq分别为d、q轴的电压；ψd、ψq分别为d、q轴磁链；Ld、Lq分别为d、q轴电感；R s为定子电阻；ωe为转子旋转的电角速度；p为微分算子度。

　　2基于电流超前角IPMSM弱磁控制

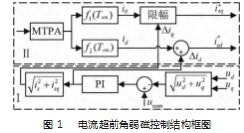
　　电流超前角的弱磁控制策略如图1所示。其中Ⅰ部分表示弱磁判定模块，当电机的转速升高到基速以上时，才可以通过控制电流超前角的大小来对dq轴的电流进行分配，使其可以按照计划的工作轨迹运行。判定依据为，

　　当

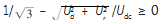
时，此时电机的端电压未达到电压极限圆的最大值，此时电机工作在受MTPA控制的恒转矩区域。

　　第Ⅱ部分即表示电流调节模块，电机转速达到基速时，便进入弱磁控制阶段，判定的依据为

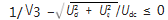
　　表示电机端电压达到了电压极限圆最大值，此时便需要对MTPA模块输出的电流值进行重新分配。取电机逆变器端电压的最大值与电流调节输出电压Ud和Uq的平方和的差值，经过PI调节器来持续输出电流超前角β的值(−π/2~0之间）。其中直轴电流的大小由输出的电流超前角直接确定，交轴电流的大小通过Δq限幅值得到。限幅值模块可以使得电流内环的响应更加迅速，在系统运行过程中可以让电流始终跟随给定电压值变化。iq在弱磁调节环节后进行了重新分配，其中iq在d轴的分量也即|iq|·sinβ与id相互作用，充当了去磁分量。iq作为去磁分量，始终是与原来id的方向相反。iq·cosβ作为弱磁限幅后的iq，使得电机转速在弱磁控制时可以进一步提高。

　　根据电流超前角弱磁控制结构框图可以搭建出弱磁超前角的MATLAB/Simulink仿真模型，如图2所示。

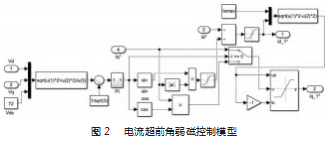
　　3基于指数趋近律的滑模控制器

　　由于滑模控制本身是非线性的控制方法，具有一定的开关特性，使得电机运行过程中产生的反电动势中含有高频谐波，造成系统的抖振，因此滑模控制器就需要采用低通滤波器来消除高频的抖振现象本文采用了基于指数趋近率的滑膜速度控制器。

　　滑模速度控制器主要是对PMSM的转速进行跟踪。定义转速误差：

　　选取PMSM系统的状态变量为：

　　忽略PMSM的阻尼系数，式（3）所示的机械运动方程可以简化为：

　　将式（2）代入到式（6）中整理可得：

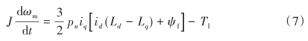
　　得

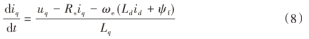
　　根据式（7）~（8）可以得到PMSM的状态方程为：

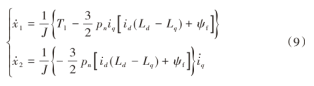
　　定义

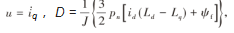
　　则式（10）可以写成：

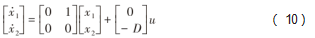
　　定义滑模面切换函数为：

　　式中：c > 0，为待设计参数。

　　对式（11）求导，可得：

　　采用指数趋近率的方法，可得滑模速度控制器的表达式为：

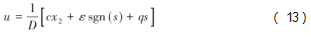
　　式中：ε>0 ，q>0。

　　q轴的转矩电流为：

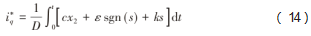
　　根据李雅普诺夫稳定性判据定理，易知：

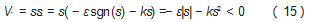
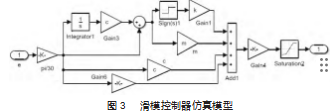
　　因此，该系统符合渐近稳定的条件。建立的滑模速度控制器的Simulink仿真模型如图3所示，其中SMC的参数：c=60，ε=200，q=300。

　　4仿真实验分析

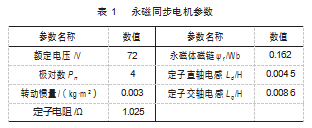
　　为了解决IPMSM在基速下运行时电机转速较低的问题，采用了超前角弱磁控制。为了兼顾电动摩托车的驾驶体验和舒适性，采用了抗干扰能力更强的滑模控制方法。为了验证所提出控制策略的可行性，在MATLAB/Simulink环境下分别搭建了IPMSM最大转矩电流比控制下的仿真模型和IPMSM弱磁控制下的仿真模型。通过改进前后仿真结果进行分析，验证改进后控制策略的可行性。本文采用的为内置式的PMSM，电机的具体参数由电机生产厂家提供，具体参数如表1所示。

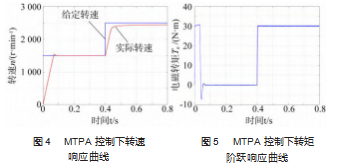
　　如图4所示，为MTPA控制下的转速响应曲线。设定控制系统为空载启动，仿真时间为0.8 s。初始给定转速为1 500 r/min，0.4 s后转速阶跃为2 500 r/min，从图中可以看出，电机大约经过0.1 s后转速稳定在1 500 r/min，稳定后转速的超调量比较小。当0.4 s后转速阶跃为2 500 r/min，此时电机转速又经过0.1 s达到稳态，电机的最大转速约为2 400 r/min，即电机在MTPA控制下，受到电压极限圆和电流极限圆的限制能达到的最大转速为2 400 r/min。如图5所示为MTPA控制下转矩响应曲线，电机空载启动并给定转速为1 500 r/min，在0.4 s时施加负载转矩30 N·m。当电机转速达到1 500 r/min时，会产生一定的超调，此时会用相反方向电磁转矩来调节转速，直到达到平衡状态，图中0.1~0.4 s阶段，此时电机转速稳定在1 500 r/min，无负载转矩。当0.4 s时电机施加了负载转矩，系统也很快做出了反应。

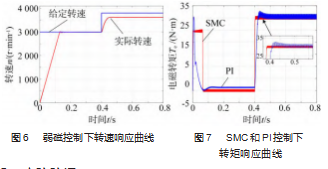
　　为了验证超前角弱磁扩速的效果，弱磁控制仿真模型中电流环和速度环仍保留PI控制器。如图6所示，初始给定转速为3 000 r/min，0.4 s后转速阶跃为3 800 r/min，如图中蓝色线段所示。从图中可以看出，经过0.15 s后电机转速稳定在3 000 r/min，转速的动态响应时间较短，在0.4 s后给定电机转速3 800 r/min，此时电机转速又经过0.05 s达到稳态，电机能达到最大转速约为3 600 r/min，虽然与给定转速之间存在一定误差，但是稳定后转速的超调量比较小。结合前面单独使用MTPA控制的系统，电机的最大转速稳定在2 400 r/min，在超前角弱磁控制下的电机拓宽了最大调速范围，达到了3 600 r/min，仿真结果证明了本文提出的弱磁扩速方案可行。

　　为了验证滑模速度观测器的性能，将PMSM弱磁控制系统仿真模型速度环的PI调节器换成滑模速度控制器，给定初始条件：设定控制系统由空载启动，启动时给定参考转速2 000 r/min，在0.4 s时施加负载转矩30 N·m，仿真时间设定为0.8 s。如图7所示，为IPMSM弱磁控制系统分别在PI控制和滑模控制下电机的转矩响应曲线。从图中可以看出，在0~0.1 s之间，由于电机启动时需要比较大的电磁转矩，因此PI控制和SMC控制下的电磁转矩都迅速上升，并均在0.1 s后恢复到稳定状态。此时两种控制算法的区别并不明显。在0.4 s时由于系统施加了负载转矩，两种控制算法均可以快速响应，其中SMC控制下的转矩的动态性能相较于PI控制时，转矩响应时间更短，超调量更小。局部放大后，可以明显看出系统达到稳定后，在SMC控制下的电机转矩脉动更小。由此可得出结论，在本文所设计的控制系统中，当系统受到外界因素干扰时，滑模控制相较于PI控制鲁棒性更好。仿真结果验证了滑模速度观测器的优越性，达到了预期效果。

　　5实验验证

　　根据磁滞测功系统组成框图搭建的电机控制系统测试平台，被测电机是内嵌式永磁同步电机，电机参数在表1中已经给出。被测电机与控制器进行连接，控制器与72 V锂电池组连接，然后进行电机堵转试验和自动加载试验。

　　5.1堵转试验

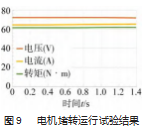
　　如图9所示为电机采用滑模速度控制器和弱磁控制策略进行堵转运行的试验数据绘制的图形，横坐标表示试验时间，纵坐标表示电压、电流和转矩的取值。从图中可知堵转运行时控制器母线电压维持在72 V，电流最高可达到65 A，电机输出的最大转矩为62 N·m。堵转运行时电机的功率达到最大，但是效率为0。

　　5.2自动加载试验

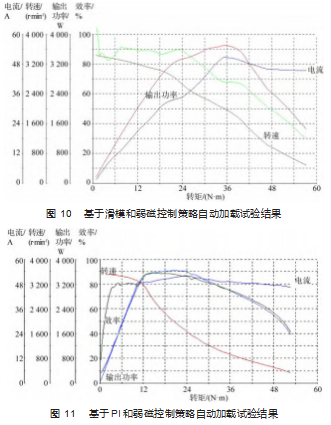
　　测试过程为：设置磁粉制动器按照1（N·m）/s的速度增加，控制器控制电机以最大功率运行，测试控制器在电机负载转矩缓慢增加过程中各参数的变化。如图10~11所示分别为电机采用滑模速度控制器和弱磁控制策略进行自动加载试验结果和PI速度控制器和弱磁控制策略的自动加载试验结果，图像横坐标表示负载转矩，由0 N·m逐渐增大至最大输出转矩60 N·m，分别绘制了电流、转速、输出功率和效率在负载转矩变化过程中的变化曲线。从图中可以看出采用PI速度控制器自动加载试验测得动力总成系统启动时，负载转矩在0~12 N·m阶段效率约为80%，负载转矩在12~24 N·m阶段平均效率约为88%，后随负载转矩增大效率会降低。而采用滑模速度控制器动力总成系统启动时，负载转矩在0~6 N·m阶段效率有所波动，但平均效率可以维持在85%左右，比使用PI控制器高5%，负载转矩在6~24 N·m阶段效率可达90%，6~12 N·m阶段输出效率比使用PI控制器高10%左右，12~24 N·m阶段输出效率比使用PI控制器高3%左右。在负载转矩增加过程中，系统的效率会有所下降。

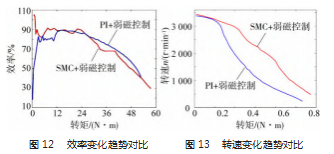
　　为了更好地对比两组试验结果的效率变化趋势和转速变化趋势进行对比，根据试验数据将效率和转速绘制在了同一坐标系中，如图12所示为两组试验效率变化曲线，如图13所示为两组试验转速变化曲线。由图12效率变化趋势对比图可知，当负载转矩在26 N·m范围内变化时，采用滑模和弱磁控制的系统效率更高；由图13转速变化趋势对比图可知，在整个试验过程中，随着负载转矩的增加，采用滑模和弱磁控制的系统转速变化曲线下降更为平缓。根据上述分析结果可知，针对本课题使用的内嵌式永磁同步电机，采用滑模和弱磁控制策略，系统的效率更高，动态性能更好。

　　6结束语

　　本课题主要针对电动摩托车的动力总成控制系统进行研究，基于现阶段电动摩托车动力总成系统发展现状，本文从电机选型、控制策略和控制算法的优化以及控制器设计方案等方面进行了详细研究。研究了IPMSM弱磁扩速原理和滑模控制算法。IPMSM在基速以下时使用MTPA控制，在基速以上时通过弱磁控制进一步提升电机的性能，并通过滑模控制消除电机在温度等外界因素变化时对控制系统产生的扰动。为了验证本文所采用控制策略的可行性，搭建了控制系统MTALAB/Simulink仿真模型。仿真结果表明本文采用控制算法可行。然后搭建了动力总成系统测试平台，进行电机和控制器的综合性能测试，结果表明本文所设计的动力总成系统比市场上的同类产品效率提高5%左右，且动态性能更好。

　　参考文献：

　　[1]郭栋,吴琦,祁晓野.电动汽车永磁同步滑模低速控制[J].电机与控制应用,2017,44(10):119-123.

　　[2]刘庆华,吕永健,阳杰.电动汽车PMSM滑模变结构[J].计算机仿真,2015,12(32):23-132.

　　[3]Qu L,Qiao W,Qu L.An Extended-State-Observer-Based Slid‐ing-Mode Speed Controlfor Permanent-Magnet Synchronous Mo‐tors[J].IEEE Journal of Emerging and SelectedTopics in Power Electronics,2020,PP(99):1-1.

　　[4]陈德海,曹永康,阳攀.基于变指数趋近律的永磁同步电机滑模控制[J].电机与控制应用,2022,49(2):8-13.

　　[5]郭小定,柏达,周少武,等.一种新型趋近律的永磁同步电机滑模控制[J].控制工程,2018,25(10):1865-1870.

　　[6]刘欢.电动汽车用永磁同步电机弱磁控制策略研究[D].武汉:武汉理工大学,2021.

　　[7]章回炫,范涛,宁圃奇,等.车用永磁同步电机高性能弱磁控制策略[J].电源学报,2024,22(2):378-385.

　　[8]金鑫.永磁同步电机弱磁控制策略研究[D].大连:大连交通大学,2018.

　　[9]赵羽.基于混合调制算法的永磁同步电机弱磁控制策略研究[D].哈尔滨:哈尔滨工业大学,2019.

　　[10]Arias A,Ibarra E,Tarancho E,et al.Comprehensive high speed automotive SM-PMSM torque control stability analysis includ‐ing novel control approach[J].Int.J.Electr.Power Energy Syst.2019,109,423-433.

　　[11]王婷婷.基于自适应终端滑模的永磁同步电机调速控制系统研究[D].镇江:江苏大学,2021.

　　[12]孟杰.基于扰动观测器的高性能永磁同步电机电流预测控制研究[D].徐州:中矿业大学,2021.

　　[13]彭鹏峰,许新权,曾洁琼.基于电机效率的纯电动汽车传动系统参数匹配研究[J].机械设计与制造,2021(6):39-44.

　　[14]任金霞,黄艺培,蒋梦倩.PMSM分数阶模型参考自适应调速系统研究[J].河南理工大学学报(自然科学版),2020,39(3):108-113.

　　[15]汤超正,谢卫才,彭磊,等.内置式永磁同步电机MTPA控制效率仿真研究[J].湖南工程学院学报(自然科学版),2022,32(4):6-11.

　　[16]吴尚.永磁同步电机弱磁控制方法与运行效率的研究[D].天津:河北工业大学,2021.

　　[17]Zisui Z,Chenchen W,Minglei Z,et al.Flux-Weakening in PMSM Drives:Analysis of Voltage Angle Control and the Single Current Controller Design[J].IEEE Journal of Emerging and Se‐lected Topics in Power Electronics,2019,7(1):437-445.

　　[18]上海艾瑞市场咨询有限公司.中国两轮电动车智能化白皮书[R]//艾瑞咨询系列研究报告,2021:609-662.

　　[19]赵其进,廖自力,苗成林,等.电传动车辆轮毂电机恒转矩弱磁控制策略[J].浙江大学学报(工学版),2021,55(1):195-202.

　　[20]Sun X,Li Z,Wang X,et al.Technology Development of Electric Vehicles:A Review[J].Energies,2019,13(1):90.