摘要：弓形梁非等高式滑橇起落架前后弓形梁高度不同，无法通过理论分析方法准确获得其着陆性能。为了准确获得其着陆性能，使用仿真分析方法对具有不同着陆速度和壁厚的起落架着陆过程中的重心过载系数和剩余强度系数开展了研究，并结合试验和理论分析验证了结果的准确性。首先，使用动力学方法，开展全机着陆冲击分析，得到了全机重心处着陆过载系数；结果表明，着陆速度较小时，随着着陆速度增加，重心处着陆过载系数几乎呈线性增加；而重心处过载系数随着壁厚增加几乎呈线性增加。随后，基于着陆过载系数，使用静力学分析方法，获得了起落架剩余强度系数，发现起落架壁厚存在最优值。最后，在此基础上，提出了在起落架弓形梁中嵌入内管进行变壁厚设计的方法，相比初始不满足强度要求的设计，该方法大幅提升起落架剩余强度系数至0.2；同时，该方法实现了均匀壁厚起落架不能实现的设计目标，拓展了起落架的设计边界。

　　关键词：滑橇起落架；着陆过载；强度；非线性；优化设计

　　0引言

　　无人驾驶直升机拥有使用灵活、使用成本低的特点，在军事、消防、农林植保和电力巡检等领域具有广泛的应用。在无人直升机系统中，起落架起支撑作用，并在无人直升机着陆过程中吸收能量，保证无人直升机能够平稳着陆。常见的起落架包括滑橇起落架和轮式起落架。由于滑橇起落架结构简单、成本较低，载质量较小的无人直升机通常采用滑橇起落架。

　　根据不同的设计需求，滑橇起落架可以采用不同的布局形式。不同布局形式的起落架，其性能研究通常采用不同的分析方法。对于前后横梁相同且直升机重心位于前后横梁正中间的滑橇起落架，由于结构存在对称性，可以通过梁的弹塑性大变形理论开展着陆载荷分析，理论分析方法能够获得较高的精度。然而，对于前后横梁不同且重心与前后横梁正中间有偏离的滑橇起落架，结构不对称导致滑橇的变形对弓形梁承受的载荷产生影响，使得前后弓形梁分配的载荷无法通过理论方法准确获得，因此，需要采用试验和有限元的方法。

　　有限元仿真分析方法在滑橇起落架性能分析中有较多的应用，许多学者通过与试验对比，验证了该方法在分析滑橇起落架性能中的准确性。吴玉根等通过试验和仿真方法分析了弓形梁为圆形截面的滑橇起落架的着陆响应，使用壳单元模拟滑橇、使用刚体模拟地面，结果表明使用壳单元模拟滑橇的仿真方法可以获得足够的精度，重心下沉位移和着陆过载误差在5%以内。Yildirim等[14]通过试验方法和仿真方法对比了金属滑橇起落架的性能，仿真结果也能和试验结果很好吻合。这些研究表明，使用有限元仿真方法分析滑橇起落架着陆性能是一种有效的方法，具有足够的准确性。

　　因此，本文使用仿真分析方法，对无人直升机用弓形梁非等高式滑橇起落架不同着陆速度下的着陆性能开展研究，并分析了弓形梁壁厚的影响，最后给出了通过改变局部壁厚对起落架性能进行优化、拓展起落架设计边界的方法。

　　1有限元模拟

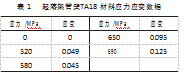
　　某型号无人直升机采用弓形梁非等高式滑橇起落架，起落架通过橡胶垫和抱箍与机体结构进行连接。起落架的前后弓形梁距离地面的高度不同，前弓形梁轴线距离地面的高度为363 mm，后弓形梁距离地面的高度为500 mm；重心与前弓形梁轴线距离在水平面内的投影距离为780 mm，与前弓形梁轴线距离在水平面内的投影距离为620 mm。起落架滑橇和弓形梁管径为40 mm，壁厚为1.5 mm，起落架材料为TA18钛合金，考虑使用的材料强度折减系数为0.9，许用应力[σ]=694 MPa，材料应力应变数据如表1所示。

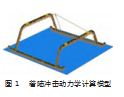
　　本文对起落架性能的模拟使用商用软件Abaqus开展，有限元模型中，使用壳单元S4R模拟起落架滑橇和弓形梁，网格尺寸约为5 mm。起落架与机身连接处的橡胶垫通过非线性弹簧单元进行模拟。忽略机体结构作用，整机质量通过重心处质量点模拟，整机质量550 kg，计算中考虑全机转动惯量。重心质量点通过耦合方式与4个弹簧单元一端连接，弹簧单元另一端通过耦合方式与起落架连接。

　　着陆冲击计算中，根据国军标GJB 720.3A规定，起落架滑橇应与地面保持平行，确保两个滑橇同时触地。如图1所示，地面使用刚体单元模拟，地面和起落架滑橇间的摩擦因数为0.35，由于旋翼产生的升力等于直升机重力，重心质量点和起落架上不施加加速度。根据计算需要，重心质量点和起落架设置合适的初始着陆速度；在刚体单元上施加固支约束。使用显式动力学方法开展计算，计算中考虑几何非线性和材料非线性。

　　着陆强度计算中，根据国军标规定，通常需要考虑四点着陆、侧移着陆、前飞着陆等工况，根据经验，侧移着陆工况通常是起落架的危险工况，因此，本文在研究强度性能时仅考虑侧移着陆工况。根据国军标GJB 720.3A，侧移着陆载荷通过四点着陆获得的重心过载系数计算，该载荷均匀分配在两个滑橇上，在重心处施加固支约束。使用静力分析方法开展计算，计算中考虑几何非线性和材料非线性。

　　2结果与讨论

　　在无人直升机着陆过程中，起落架起到缓冲作用，能够通过吸收着陆冲击能量，降低着陆过程中的最大地面反作用力F地，进而降低机身过载系数。着陆过程中，无人直升机动能和重力势能转化为起落架应变能和地面摩擦热能，由于旋翼升力等于重力，能量平衡方程可以写作：

　　Mv2=∫F地dD（1）

　　式中：D为滑橇相对重心的位移；F地为地面反力。地面垂直载荷为：

　　式中：μ为地面和滑橇之间的摩擦因数。

　　着陆过载系数n=F/(Mg)通常被用来表征起落架的缓冲能力。另一方面，着陆过程中，起落架不能发生破坏，剩余强度系数m表示材料许用应力和起落架中的最大应力的比值，即m=[σ]/σmax，通常被用来表征起落架的安全性。本节将首先研究着陆速度、起落架壁厚对这两个参数的影响，最后讨论如何通过变壁厚设计拓展起落架的设计边界。

　　2.1着陆速度影响

　　图2显示了着陆速度v不同时的着陆过载n。在着陆速度较小时，随着着陆速度的增大，着陆过载系数基本呈线性增加；着陆速度较大时，随着着陆速度增大，着陆过载系数不再呈线性增加。这是由于着陆速度较小时起落架的变形较小，而且起落架中的应力较小，未达到TA18钛合金材料的屈服应力，可以忽略几何非线性和材料非线性影响，式（1）可以写作：

　　式中：k为起落架刚度，忽略非线性影响时为常数。

　　着陆过载系数：

　　根据式（4）可知，着陆过载系数随着着陆速度增加线性增加。而随着着陆速度增加，几何非线性不可忽略，而且起落架中可能出现塑性变形，因此着陆过载系数将出现非线性变化。

　　图3显示了着陆速度v不同时的剩余强度系数m和起落架最大等效应力。在着陆速度v较小时，随着着陆速度v增大，最大等效应力基本线性增加；在着陆速度v较大时，随着着陆速度v增大，最大等效应力不再线性增加。这是由于：着陆速度较小，可以忽略几何非线性和材料非线性影响，重心进行固支约束后，起落架上的最大应力仅与地面反力F地，且随着地面反力F地变化线性变化，由上文可知，地面反力F地随着陆速度v增加线性增加，因此，最大等效应力随着陆速度v增加线性增加。而随着着陆速度增加，几何非线性不可忽略，而且起落架中可能出现塑性变形，着陆过载系数将出现非线性变化。而剩余强度系数m与起落架中的最大应力成反比，因此，会随着陆速度v增加不断下降，并呈现出明显的非线性特征。

　　2.2壁厚影响

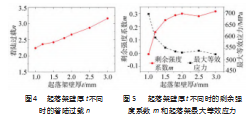
　　图4显示了起落架壁厚t不同时，着陆过载系数n的变化。当着陆过载系数n随着壁厚的变化基本呈现线性变化。这与使用梁模型通过静力学分析方法[10]得到的结果不同。使用梁模型通过静力学方法开展分析时，假设壁厚为t的起落架刚度为k，则k∝t；起落架着陆过程中，根据式（1）能量守恒，考虑到起落架变形不大，忽略变形非线性，着陆速度相同时，地面反力F地∝vt，即着陆过载系数n∝/t。根据Airoldi等[20]的试验和仿真分析结果，即便材料在弹性范围内，滑橇起落架着陆时的地面反力-重心位移曲线仍然具有明显的平台段，在该平台段，随着重心位移的增加，地面垂直反力不断波动，而不会明显增加，这是由于在着陆过程中，冲击波作用使得滑橇和地面间的垂直反力出现明显波动，式（3）中的滑橇刚度k受到冲击影响，不再与壁厚t成正比关系，因此，地面垂向载荷系数n不再与vt成正比关系；而静力学分析方法无法考虑冲击影响，得到的地面反力-重心位移曲线是光滑的曲线，不存在平台段，式（3）中的滑橇刚度k与壁厚t成正比关系，因此，着陆过载系数n∝vt。

　　图5显示了起落架壁厚t不同时，剩余强度系数m以及最大等效应力的变化。在壁厚t=0.1 mm时，起落架最大等效应力均超过694 MPa，起落架发生破坏，剩余强度系数m<0；随着壁厚增加，起落架最大等效应力先是快速下降，在壁厚t>1.8 mm后，缓慢下降，基本保持不变，而剩余强度系数m与起落架中的最大应力成反比，因此，会随起落架壁厚增大不断增加，并最终趋于不变呈现出明显的非线性特征。这表明，在起落架壁厚超过一定厚度后，若要提升起落架的强度，依靠增加壁厚的方式效率非常低；另一方面，考虑到前文所述，着陆过载系数n随着壁厚增加而增大，增加机体结构的着陆载荷，进而增大机体结构的质量，因此，起落架壁厚存在最优值。

　　2.3变壁厚设计方法

　　针对特定的使用条件，起落架需要满足特定要求，因此需要对起落架进行改型。本小节针对同型无人直升机的前后弓形梁各加高100 mm的起落架的性能开展分析，并给出了一种变厚度设计方法，以拓展起落架的设计边界。

　　由于侧移着陆工况下起落架失效位置发生在弓形梁弯曲段，为了提升局部强度，在起落架弯曲段内部嵌入壁厚为0.5 mm的内管（图6黄色段），弯曲段总厚度为2 mm，嵌入的内管长度不同，右侧端面坐标分别为0、3、10和18 cm，如图6所示。

　　图6给出了不同壁厚和不同内管长度起落架着陆过载和侧移工况下的剩余强度系数。对于均匀壁厚的起落架，壁厚t为1.5 mm和2 mm的起落架剩余强度系数均小于0，这意味着起落架等效应力超过材料许用应力，起落架在着陆过程中会发生破坏；同时，根据2.2节壁厚对应力和剩余强度系数的影响分析可知，继续增加壁厚，起落架最大等效应力和剩余强度系数几乎不变，无法通过继续增加壁厚降低起落架中最大等效应力，因此，无法通过改变均匀壁厚起落架的壁厚，获得剩余强度大于0的方案。而对于弓形梁弯曲段嵌入内管的设计，如图6所示，左侧内管右端坐标L=3、10和18 cm时，剩余强度均大于0；另一方面，着陆过载系数小于壁厚为2 mm的均匀壁厚方案，较小的着陆过载系数降低了着陆过程中无人直升机大质量部件对机体的作用力，进而降低了机体应力，提升了全机的低周疲劳寿命。这表明通过在滑橇起落架横梁中嵌入内管进行变壁厚设计，可以拓展起落架的设计边界，实现均匀壁厚起落架不能实现的设计目标。需要注意的是，对于其他壁厚均匀滑橇起落架，即便通过增加壁厚可以获得满足要求的剩余强度系数，采用均匀壁厚的设计也是不利的。另外，图6也显示，随着内管长度的增加，剩余强度系数先增大后减小，左侧内管右端坐标L=3 cm时，剩余强度系数取得最大值0.2，这表明内管长度存在最优值，在进行嵌套内管设计时需要考虑。

　　3结束语

　　本文使用仿真方法对无人直升机弓形梁非等高式滑橇起落架性能开展研究，结合试验结果，分析了着陆速度和起落架壁厚的影响，并提出了一种变壁厚设计方法，得到的主要结论如下。

　　（1）着陆速度较小时，随着着陆速度增加，重心处过载几乎线性增加，起落架剩余强度几乎线性下降；随着着陆速度继续增大，重心处过载出现一定的非线性增大，起落架剩余强度出现一定程度的非线性下降。

　　（2）对于均匀壁厚起落架，起落架壁厚增加时，重心处过载几乎线性增加；而起落架剩余强度系数先快速增加，后缓慢增加，最后几乎保持不变。均匀壁厚起落架的壁厚存在最优值。

　　（3）通过起落架弓形梁弯曲段嵌入内管，可以实现起落架变壁厚设计，实现均匀壁厚起落架不能实现的设计目标，拓展起落架的设计边界。同时，内管长度存在最优值，在进行嵌套内管设计时需要考虑。

　   参考文献：

　　[1]卢艳军,刘宏斌,张晓东.基于ADRC的无人直升机飞行控制系统设计[J].机电工程技术,2023,52(2):154-158.

　　[2]孙盛智,孙小婷,郑卫娟,等.舰载无人直升机作战应用模式及关键技术[J].兵器装备工程学报,2022,43(1):68-72.

　　[3]梅蓉.森林环境下的无人直升机安全飞行控制[J].上海交通大学学报,2020,54(9):994-999.

　　[4]胡聪旭,周建平,刘新德,等.前飞来流和侧风对植保无人机下洗流场影响的数值模拟研究[J].中国农机化学报,2022,43(5):61-70.

　　[5]彭向阳,王柯,肖祥,等.大型无人直升机电力线路智能巡检宽带卫星通信系统[J].高电压技术,2019,45(2):368-376.

　　[6]吴靖,胡国才,刘湘一.滑橇式直升机地面共振机体动力学特性研究[J].振动与冲击,2019,38(21):216-220,264.

　　[7]陈明祥.弹塑性力学[M].北京:科学出版社,2007.

　　[8]段煜,齐瑞.振动输送机橡胶弹簧优化设计[J].轻工机械,2023,41(1):90-96,104.

　　[9]MIKHAILOV S A,KOROTKOV L V,NEDEL'KO D V.Analysis of static loading for a helicopter tubular skid landing gear[J].Russian Aeronautics,2012,55:348-352.

　　[10]魏凯,陈铭.轻型直升机起落架的载荷分析与设计[J].飞机设计,2012,32(2):28-31.

　　[11]何洁,徐平华,袁子舜,等.基于机器学习的UD布弹道冲击有限元结果分析[J].轻工机械,2024,42(4):7-15.

　　[12]邓辉,崔建昆.基于AdvantEdge的7075-T651铝合金铣削参数有限元仿真优化[J].轻工机械,2022,40(4):40-46.

　　[13]吴玉根,毛春见,周忠斌,等.复合材料滑橇式起落架落震性能分析[J].复合材料科学与工程,2021(7):68-75.

　　[14]YILDIRIM O,GÜNAY E,ANILÖ,et al.Analysis of a skid type landing gear of a rotary wing UAV by experimental and numerical methods[J].Acta Physica Polonica A,2015,127(4):1170-1175.

　　[15]中国民用航空总局.中国民用航空规章第25部运输类飞机适航标准:CCAR-25-R3—2001[S].2001.

　　[16]刘大海,陈劲东,李波,等.TA18中强钛合金管数控弯曲成形工艺与结构参数显著性分析[J].锻压技术,2021,46(4):156-165.

　　[17]中国xxx总装备部.军用直升机强度规范第3部分机体结构和系统强度:GJB 720.3A—2012[S].

　　[18]胡松,祖磊,李书欣,等.复合材料无人机滑橇式起落架设计与优化[J].玻璃钢/复合材料,2018(3):26-32.

　　[19]赵知辛,郭强,黄鸣远,等.仿竹设计在无人机起落架结构中的应用[J].机械科学与技术,2021,40(11):1798-1804.

　　[20]AIROLDI A,LANZI L.Design of skid landing gears by means of multibody optimization[J].Journal of Aircraft,2006,43(2):555-563.