摘要：针对应用于高速轻载环境下凸轮设计问题，以特种缝合设备珠边机的仿手工线迹缝合勾线机构工作过程为例，使用SolidWorks建立凸轮滚子机构基本模型，基于从动件运动规律利用反转法求解出从动件滚子中心点的运动轨迹，对比不同廓线的运动规律，生成正弦凸轮廓线，然后基于SolidWorks的Motion分析功能，对凸轮运动参数和实际廓线进行优化，并利用MATLAB对其运动性能进行分析验证；为了进一步提高凸轮的疲劳寿命，通过Workbench的Ncode模块，对凸轮建立动力学模型，建立了关于盘形凸轮的寿命优化模型，采用模拟退火算法对七次多项式曲线的系数进行优化，得到新的廓线模型，用Ncode模块计算其最小寿命提高到原来的14倍左右，验证了所提出的凸轮设计方法的优越性。

　　关键词：凸轮廓线；高速轻载；反转法；运动仿真；MATLAB;疲劳分析

　　0引言

　　凸轮机构结构简单，可以根据不同运动要求设计廓线以控制从动件的运动规律,在机械传动特别是纺织机械中应用广泛。珠边机是纺织机械中能够实现仿手工线迹的特种缝纫设备,在高档服装设计制作中被大量使用，而且一些特种缝合场合需要对珠边机凸轮进行重新设计。

　　本文以珠边机勾线机构凸轮设计为研究对象，该机构以凹槽凸轮滚子传动，勾线杆通过连杆与凸轮滚子连接，形成平面凸轮运动机构。凸轮廓线的形状直接影响滚子的运动特性，较平滑的凸轮阔线有助于减小运动冲击、保持更好的运动特性，但同时要考虑运动性能与加工成本之间的矛盾。本文基于SolidWorks建立凸轮机构基本模型，根据从动件滚子的运动特性需求设计出从动件滚子的运动轨迹，利用反转法使凸轮反转最后得到滚子中心点的运动轨迹，依照轨迹生成凸轮廓线，基于SolidWorks的Motion功能，对凸轮运动参数进行分析，以得到凸轮实际廓线，然后利用MATLAB进行运动性能分析，随后利用Workbench的Ncode模块对凸轮建立动力学模型和寿命优化模型，通过模拟退火算法优化七次多项式廓线的系数，进而改用优化后的七次多项式曲线，得到满足疲劳寿命设计的凸轮廓线。

　　1建模与仿真

　　手工线迹如图1所示，仿手工线迹缝合的珠边机结构大致可以分为针杆机构（包括封针机构、上勾线机构）、下送线机构（包括下送线指、下送线钩）、紧线机构（包括夹线器、紧线钩）、下挑线钩和稳线机构、送料机构（包括上下送料、珠点调节）和下勾线盘机构。其中，本文研究的勾线机构运动简图如图2所示。图中的机构由5个构件组成，且该机构为平面机构。构件2为本文研究的凸轮，3号构件为滚子，安装在凸轮与推杆之间，可以减少凸轮与滚子之间的摩擦。构件1、构件4和构件5分别为勾线臂、勾线座和勾线针，构件1和构件5通过构件4固定在一起构成一个运动构件。

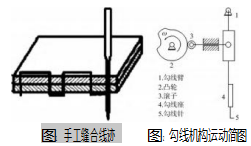
　　首先，利用SolidWorks创建凸轮的基本模型，即凸轮外圆和滚子；将其以大地坐标点为参考，使凸轮外圆零件坐标的原点（凸轮外圆中心）与大地坐标重合。如图3所示，设定凸轮的旋转方向及速度，保证在1min内旋转一整圈，即旋转速度为6(°)/s。

　　为了满足对滚子运动特性的需要，设定滚子的上下移动速度。如图4所示，对滚子进行线性马达驱动，其轨迹用线段控制，实际中从动件的运动规律如表1所示，将其角度和位置关系转换为时间和位置的关系，从而获得滚子的运动轨迹。

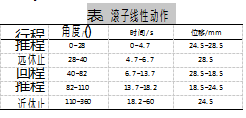
　　不同工作环境对凸轮廓线有不同的要求,珠边机勾线凸轮是在轻载高速的情况下工作，如表2所示，研究范围确定在正弦加速度和多项式。在运动规律的选择中为了避免冲击，针头推杆不宜采用加速度突变的运动规律。

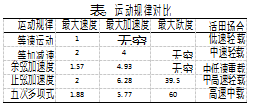
　　改变凸轮不同时段的线形，可以得到不同的运动学特性。在设计中只要保证加速度的连续就能保证凸轮不受到过大的冲击。经过分析，各个公式下的加速度曲线都是连续的，发现正弦曲线的窜动最小，由于高次的多项式廓线加工成本过高，低次的多项式廓线跃度较大。所以本次对凸轮的设计采用正弦函数的运动规律。

　　如图5所示，利用反转法设计出从动件滚子的运动轨迹，使凸轮反转最后得到滚子中心点的运动轨迹。将其曲线导入CAD中对其进行等距偏移，导入SolidWorks中进行切除就能得到凸轮的实际廓线。

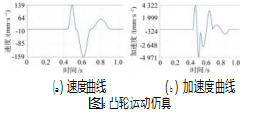
　　如图6所示，将装配后的组件进行仿真，转速为60 r/min,得到其速度和加速度曲线。

　　2 MATLAB运动学分析

　　正弦曲线的推程运动方程为：

　　s=h[(δ/δ0)-sin(2τδ/δ0)/2τ](1)

　　v=hω[1-cos(2τδ/δ0)]/δ0(2)

　　a=2τhω2 sin(2τδ/δ0)/δ(3)

　　j=4τ2 hω3 cos(2τωt/δ0)/δ(4)

　　回程方程为：

　　s=h[1-(δ/δ1)+sin(2τδ/δ1)/(2τ)](5)

　　v=hω[cos(2τδ/δ1)-1]/δ1(6)

　　a=-2τhω2 sin(2τδ/δ1)/δ(7)

　　j=-4τ2 hω3 cos(2τωt/δ1)/δ(8)

　　式中：s为从动件位移；h为行程高度；δ为此时的角位移；δ0为该行程的弧度；v为从动件速度；ω为凸轮的旋转速度；a为从动件加速度；j为从动件跃度；t为时间。

　　凸轮的曲线如图7所示。

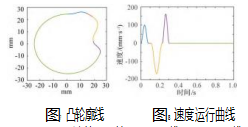
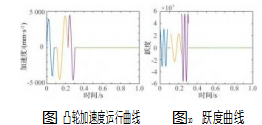
　　用MATLAB计算出凸轮的速度曲线和加速度曲线如图8~9所示。当转速达到1440 r/min可以看到速度、加速度曲线是连续的，说明凸轮运动平滑、冲击小。

　　用MATLAB计算凸轮廓线跃度的曲线，如图10所示，曲线窜动较小，说明凸轮有很好的运动特性，能满足高速轻载的冲击要求。

　　3疲劳分析

　　疲劳按种类分类可以分为高周疲劳和低周疲劳，其中高周疲劳是指应低于材料屈服点的应力，在循环次数大于105的循环中发生的破坏。低周疲劳则是在局部应力超过屈服点且循环次数在103以下发生破坏。因为循环应变在疲劳中起着主导的作用，所以，低周疲劳也被称作为塑性疲劳。由于凸轮工作环境为轻载高速的环境，以高周疲劳为主导，零件表面在接触应力循环作用下出现麻点、剥落或表层也随剥落，从而造成零件失效的疲劳。所以，对凸轮进行疲劳分析是很有必要的。

　　首先，单独将凸轮机构进行动力学分析，如图11所示，为了简化计算，且为了保证工件的安全等级，假设推杆F受力为1.5 N。

　　凸轮压力角如图12所示。通过达朗贝尔原理，建立动力学模型。

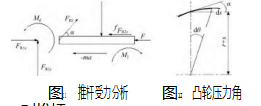
　　对推杆：

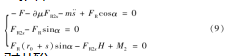
　　对凸轮：

　　经过简化分析和计算，建立边界条件，其中δ为表征摩擦方向的量，当从动件速度大于0,δ=1,当从动件速度小于0,δ=-1。

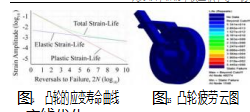
　　凸轮的网格划分如图13所示。凸轮工作环境所用电机型号为GMT5522,其额定功率为550 W,频率为50 Hz,额定转速为1440 r/min。经过传动后，到凸轮位置传动比为1/6。凸轮转速为240 r/min。材料为45钢，其属性如表3所示。材料的应变寿命曲线如图14所示。凸轮疲劳云图如图15所示。经过观察，凸轮最小寿命为2.855×1013。

　　4廓线优化

　　本文采用七次多项式系数为优化目标，通过优化凸轮廓线以达到优化模型受应力的情况，从而延长凸轮寿命。七次多项式凸轮运动参数公式如下所示。

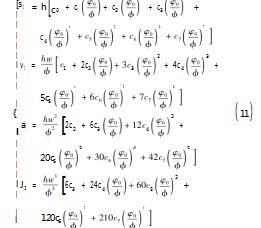
　　凸轮与滚子接触处受应力变化公式为：

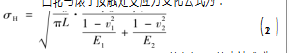
　　可见对应力最大影响的是F的大小，FR的表达式为：

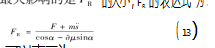
　　其中α可以表示为：

　　为此建立单目标规划模型，以加速度为优化目标，以七次多项式系数为优化对象，通过模拟退火算法，进行优化。

　　模拟退火算法具有一定局限性，其只能对有限的解经过公式变形后，得到新解。这里需要对其进行一定的调整，增加约束条件且需要求出一组新解产生的公式的最大值。

　　对于增加约束条件，取当φ0=φ,存在，S1=h。可推导出：

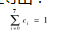
　　且φ0=1,S1=0可以推导出：c0=0。

　　为保证速度、加速度、跃度的连续性需要保证c0=c1=c2=c3=0。

　　因为曲线连续，采用逐个带入的方法，当做求解产生新解后廓线最大加速度的方法。

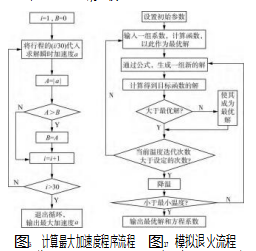
　　流程依次取坐标上30个点，求解比较，流程如图16所示。
       建立的数学模型为：

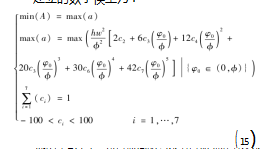
　　通过以上公式，可以把问题简化为以加速度为优化目标，建立单目标规划模型。其流程如图17所示。

　　因为只需要优化c4、c5、c6、c7生成新解的公式流程为：首先生成1行6列的0~1的随机数用以计算cnew4、

　　c new5、c new6;

　　a=randn(1,6)

　　根据新解的产生规则计算Zi:

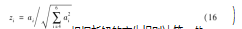
　　T为当前温度，根据新解的产生规则计算c的值。

　　c newi=c i+Zi×T

　　c new7=1-c new4-c new5-c new6

　　初始条件：模拟退火的初始条件为，初始温度为200,最大迭代次数为5000,每个温度下的迭代次数为300,温度衰减系数为0.95。

　　最终优化后的曲线迭代结果为：c 1=0,c2=0,c3=0,c4=6.212 7,c5=-7.053 1,c6=1.891 9,c7=-0.051 5。

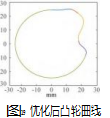
　　画出其运动学参数曲线如图18所示，廓线如图19所示。

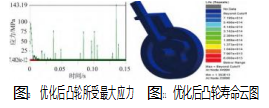
　　将模型代入Workbench平台进行动力学分析（图20~21),其等效应力变化相对以前较小，在Ncode模块中，得到仿真得到结果为4.14×10 14。最小寿命提升了14倍左右。

　　5结束语

　　本文以特种缝合设备珠边机的仿手工线迹缝合勾线机构工作过程为例，对高速轻载环境下的凸轮设计方法及疲劳分析进行了深入研究，取得了如下结果。

　　(1)在特种缝合装备珠边机勾线机构设计中，对不同凸轮廓线进行了对比论证，选取正弦凸轮进行了运动学、动力学和疲劳分析。因为高速轻载的工况，正弦廓线的凸轮疲劳耐久度不能达到要求，为此采用七次多项式优化后的廓线进行优化。

　　(2)通过分析七次多项式廓线的加速度和凸轮所受应力的关系，以凸轮最大加速度为优化目标，以凸轮七次系数为变量，通过对模拟退火算法的改进和应用，经过多次迭代，得到了最优解，以此为系数建立凸轮的七次多项式廓线。

　　(3)经过疲劳分析，验证了优化后的凸轮寿命相比未优化前提高到了14倍左右，并且采用优化后的七次凸轮廓线设计会得到更好的运动学性能。

   　参考文献：

　　[1]孙桓．机械原理[M].北京：高等教育出版社，2022.[2]洑良贵．机械设计[M].北京：高等教育出版社，2019.

　　[3]高玉刚，吴海艳，赵付斌．喷气织机打纬机构用共轭凸轮设计[J].纺织器材，2023,50(6):33-37.

　　[4]连聚键．盘形凸轮机构在自动化设备中的应用[J].内燃机与配件，2020(24):102-103.

　　[5]梅宝龙，袁汝旺．剑杆织机用凸轮机构设计[J].纺织器材，2021,48(4):1-4.

　　[6]邱海飞，李春风，陈铭，等．一种外置式高速织机共轭凸轮开口设计[J].机械设计，2022,39(11):1-6.

　　[7]刘健，安法金，侯玉秋，等．碳纤维仿手工线迹缝合机针力学性能分析及优化设计[J].毛纺科技，2023,51(8):89-95.

　　[8]朱育权，李大印，尚涵涵．直动从动件平面移动凸轮机构的动力学优化设计[J].西安工业大学学报，2019,39(5):527-533.

　　[9]金国光，陈家猛，魏展，等．从动件运动规律对凸轮机构接触碰撞运动特性影响研究[J].河南理工大学学报：自然科学版，2021,40(6):108-116.

　　[10]王仲勋，蒲洁涛，娄红杰，等．基于SolidWorks的凸轮机构设计及运动仿真[J].机械工程师，2021(10):117-118.

　　[11]池宁骏．计算机辅助产品设计SolidWorks教程[M].北京：化学工业出版社，2018.

　　[12]林巨广，程刚，刘凯，等．凸轮的新型精确设计及加工方法[J].机械工程师，2012(3):54-55.

　　[13]田绿竹，霍平．基于MATLAB的凸轮机构设计及仿真软件的开发[J].机电一体化，2009,15(4):95-96.

　　[14]ANINDYA G.Kinematic analysis of different shedding cams used in weaving looms[J].Iranian Endodontic Journal,2019,12(12):101-103.

　　[15]GIORDANA F,ROGNONI V,RUGGIERI G.On the influence of measurement errors in the kinematic analysis of cams[J].Mechanism&Machine Theory,1979,14(5):327-340.

　　[16]BURGOS A,MIRANDA E,VILAPRINYO E,et al.CAM models:lessons and implications for CAM evolution[J].Frontiers in Plant Science,2022(13):23-26.

　　[17]王浙标．手工线迹在服装设计中的应用研究[D].北京：北京服装学院，2019.

　　[18]YANG Y H,XIE R,WANG J Y,et al.Design of a novel coaxial cam-linkage indexing mechanism[J].Mechanism and Machine Theory,2022(169):77-81.

　　[19]TIBONI M,AMICI C,BUSSOLA R.Cam mechanisms reverse engineering based on evolutionary algorithms[J].Electronics,2021,10(24):83-88.

　　[20]韩玉林．基于U G的圆锥凸轮模型全参数化设计[J].机电工程技术，2019,48(3):28-29.