摘要：深埋煤层巷道围岩的塑性区形态及范围对煤矿生产安全具有重要意义。本文以山西某矿150505工作面顺槽为研究背景，通过理论分析的手段，研究了侧压系数和应力偏转角度对圆形巷道围岩塑性区形态的影响规律。研究结果表明：在非等压应力场下，巷道围岩会呈现圆形、椭圆形、蝶形三种形态，当巷道围岩形成蝶形塑性区时，围岩的塑性区较大；巷道围岩的塑性区偏转程度与围岩主应力偏转程度存在一一对应关系，塑性区的偏转角度与主应力偏转角度基本一致；当蝶形塑性区最大尺寸蝶叶旋转至巷道上方时，巷道容易产生冒顶，这也是巷道围岩产生非对称破坏的原因所在。目前的现有支护能力无法减小巷道围岩塑性区，但可以较好地控制顶板围岩形成冒顶。

　　关键词：蝶形破坏；塑性区；巷道支护；冒顶；大变形破坏

　　0引言

　　随着对能源需求的增加，浅埋煤层的资源逐渐减少。目前大部分矿区已经开始向深部发展。因此研究深部巷道围岩的稳定性问题具有重要意义。

　　针对巷道围岩的塑性区求解问题及巷道围岩的稳定性控制问题，众多学者展开了大量的研究。康红普[1]等总结了支护—改性—卸压“三位一体”复杂困难巷道围岩控制理念；介绍了我国冲击地压监测预警设备和平台与冲击地压防治技术体系、覆岩破坏理论与地表沉陷计算模型与方法及煤矿岩体采动响应理论与特殊开采技术体系。苏士龙[2]等通过UDEC软件对比了细观参数校核及无支护状态的宏观物理-数值模型,提出了“锚杆+锚索+喷射混凝土+工字钢”成套支护方法,为工程中的矩形巷道层状围岩稳定性控制提供参考。赵庆冲[3]等对巷道围岩稳定性进行分类，判别巷道支护设计方案的有效性，对煤矿的安全生产提供参考。蔡美峰[4]介绍了采矿工程中地应力荷载作用方式的特殊性与地应力控制采矿开挖过程和岩层稳定性的力学机理。认为开挖引起地应力形成“等效释放荷载”，从而带动周围岩体产生变形和应力集中。赵志强[5]等以弹塑性力学中孔洞围岩破坏的平面应变模型为基础研究圆形巷道围岩塑性区形态和扩展规律，得出了“蝶形塑性区”理论公式并提出了巷道围岩蝶形破坏理论，给出了巷道围岩三种基本破坏形态的数学界定标准和应力围岩判别准则及蝶形塑性区的基本特性。康红普[6]等针对煤矿千米深井、软岩、强采动的巷道围岩大变形难题，研究了高地应力与超长工作面强采动应力叠加作用下巷道围岩大变形机理。刘洪涛[7]等通过引入Lode角参数推导出考虑巷道轴向应力影响的圆巷围岩塑性区近似解，对蝶形破坏理论做了进一步完善。

　　本文基于蝶形破坏理论，以山西某矿深埋煤层为工程背景，通过理论分析回风巷围岩产生非对称变形破坏机理的原因，并对蝶形塑性区的支护思路进行探究，对非对称大变形巷道提供围岩稳定控制建议。

　　1工程背景及巷道围岩塑性区求解

　　1.1工程背景

　　某矿150505综采工作面，位于0205采区东翼，以东为构造发育区域；以西为0205采区巷道；以南为尚未开掘的150507工作面；以北15 m为150503采空区，水平位置为+858 m，煤层名称为15#，上部为8+9#煤层090505采空区，层间距67～72 m。地面标高为1 141～1 215 m，工作面标高905～932 m。工作面走向长288 m，倾向长159 m，可采区平面积49 109.9 m2。

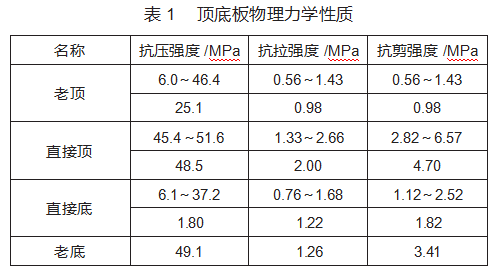
　　150505工作面老顶岩层为砂质岩石，厚度为11.47 m，灰黑色砂质泥岩，在234.60 m有错动，含黄铁矿，云母；直接顶岩层为石灰岩，厚度为1.31 m，深灰色石灰岩，含方解石脉，黄铁矿，动物化石；直接底岩层为砂质岩石，厚度为4.84 m，黑色砂泥岩，顶0.40 m为泥岩，含黄铁矿及钙质；老底岩层为细粒砂岩，厚度为3.88 m，深灰色细砂岩，石英、云母为主，含炭质层面，少许黄铁矿。其主要力学性质如表1所示：

　　根据工作面掘进情况现场调研可知，该工作面附近断层及陷落柱较发育，且由于埋深较大，巷道在采动应力及构造应力的叠加影响下，巷道破坏呈现非对称大变形破坏，局部出现严重冒落。

　　1.2巷道围岩塑性区边界方程

　　回采巷道的塑性破坏问题一般简化为平面应变问题，极坐标下巷道任意一点的主应力计算如公式（1）所示：

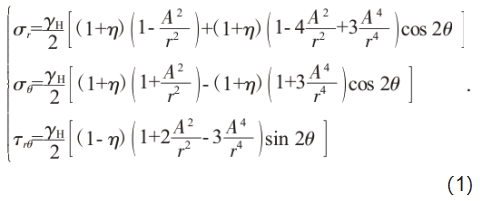
　　式中：σθ为任一点的环向应力，MPa；σr为任一点的径向应力，MPa；τrθ为任一点的剪应力，MPa；γH为巷道竖向载荷，MPa；η为侧压系数；A为圆形巷道半径，m；r、θ为任一点的极坐标。

　　巷道围岩任意一点的破坏与否取决于强度准则，目前使用较为广泛的是摩尔库伦强度准则，摩尔库伦强度准则表达式如式（2）所示：

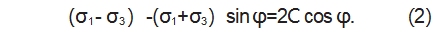
　　基于上述公式即可求得巷道围岩任意一点的塑性区边界八次隐性方程如式（3）所示：

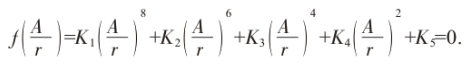
　　式中：A为圆形巷道半径；r为对应θ角度处的塑性区深度；

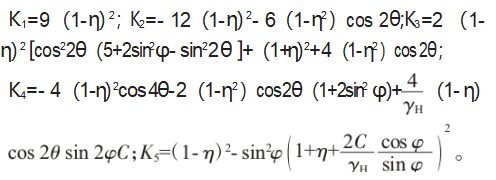
　　研究工作面平均埋深918.5 m，根据矿压即可计算求垂直应力为22.96 MPa。在工作面开采过程中，原岩应力平衡被打破，采空区四周形成支承压力带，应力增高系数可达3倍以上。因此，研究合理应力范围内的塑性区形态及尺寸演化特征具有重要意义。

　　采用控制变量法，固定垂直应力SZZ=22.96 MPa，取侧压系数为1.0~2.8，将数据带入塑性区边界方程即可求得塑性区形态及尺寸演化规律如图1所示。

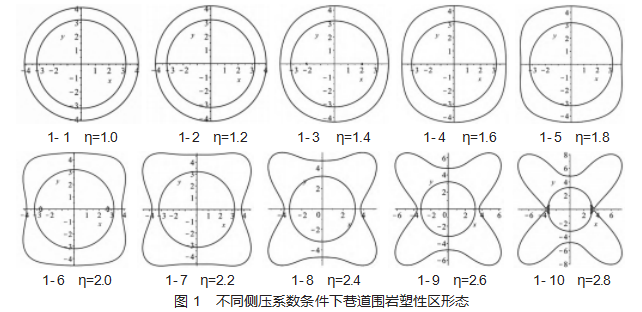
　　由图1形态图可以看出，当围压比值为1.0时，巷道围岩塑性区为标准的圆形形态，当围压比值为1.2、1.4时，塑性区形态为类椭圆形态，当侧压系数为1.6时，围岩塑性区形态开始出现“蝶形”轮廓，四个象限的角平分线附近开始产生小量扩展，随着围压比值的继续增加，巷道蝶形形态逐渐明显。

　　对不同侧压系数条件下的围岩塑性区尺寸进行分析来看，侧压系数为1.0时，围岩各处的塑性区尺寸完全相同，随着侧压系数的增加，围岩坐标纵轴（顶底板）方向的塑性区尺寸不断扩展，横轴（两帮）方向的塑性区尺寸不断减小。随着侧压系数的增加，巷道四个象限角平分线附近的塑性区尺寸开始扩展，扩展速度由缓到急，到侧压系数较大时开始形成恶性扩展。

　　综上分析可以看出，当巷道围岩形态为圆形或者椭圆形时，围岩塑性区尺寸相对较小，处于普通锚杆可控的支护范围内；当巷道围岩为蝶形形态时，塑性区尺寸相对较大，巷道围岩的破坏范围超出正常支护体的支护范围。因此要重视巷道形成蝶形塑性区，防止形成大范围破坏。

　　此外，工作面推进过程中，顶板垮落会导致应力偏转，因此研究主应力偏转条件下的巷道围岩塑性区具有重要意义。通过数学软件得不同偏转角下的巷道围岩塑性区如红色曲线如图2所示。

　　图2中黑色曲线为应力偏转角为0。时的塑性区，红色曲线产生不同应力偏转角的塑性区形态。从图2可以看出，蝶形塑性区蝶叶会随着主应力偏转而偏转，应力偏转角与塑性区偏转角存在一一对应关系。当主应力偏转角转过转过某个角度时，塑性区也基本转过同样的角度。

　　由上述分析也可以看出，当应力偏转角度为0O时，蝶叶最大塑性区尺寸位于巷道45O附近，当巷道主应力产生偏转时，蝶叶开始产生旋转，此时巷道开始产生非对称破坏，这就是深埋巷道产生非对称大变形破坏的原因。

　　2蝶形塑性区支护机理探究

　　在经典的矿压理论中，目前有一些较为经典的理论，如悬吊理论、组合梁理论、组合拱理论、最大水平应力理论、围岩强度强化理论、巷道围岩蝶形破坏理论。这些理论对巷道围岩的稳定控制具有重要意义。

　　文献[8]通过岩土工程软件FLAC3D对巷道围岩稳定性进行分析，通过改变锚杆索支护密度来研究巷道塑性区的变化，由图3可以看出，巷道围岩塑性区并不会随着锚杆索密度的增加而呈现明显的变化趋势。

　　由此可以看出，在目前的支护水平下，普通支护体的支护能力还无法与采动应力等应力的量级相匹配，锚杆索的支护作用主要是将上部较为软弱的岩层悬吊在上部稳定岩层之上，增强软弱岩层的稳定性，防止产生大面积冒顶。

　　3结论

　　1）在非等压应力场下，巷道围岩会呈现圆形、椭圆形、蝶形三种形态，当巷道围岩形成蝶形塑性区时，围岩的塑性区尺寸一般都比较大。

　　2）巷道围岩的塑性区偏转程度与围岩主应力偏转程度存在一一对应关系，塑性区的偏转角度与主应力偏转角度基本一致。当蝶形塑性区最大尺寸蝶叶旋转至巷道上方时，巷道容易产生冒顶。

　　3）目前的现有支护能力无法减小巷道围岩塑性区，但可以较好地控制顶板围岩形成冒顶。

　　参考文献

　　[1]康红普，徐刚，王彪谋，等.我国煤炭开采与岩层控制技术发展40 a及展望[J].采矿与岩层控制工程学报，2019，1（1）：7-39.

　　[2]苏士龙，杜跃，朱俊福，等.基于离散元方法的深部巷道层状围岩稳定特性研究[J].采矿与岩层控制工程学报，2020，2（1）：56-66.

　　[3]赵庆冲，付宝杰.受动压影响巷道围岩松动圈测试及支护技术研究[J].采矿与岩层控制工程学报，2020，2（2）：49-56.

　　[4]蔡美峰.深部开采围岩稳定性与岩层控制关键理论和技术[J].采矿与岩层控制工程学报，2020，2（3）：5-13.

　　[5]赵志强，马念杰，刘洪涛，等.巷道蝶形破坏理论及其应用前景[J].中国矿业大学学报，2018，47（5）：969-978.

　　[6]康红普，姜鹏飞，黄炳香，等.煤矿千米深井巷道围岩支护-改性-卸压协同控制技术[J].煤炭学报，2020，45（3）：845-864.

　　[7]刘洪涛，韩子俊，郭晓菲，等.考虑轴向应力影响的圆巷围岩塑性区近似解[J].煤炭科学技术，2023，51（10）：12-23.

　　[8]李臣，霍天宏，吴峥，等.动压巷道顶板非均匀剧烈变形机理及其稳定性控制[J].中南大学学报（自然科学版），2020，51（5）：1317-1327.