摘要：为了研究丝杠转速、轴向载荷、螺旋升角和滚珠直径对摩擦力矩的影响规律，在综合考虑滚珠载荷分布、实际工况中接触角变化、法向力差异、润滑油黏性阻力、滚珠惯性力和惯性力矩等因素上，建立了一种计算滚珠丝杠副摩擦力矩的方法。结果表明：当丝杠转速或轴向载荷增大时，摩擦力矩越来越大；增大的轴向载荷或者减小的丝杠转速导致摩擦因数越来越小；随着螺旋升角变大时，摩擦因数和摩擦力矩均逐渐减小，且随着螺旋升角的增大，两者的变化率逐渐减小；滚珠直径的变大致使摩擦力矩变大。分析结果可为滚珠丝杠副的设计提供参考，有助于进一步提高滚珠丝杠副的传动性能。

　　关键词：滚珠丝杠副；摩擦力矩；接触角；螺旋升角；载荷分布

　　0引言

　　滚珠丝杠副被广泛应用于数控机床、精密仪器、航空飞机等机械行业中[1-3]，近些年高精度、高效率、高速化的发展趋势对滚珠丝杠副的性能提出了更高的要求，摩擦力矩为衡量滚珠丝杠副传动性能的指标之一，由其产生的能量损耗会造成传动效率下降，丝杠会因温度升高而发生热变形[4]，从而影响其寿命和定位精度。所以，对滚珠丝杠副摩擦力矩的研究在机械领域内具有重大意义。

　　在滚珠丝杠副摩擦力矩研究方面，Wei等[5]分析了变接触角工况下的滚珠丝杠副运动特性和弹性变形，其后面的摩擦因数、摩擦力的计算方法是由4个关联坐标的建立及其转换关系得出。Olaru等[6]在分析丝杠转速和轴向载荷对总摩擦力矩的影响时采用了数值计算方法，结果显示载荷和丝杠转速变大时，摩擦力矩也随之变大，但两者对摩擦力矩作用效果的主次关系并没有提出。Zhang等[7]通过分析滚珠与滚道接触点的误差对接触力的影响，进一步研究了精密滚珠丝杠副摩擦力矩的稳定性，认为摩擦力矩的均值受到加工误差的影响，摩擦力矩的波动可通过合理的润滑来减小。陈勇将等[8]基于滚珠丝杠副的摩擦机理，针对不同转速下摩擦力矩的变化规律，通过力与力矩平衡进行了分析解答，结果表明润滑介质的性能参数是主要影响因素。孙铁伟[9]基于等温弹流润滑理论建立了滚珠丝杠副弹流润滑接触模型，研究表明丝杠转速越高，润滑状态越好，那么在生产过程中可以通过调整丝杠转速使其处于弹流润滑状态来降低损耗。

　　上述研究均假设滚珠所受载荷相同，而实际中各个滚珠的受载存在一定的分布规律。滚珠承受载荷大小不同，导致滚珠与螺旋滚道的接触角、接触变形以及滚珠与螺旋滚道产生的摩擦力矩均会存在差异，故在假设滚珠载荷均布的情况下分析摩擦力矩会偏离实际情况。因此，在分析摩擦力矩之前，有必要先对载荷分布进行研究。靳谦忠等[10]研究的滚珠丝杠副的载荷分布规律是在半螺距内滚珠受载均匀的假设下完成的。Mei等[11]对滚珠丝杠副载荷分布的影响是受加工误差的作用进行了研究。

　　本文首先基于Hertz接触理论，求得滚珠丝杠副中滚珠的载荷分布。然后，综合考虑实际工况中接触角的变化、法向力的差异、润滑油的黏性阻力、滚珠惯性力和惯性力矩等因素，建立滚珠丝杠副力与力矩平衡关系式，提出了一种考虑滚珠载荷分布的摩擦力矩计算方法。在此基础上，对比了考虑滚珠载荷分布和假设滚珠载荷均布的条件下，丝杠转速和轴向载荷对摩擦力矩的影响。最后，基于本文方法研究了滚珠丝杆副摩擦因数和摩擦力矩受轴向载荷、丝杠转速和螺旋升角的影响规律，分析了滚珠直径对摩擦力矩的影响规律。

　　1滚珠载荷分布计算方法

　　1.1 Hertz接触变形

　　在滚珠载荷分布计算中，做如下假设[10]：（1）假定接触角不变，变形导致的接触角变化不予计算；（2）认定滚珠与螺母接触的法向载荷和滚珠与丝杠接触的法向载荷都一样。

　　根据Hertz理论可知，螺母与滚珠、滚珠与丝杠间接触面的接触变形δ可表示[12]为：

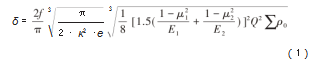
　　式中：Q为在接触面上作用的法向力；0为接触体的主曲率；E1、E2分别为相接触两物体的弹性模量；μ1、μ2分别为两接触体泊松比。

　　式中：ρ11和ρ12分别为在滚珠与螺母或丝杠滚道接触点处滚珠的第一和第二主曲率；ρj21和ρj22分别为在滚珠与螺母或丝杠滚道接触点处螺母或丝杠滚道的第一和第二主曲率。

　　滚珠与丝杠滚道的接触点用s表示，滚珠与螺母滚道的接触点用n表示。

　　式中：d为滚珠直径；d0为滚珠丝杠副的公称直径；α为滚珠与螺母或丝杠滚道的接触角；λ为丝杠的螺旋升角。

　　式中：δsi为滚珠与丝杠接触侧的第i个接触变形；δni为滚珠与螺母接触侧的第i个接触变形；Cs为丝杠的接触刚度；Cn为螺母的接触刚度；Qi为滚珠与滚道接触处第i个法向载荷。

　　1.2滚珠丝杠副轴向弹性变形

　　将滚珠丝杠副的丝杠和螺母都当作圆柱处理，丝杠和螺母的轴向变形分别为：

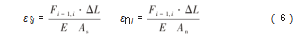
　　式中：εsi为丝杠段在第i-1个滚珠和第i个滚珠之间的轴向变形；εni为在第i-1个滚珠和第i个滚珠之螺母段的轴向变形；E为在丝杠和螺母材料中的弹性模量；As为在接触处丝杠的横截面积；An为在接触初螺母的横截面积；ΔL为在相邻两个滚珠之间的轴向距离；Fi-1，i为在第i-1个滚珠和第i个滚珠之间丝杠段所承受的轴向载荷表示。

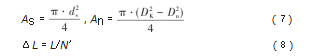
　　式中：ds为丝杠的有效直径；Dk为螺母外径；Dn为螺母有效直径；L为丝杠导程；N'为单个导程内的滚珠数。

　　将丝杠滚道沿轴向展开，可得丝杠沿轴向受力关系如图1所示。

　　其中，Fa为轴向工作载荷，Fi为第i个滚珠与丝杠滚道之间的轴向作用力。

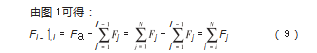
　　式中：N为滚珠丝杠副的滚珠个数。

　　滚珠与丝杠或螺母滚道之间的轴向力和法向力关系为[14]：

　　式中：α为滚珠和螺母或丝杠滚接触角道；λ为丝杠的螺旋升角。

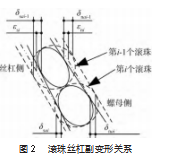
　　1.3滚珠载荷分布

　　如果将丝杠和螺母的变形等效为滚珠的变形，则滚珠丝杠副在第i-1个滚珠和第i个滚珠之间的变形关系如图2所示。图中变形前后的滚珠、丝杠滚道和螺母滚道的相对几何位置关系分别用虚线和实现表示，Hertz接触变形的轴向分量在第i-1个和第i个滚珠与螺母或丝杠滚道中分别用δjai-1和δjai表示（滚珠与丝杠的接触面用s表示，滚珠与螺母的接触面用n表示）。因此，可得变形协调关系式为：

　　式中：Qi为在第i个滚珠与滚道接触处的法向载荷；As为在接触处的丝杠横截面积；An为在接触处的螺母横截面积；ΔL为相邻2个滚珠之间的轴向距离；E为丝杠和螺母材料的弹性模量；Cs为丝杠接触刚度；Cn为螺母接触刚度；N为滚珠丝杠副中的滚珠个数；Fa为滚珠丝杠副轴向工作载荷。

　　2摩擦力矩计算方法

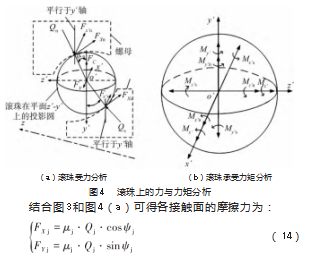
　　2.1滚珠丝杠副坐标系建立

　　建立滚珠丝杠副坐标系如图3所示[5][15]。图中，滚珠中心与建立的x'-y'-z'局部坐标系的坐标原点重合，切线方向在滚珠运动轨迹表示为x'轴，丝杠表面的垂直方向且指向内侧表示为y'轴，x'y'平面垂直于z'轴。接触坐标系Xj-Yj-Zj用来描述摩擦力的方向，丝杠和螺母的接触椭圆中心表示为坐标原点，滚珠在在z'-y'平面的节圆的切线方向表示为Xj轴，x'轴平行于Yj轴，接触平面的法线方向在接触点处表示为Zj轴，且背离或指向滚珠中心。αj和ψj分别为对应侧滚珠与接触面的接触角和滑动角。

       2.2摩擦力矩求解

　　在得到每个滚珠承受的轴向力后，求出对应滚珠在工作过程中承受的摩擦力矩，然后对各个滚珠的摩擦力矩进行矢量合成，即为滚珠丝杠副的摩擦力矩。

　　对滚珠丝杠副进行受力分析，如图4所示[16]。图4（a）中，Qs为丝杠侧滚珠所受法向力，Qn为螺母侧滚珠所受法向力，FXs、Fx's、FXn和Fx'n分别为对应坐标方向上丝杠和螺母作用在滚珠上的摩擦力，Fc为离心力，FV为润滑油的黏性阻力。图4（b）中，Mx'、My'和Mz'分别为对应坐标方向上的惯性力矩，Mx'j、My'j和Mz'j分别为对应坐标方向上的摩擦力矩。

　　式中：rb为滚珠半径；aj为滚珠与螺母或丝杠滚道的接触角；下标j为s或n，s表示滚珠与丝杠的接触面，n表示滚珠与螺母的接触面。

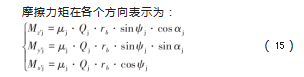
　　此外，通过滚珠丝杠副受力平衡关系可以迭代解出滚珠与接触面的滑动角Ψj、滚珠与滚道接触点的法向力Qj以及加载后滚珠与螺旋滚道之间的接触角αj，具体求解方法可分别参见文献[5]和[16]。

　　2.3黏性阻力和惯性力矩求解

　　由图4（b）可得滚珠在x'方向上的受力平衡关系式和力矩平衡关系式为：

　　式中：ε为有效流体密度在润滑油中；CV为在润滑油中阻力系数；ωm为在滚珠中的公转角速度；g为重力加速度。

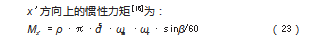
　　式中：ρ为滚珠密度；ωr为滚珠自转角速度。

　　联立式（19）~（23）可分别求得滚珠与丝杠和螺母间的摩擦因数μs、μn。分别求出滑动角Ψj、接触角αj和摩擦因数μj后，代入式（15）~（16）可求得单个滚珠在各个方向上的摩擦力矩。本文计算的滚珠丝杠副结构参数如表1所示。

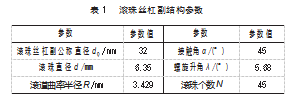
　　分别应用本文所建模型和文献[5]中假设载荷均布的摩擦力模型求解滚珠丝杠副在不同轴向载荷和丝杠转速下的摩擦力矩，如图5（a）所示。为了使得轴向载荷对摩擦力矩的影响更加显著，对摩擦力矩使用5 000 r/min转速下轴向载荷，得出影响曲线如图5（b）所示。由图5可知，2种方法计算的结果变化趋势一致，但考虑滚珠载荷分布时的摩擦力矩大于假设滚珠载荷均布情况下的摩擦力矩，同时，越来越高的丝杠转速或越来越大的轴向载荷，会导致2种模型下摩擦力矩的差值也逐渐变大。可见，弹性变形造成的载荷分布对滚珠丝杠副摩擦力矩的影响是本文方法所能表现出来的结果。从图5还可以看出，轴向载荷越大，影响摩擦力矩的丝杠转速也随之变大。因此，应该多方面考虑丝杠转速和轴向载荷的影响来分析摩擦力矩。

　　3摩擦力矩影响因素

　　3.1载荷分布中轴向载荷的影响

　　对应不同的轴向载荷，滚珠的载荷分布如图6所示。由图可知，滚珠丝杠副轴向载荷在各个滚珠上的分布呈现不均匀性，并且载荷分布不随着轴向载荷的增大而增大，呈现不均匀分布。所以，对滚珠丝杠副摩擦力矩进行分析时，滚珠载荷分布的影响有必要考虑进去。

　　3.2运行工况对接触角的影响

　　初始接触角在滚珠与滚道中为45°,且在轴向载荷和丝杠转速都对应不同时，滚珠与滚道接触点平均接触角αs和αn在具有载荷分布情况下得出的规律变化如图7所示，其中接触角在滚珠与丝杠滚道中是αs，接触角在滚珠与螺母滚道中是αn。由图可知，保证一定的轴向载荷，丝杠转速变大后接触角αs也变大，但丝杠转速变大后接触角αn却变小。此外，轴向载荷在变大时，接触角αs和αn的变化幅度变小；丝杠转速变大时，接触角接触角αs和αn之间的差值也随之变大，因此两侧接触角不能在丝杠转速较大时视为一样。接触角在丝杠转速大且轴向载荷小时会引起较大的变化，从而对其动态性产生较大的影响，相反，接触角在轴向载荷大且丝杠转速小时的变化较小，αs和αn趋于相等。

　　3.3运行工况对摩擦力矩的影响

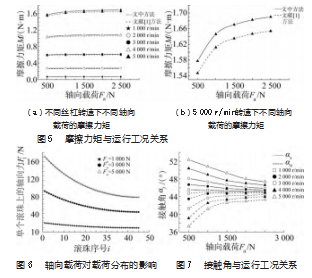
　　对应不同轴向载荷和丝杠转速求解摩擦因数，求得考虑载荷分布情况下不同运行工况对平均摩擦系数的影响规律，如图8所示。其中，μs为滚珠与丝杠滚道的摩擦因数；μn为滚珠与螺母滚道的摩擦因数。由图可知，μs大于μn；在相同丝杠转速下，摩擦因数随轴向载荷减小而变大，且轴向载荷越小两侧摩擦因数的差值越大。当轴向载荷相同时，丝杠转速变大使得摩擦因数μs和μn变大，其差值也随着丝杠转速的增大而增大。这是因为转速升高或轴向载荷减小增加了滚珠与滚道接触面间的滑动效应，同时，转速升高也会增大润滑油的黏性阻力。

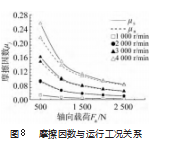
　　同时，图8间接验证了图5所得结论：轴向载荷变大或者丝杠转速上升使得摩擦力矩变大，并且摩擦力矩受轴向载荷的影响比较小。滚珠与丝杠或螺母滚道接触面的接触力尽管随轴向载荷的增大而变大，但同时减小了丝杠侧和螺母侧的摩擦因数。

　　3.4螺旋升角和滚珠直径对摩擦力矩的影响

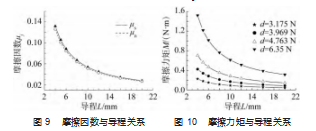
　　在滚动螺旋传动机构中，在滚珠螺旋传动机构中，由导程求得螺旋升角，且在其他结构参数保持不变的情况下，只有导程影响螺旋升角。取轴向载荷Fa=1 500 N，丝杠转速n=3 000 r/min，计算在不同导程（螺旋升角）下的摩擦因数，可以得到在考虑载荷分布情况下平均摩擦因数μs和μn随导程变化的曲线如图9所示，其中μs为滚珠与丝杠滚道的摩擦因数，μn为滚珠与螺母滚道的摩擦因数。由图可知，摩擦因数μs和μn都随导程（螺旋升角）的增大而减小。在导程为4~12 mm，即螺旋升角为2.28°~6.81°,μs和μn下降速度很快；在导程为12~20 mm时，即螺旋升角为6.81°~11.25°,μs和μn下降速度变缓。

　　保持轴向载荷和丝杠转速不变，对应不同滚珠直径和导程（螺旋升角）求解滚珠丝杠副的摩擦力矩，求得考虑载荷分布情况下滚珠直径和导程（螺旋升角）对摩擦力矩的影响规律，如图10所示。从图可知，摩擦力矩随导程（螺旋升角）的增大而减小，且随着导程（螺旋升角）的增大，摩擦力矩的变化率逐渐减小。这是因为导程（螺旋升角）增大，降低了滚珠的滑动效应，减小了摩擦因数，从而使总摩擦力矩下降。当滚珠直径增大时，力臂增大，摩擦力矩也随着增大。所以，在设计滚珠丝杠副时选择合适的导程（螺旋升角）和滚珠直径，可以作为重要途径来降低摩擦力矩。

　　4结束语

　　本文在分析滚珠丝杠副载荷分布规律的基础上，提出了一种摩擦力矩计算方法，进而研究了丝杠转速、轴向载荷、螺旋升角以及滚珠直径对滚珠丝杠副摩擦力矩的影响规律。研究得到的主要结论如下：考虑滚珠载荷分布时的摩擦力矩大于假设滚珠载荷均布情况下的摩擦力矩，2种情况下的摩擦力矩随着丝杠转速的变大逐渐增大。丝杠侧摩擦因数大于螺母侧，且轴向载荷的变大使得两侧摩擦因数变小，丝杠转速的变大使得两侧摩擦因数变大，螺旋升角的增大使得摩擦因数随之变小。保持一定的转速，轴向载荷的变大使得摩擦力矩增大，但变化较小。保持一定的载荷，丝杠转速的变大使得摩擦力矩增大。轴向载荷越大，摩擦力矩受到丝杠转速的影响也就越大，由此看来丝杠转速也是影响摩擦力矩的重要因素。螺旋升角的增大使得摩擦力矩变小，且变化率逐渐减小，随着滚珠直径的增大而增大。因此，可以通过合理设计滚珠直径和螺旋升角来减小摩擦力矩。

　　参考文献：

　　[1]徐淑俭.滚珠丝杠副精度保持性试验台研究及测试系统开发[D].济南:山东建筑大学,2017.

　　[2]王志民,张西忠,厉勇.滚珠丝杠传动使用与发展[J].机电工程技术,2004,33(9):88-90.

　　[3]肖正义.滚珠丝杠副在航天航空领域的应用[J].制造技术与机床,2009(4):39-41.

　　[4]张国.滚珠丝杠副热变形问题研究与对策[J].现代制造技术与装备,2019(11):41-43.

　　[5]WEI C C,LIN J F.Kinematic analysis of the ball screw mecha-nism considering variable contact angles and elastic deformations[J].Journal of Mechanical Design,2003,125(4):717-733.

　　[6]Olaru D,Puiu G C,Balan L C,et al.A new model to estimate fric-tion torque in a ballscrew system[C]//Advanced Summer Institute on Product Engineering-Eco-Design Technologies and Green Energy Conference.Brasov Romania:Product Engineering-Eco-Design,Technologies and Green Energy,2004,231-240.

　　[7]ZHANG Z Y,ZHANG W L,SONG X C.Research on the stabili-zation of friction torque of precision ball screw[C]//2009 Interna-tional Conference on Mechatronics and Automation.Changchun.IEEE,2009:3716-3720.

　　[8]陈勇将,汤文成.微型滚珠丝杠副摩擦力矩模型的建立与实验验证[J].东南大学学报(自然科学版),2011,41(5):982-986.

　　[9]孙铁伟,王民,高相胜,等.基于等温弹流润滑理论的滚珠丝杠副摩擦机理研究[J].北京工业大学学报,2023,49(1):1-10.

　　[10]靳谦忠,杨家军,孙健利.滚珠丝杠副和行星式滚柱丝杠副静刚度的比较研究[J].机械科学与技术,1999,18(2):230-232.

　　[11]MEI X S,TSUTSUMI M,TAO T,et al.Study on the load distri-bution of ball screws with errors[J].Mechanism and Machine Theory,2003,38(11):1257-1269.

　　[12]Harris T A,Kotzalas M N.Rolling bearing analysis[M].Fifth Edition.Beijing:China Machine Press,2006:117-118.

　　[13]BREWE D E,HAMROCK B J.Simplified solution for ellipti-cal-contact deformation between two elastic solids[J].Journal of Lubrication Technology,1977,99(4):485-487.

　　[14]李凌丰,刘彩芬.滚珠丝杠副轴向变形分析[J].中国机械工程,2011,22(7):762-766.

　　[15]WEI C C,LIOU W L,LAI R S.Wear analysis of the offset type preloaded ball–screw operating at high speed[J].Wear,2012,292/293:111-123.

　　[16]WEI C C,LIN J F,HORNG J H.Analysis of a ball screw with a preload and lubrication[J].Tribology International,2009,42(11/12):1816-1831.