摘要：在数字助听器应用中，回声消除能力是检验助听器效果的标准之一。针对回声消除算法中自适应滤波器权重设置主观性较强以及实际语音信号波动性较大导致数字助听器回声消除精度不高的问题，提出了一种结合集合经验模态分解（EEMD）方法及鲸鱼算法（WOA）的最小均方误差算法（LMS）。该新方法在鲸鱼算法的基础上引入集合经验模态分解方法，采用集合经验模态分解方法将采集到的语音信号分解为若干个平稳的子序列，运用鲸鱼算法收敛速度较快的特点帮助自适应滤波器更快找到更适宜的权重，对自适应滤波器进行权重向量的优化，从而建立EEMD-WOA-LMS模型，通过回声消除效果的常用性能指标对所提方法进行验证。仿真实验表明，将改进方法与WOA-LMS算法相比，能获得较快的收敛速度和较低的失调量，并且均方误差有所降低，失调量降低了0.73 dB，回声损失值提升了2.87 dB，验证了EEMD-WOA-LMS算法的回声消除能力更优。

　　关键词：集合经验模态分解；自适应滤波器；鲸鱼算法；数字助听器；回声消除

　　0引言

　　传统的模拟助听器中，信号线性放大，易加大噪声污染[1]。随着现代技术的发展，模拟助听器逐渐被数字助听器取代，在数字助听器中，语音信号通过数字信号处理器（DSP）[2-3]相应的算法处理，可智能化选择需要的信号。但是由于助听器的传声器与受话器之间的距离较小，导致助听器使用过程中易产生回声现象从而影响患者佩戴体验[4]，因此以最小均方算法[5-7]为基础的自适应滤波算法成为助听器回声消除领域的研究重点[7]。

　　国内外学者针对数字助听器回声消除方面开展了诸多研究，孙祥娥等[9]通过引入误差信号控制步长因子，提出了一种改进的归一化最小均方算法，以加快滤波器收敛和降低稳态误差，但收敛速度仍旧不快。高纯等[10]针对数字助听器中回声消除算法复杂度高的问题，引入集员滤波理论以降低数字助听器的功耗，但功耗降低的同时使得回声消除能力不够。李双等[11]提出一种遗传算法优化BP神经网络的自适应回声消除算法，但遗传算法的若干参数的选择必须依靠经验且具有依赖性。Xu S等[12]针对大量回声的存在从而严重影响语音质量的问题，提出一种利用自适应滤波器和深度神经网络的多级声学回声消除模型，该模型虽然能够减弱回声问题，但大大加强了计算复杂度，无法适用于数字助听器类的小功率器件。赵轶骁等[12]使用粒子群算法对LMS算法的滤波参数进行优化，但粒子群算法可能导致参数在局部最优解附近陷入循环。

　　因此，本文针对数字助听器回声消除算法中自适应滤波器存在权重向量设置的主观性较强的问题，采用鲸鱼算法（WOA）对自适应滤波器的权值系数进行优化，基于适应度曲线自行设定最优权值，构建WOA-LMS模型。结合实际数字助听器实际收集来的音频进行分析，可以发现实际音频波动性较强，虽然较强的波动性可以较为容易被捕捉，但是较大的波动性在实际滤波中会产生较大的频谱影响，导致WOA-LMS算法不精，将集合经验模态分解方法引入该WOA-LMS模型，从而构建EEMD-WOA-LMS模型。最后，将该算法与其他优化算法进行比较，验证所提算法的有效性。实验证明，相比于原WOA-LMS算法，本文所提算法的收敛速度提高，均方误差降低，失调量下降0.73 dB，回声损失增益（Echo Return Loss Enhancement，ERLE）提高2.87 dB，性能取得了明显改善。

　　1助听器回声消除模型与LMS、WOA算法

　　1.1助听器回声消除系统模型

　　输出信号x(n)由原始信号s(n)经过放大增益通道后产生。x(n)经过真实反馈信道后产生回声信号y*(n)，y*(n)与噪声信号v(n)共同组成了麦克风的输入信号，即期望信号d(n)。x(n)经过估计回声路径后得到回声估计信号y(n)，误差向量由d(n)与y(n)做差得到。助听器回声消除模型如图1所示。

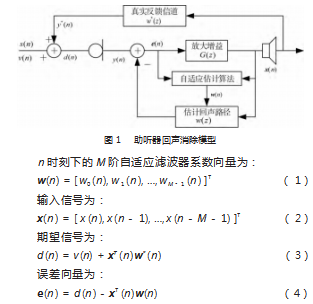
　　式中：T为转置运算；w*(n)为w(n)的复共轭，滤波器抽头权值向量w(n)由自适应算法确定，w(n)会根据误差信号e(n)自动调整。

　　1.2 LMS算法

　　LMS算法是自适应滤波中最为经典的一个算法，其迭代更新公式为：

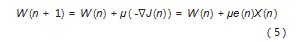
　　式中：μ为步长因子。

　　LMS算法采用单一步长μ,收敛速度较慢，导致助听器无法实时监听与处理语音信号，难以保持算法的稳定性[14]，因此提高自适应滤波器回声消除算法的可行性和可靠性是本论文研究的主要问题。自适应回声消除技术的核心思想就是原始信号经过麦克风采集，送入自适应滤波器，然后经过一系列的反馈函数来动态调节滤波器的系数，得到均方误差最小的输出信号[15]。

　　1.3 WOA算法

　　鲸鱼算法（WOA）[16]是2016年被提出的一种寻优算法，参考座头鲸捕猎的行为，通过在捕猎的过程中更新鲸鱼位置来寻找最优解，寻优过程的3个步骤分别为包围猎物、攻击猎物、搜索猎物[17]。

　　（1）包围猎物

　　式中：t为位置迭代的次数；X*(t)为最佳位置；X(t)为当前位置；A和C均为控制系数向量；D为座头鲸与猎物之间的距离。

　　式中：a为从2到0逐渐递减的值；r为0~1间的随机值。

　　（2）攻击猎物

　　鲸鱼捕食猎物的行为有螺旋向上的方式，数学模型表示为：

　　X(t+1)=X*(t)+Dpebl cos(2πl)        （10）
式中：Dp为最佳距离；b为螺旋状常数；l为(-1,1)中的任意数。

　　通过设置阈值Pi来决定鲸鱼以螺旋向上还是收缩环绕的方式更新位置，数学模型如下：

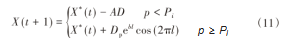
　　（3）搜索猎物

　　座头鲸在搜索猎物时，通过局部最优位置的不断更新，达到全局最优的目的，数学模型表示为[18]：

　　算法的位置更新方式由控制系数A来设定，当A≥1时，位置更新方式为式（13）；当A<1时，位置更新方式采用式（11）。

　　1.4 WOA-LMS模型构建

　　根据式（5），对于每一次迭代，步长μ和误差e都在变化，利用LMS更新公式更新滤波器系数w，利用WOA算法寻优自适应滤波器中每一个滤波器的权重，在范围内找到适应度函数的最优曲线，当均方误差最小时，μ最优，从而帮助自适应滤波器更快找到最优的权重，具体流程步骤如图2所示。当迭代次数达到最大值时迭代停止，输出当前位置即为最优解；若未达到，则继续寻优鲸鱼位置。WOA优化算法操作简单，通过对控制系数A的设定，WOA算法提高了收敛速度，达到全局最优。

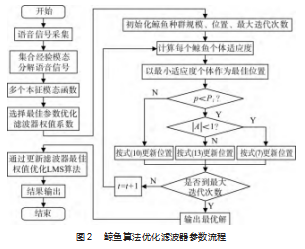
　　2改进鲸鱼算法

　　2.1集合经验模态分解（EEMD）

　　集合经验模态分解（EEMD）是Wu等[19]提出的一种将信号平稳化处理的方法，利用高斯白噪声均匀分布的特性，将其加入待处理信号中，使原始信号分解为一组平稳的信号分量，从而减弱信号波动性，该组分量称为本征模态函数（Intrinsic mode function，IMF）[20-21]。EEMD分解的主要步骤如下：

　　（4）计算各IMF分量cij(t)的平均数值，最终可得本征模态函数：

　　2.2 EEMD-WOA-LMS模型建立

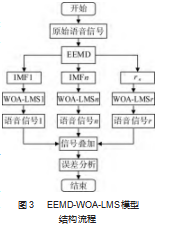
　　语音数据的非线性和波动范围大特性严重影响回声路径的估计，因此，引入EEMD方法，将非平稳语音信号进行分解，建立EEMD-WOA-LMS模型。建模步骤如图3所示。（1）对原始的语音信号进行EEMD处理，得到一组IMF分量以及1个残差分量r n(t)。（2）对每个分量分别建立WOA-LMS模型，寻优权重后得到最佳语音信号分量。（3）叠加各个语音信号分量，得到总语音信号。（4）对算法进行误差分析。

　　3仿真实验与数据分析

　　3.1语音信号预处理

　　实验采用的语音信号是在空间尺寸为5 m×5 m×3 m的真实房间测得，传声器与受话器相距4 cm。回声消除模型的放大增益G(z)=10，设置2 800个数据采样点，算法性能均在MATLAB 2022b平台上验证。

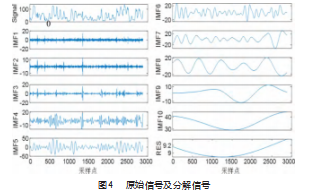
　　对采集到的语音信号进行分解处理，设定加入白噪声的幅值为0.2，最大迭代次数为100。从图4可以看出，与原始信号相比，经EEMD分解后的信号，其波动范围更平稳。

　　3.2实验结果分析

　　3.2.1算法步长对比

　　步长因子是决定自适应滤波器收敛速度快慢的重要因素，因此，图5比较了不同步长对EEMD-WOA-LMS算法的影响，实验结果可知，对于EEMD-WOA-LMS算法，其步长越小时，算法的收敛性更好且稳态误差更小。3.2.2不同信噪比下的算法性能真实场景中的声音通常是伴随着噪声的，因此为了验证不同噪声情况存在下的算法性能，实验模拟了3种真实场景中的带噪语音，在回声路径中分别添加30 dB、20 dB、10 dB信噪比的高斯白噪声。实验结果如图6~8所示。

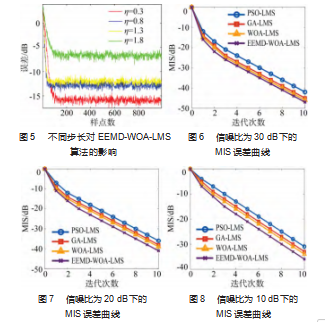
　　综合图6~8可知，改进的算法比其他算法的收敛速度更快，稳态失调更低。在信噪比为30 dB时，EEMD-WOA-LMS算法的收敛速度在其余3种算法中最快且误差最小；当信噪比为20 dB时，EEMD-WOA-LMS算法依然有更快的收敛速度；在信噪比为10 dB时，EEMD-WOA-LMS算法同样拥有最快的收敛速度，失调量比WOA-LMS算法下降了2 dB。因此，本文EEMD-WOA-LMS算法无论在大信噪比干扰还是在小信噪比干扰时，收敛速度都最快，稳态失调都最低，回声消除能力都最明显，且具有较强的鲁棒性。

　　3.2.3各算法性能对比

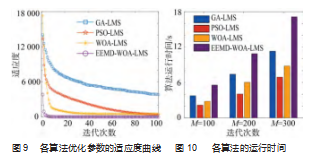
　　为验证本文所提EEMD-WOA-LMS算法的优越性，将其与PSO、GA优化算法进行了比较实验。设置初始化种群为40，迭代次数为100，4种算法的适应度曲线如图9所示。分析可知，在迭代初期，4种算法下降速度都很快，其中，EEMD-WOA-LMS算法下降速度最快，迭代次数最少，只迭代3次就达到稳态；WOA-LMS算法相对于EEMD-LMS算法收敛速度略慢，失调量略高；PSO-LMS算法虽然达到稳态时的适应度值与WOA-LMS算法相当，但其需要迭代70次左右才能达到稳态；GA-LMS算法适应度值最大，需要迭代90次左右才能达到稳定收敛。

　　为了比较算法的回声消除效果，对4种算法进行误差分析，评价回声消除效果的常用性能指标主要有3种。

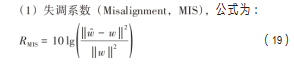
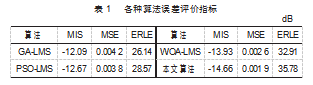
　　E为取平均操作。当RERLE越大时，说明误差信号的幅度相比于期望信号的幅度越小，回声抑制效果越好。各算法评价指标如表1所示。由表可知，EEMD-WOA-LMS算法相比于WOA-LMS算法，失调量减少了0.73 dB。本文所提算法的均方误差相比于WOA-LMS算法也有所降低。对各算法的ERLE指标排序可得，本文算法ERLE值最大，相对于WOA-LMS算法提高2.87 dB。可见，EEMD-WOA-LMS算法的回声消除能力明显较强。

　　针对数字助听器的低功耗特性，本文还从计算复杂度方面对4种算法进行分析，衡量计算复杂度的指标之一是算法从输入到输出的运行时间。图11所示为4种算法在不同迭代次数（M=100，200，300）下，实验30次后的时间。由图10可知，PSO-LMS算法时间均最短，GA-LMS算法和WOA-LMS算法的时延相当，本文所提算法在3种迭代次数下时间均略高于前3种算法，这是因为引入EEMD方法增加了算法计算量，但其结果满足助听器实时工作延时15 ms内的要求，且其收敛速度和稳态误差均优于前3种算法。

　　4结束语

　　本文提出了一种新的基于集合经验模态分解的WOA-LMS算法，并将其应用于数字助听器回声消除系统。该算法利用集合经验模态分解方法对WOA-LMS算法进行改进，研究表明：与GA、PSO算法相比，本文所采用的WOA算法收敛速度最快，实验效果最优，采用EEMD-WOA-LMS模型能更好地解决数字助听器中自适应滤波器权重设置主观性较强以及实际语音信号波动性较大的问题，与原WOA-LMS算法相比，收敛速度更快，均方误差更低，稳态失调降低了0.73 dB，ERLE值提升了2.87 dB，回声消除性能更好，验证了本文所提算法的优越性，具有很好的应用价值。

　　参考文献：

　　[1]赵力,张昕然,梁瑞宇,等.数字助听器若干关键算法研究现状综述[J].数据采集与处理,2015,30(2):252-265.

　　[2]郑洋,唐加能,柳培忠,等.数字助听器研究现状及其算法综述[J].海峡科学,2016(7):14-17.

　　[3]陈剑锋,罗伟林.基于DSP的无刷直流电动机双闭环PID伺服系统设计[J].机电工程技术,2022,51(8):96-101.

　　[4]朱紫佳.数字助听器中回声消除算法的研究[D].沈阳:沈阳工业大学,2017.

　　[5]Zhang Yuan,Xi Songtao.Application of new LMS adaptive filter-ing algorithm with variable step size in adaptive echo cancella-tion[C]//Proceedings of 2017 IEEE 17th International Confer-ence on Communication Technology(ICCT).Chengdu,China:IEEE,2017:1715-1719.

　　[6]Huang Fuyi,Zhang Jiashu,Zhang Sheng.Mean-square-devia-tion analysis of probabilistic LMS algorithm[J].Digital Signal Processing,2019,92(C):26-35.

　　[7]曾明海.基于最小均方优化算法的语音增强方法[J].焦作大学学报,2023,37(3):53-58.

　　[8]陆悠南,崔杰,肖灵.应用于助听器反馈抑制的信噪比自适应滤波算法[J].应用声学,2022,41(6):867-874.

　　[9]孙祥娥,聂冰霞.一种改进的NLMS算法用于数字助听器中的回声消除[J/OL].长江大学学报(自然科学版):1-8[2023-09-08].

　　[10]高纯,张玲华.基于L0-IPNLMS的低复杂度数字助听器回声消除算法[J].数据采集与处理,2021,36(5):939-949.

　　[11]李双.基于神经网络的数字助听器回声消除算法研究[D].成都:成都理工大学,2021.

　　[12]Xu S,He C,Yan B,et al.A multi-stage acoustic echo cancella-tion model based on adaptive filters and deep neural networks[J].Electronics,2023,12(15):3258

　　[13]赵轶骁,汪镭.基于粒子群的LMS算法在信号滤波降噪中的应用[J].微型电脑应用,2017,33(9):71-74.

　　[14]Medani K B O,Sayah S,Bekrar A.Whale optimization algo-rithm based optimal reactive power dispatch:A case study of the Algerian power system[J].Electric Power Systems Research,2018,163:696−705.

　　[15]王敏敏.面向老年人的数字助听器关键技术研究[D].合肥:合肥工业大学,2020.

　　[16]Mirjalili S,Lewis A.The whale optimization algorithm[J].Ad-vances in Engineering Software,2016,95:51–67.

　　[17]谢丽蓉,王斌,包洪印,等.基于EEMD-WOA-LMS的超短期风电功率预测[J].太阳能学报,2021,42(7):290-296.

　　[18]缪楠,张鑫,王首程,等.基于电子舌和EEMD-WOA-LMS模型的红酒贮藏年限区分[J].食品工业科技,2021,42(19):275-282.

　　[19]Wu Z,Huang N E.Ensemble eempirical mode mode decomposi-tionde composition:Anoisenoise-assisted assisted data data analysis analysis method[J].Advances in Adaptive Data Analy-sis,2009(1):1−41.

　　[20]侯春尧,毛延翩,谭大文,等.基于EEMD-SVM的混凝土大坝活动裂纹电磁辐射信号识别方法[J/OL].中国测试,1-8[2023-12-20].

　　[21]史爱武,张义欣,韩超,等.基于CEEMDAN-SE-TCN的集群资源预测研究[J].软件导刊,2023,22(4):43-47.