摘要：液体射流的破碎是一个复杂的非线性动力学问题。为研究破碎过程中气液间的动量交换机制，利用Fluent软件进行数值模拟，得到不同气流冲击液体过程中动量交换量和动量交换效率的变化规律，并进一步通过VOF to DPM模型对规律进行了验证。结果表明：在气流速度为40~90 m/s，气流密度为1.177~7.356 kg/m3的工况范围内，动量交换效率在62%~83%变化。气液之间的动量交换量随着气流速度的增大而增大，气体密度不变时，随着气流速度的增大，气液间的动量交换效率逐渐降低，最后趋于稳定；气流速度一致时，动量交换效率随气体密度的增大而减小，最后逐渐趋于稳定。在气流物性不变时，增大液体的密度和黏度均会导致气液动量交换效率的增大。将雾滴粒径分布作为液体破碎效果的计算指标，对动量交换机制进行验证，发现在气液动量交换量相等时，液体破碎后的粒径规律基本一致，最大误差为15.3%。

　　关键词：横向射流；动量交换效率；液体破碎；雾滴粒径；数值模拟

　　0引言

　　液体破碎是指液体从流道和孔径流出后经过外界气流和环境作用的扰动，由于其不稳定性产生的不稳定表面波导致液体发生断裂、拉伸、吹薄、雾化等一系列的现象[1]。这种现象被广泛研究，在食品、医药、喷嘴、航空航天、化工领域等有诸多应用[2-4]。液体横向射流破碎即液体和气流的流动方向夹角为90°时发生的气液动量交换形成的破碎现象。气液间的动量交换使液体具有强烈的扰动特性。

　　目前国内外的学者们已经针对液体横流破碎的机理和影响机制进行了深入研究。在低速横流破碎方面，张彬等[5]通过数值模拟研究了液体在横流中破碎时液膜的形态变化，并发现液体的破碎由K-H（Kelvin-Helm-holtz）和K-H（Reyleigh-Taylor）不稳定性主导。Huang等[6]发现气流温度的升高有助于减弱液体界面的扰动，使液体射流更加稳定。YU[7]等发现液体在气流中的迎风面越大，所受到的扰动越强，液体的破碎越彻底。Nam-bu等[8]针对发动机内燃料的雾化过程进行了研究，研究表明R-T不稳定性在液体射流的边缘具有主导地位。兰天等[9]进行了低速横流作用下液体的破碎实验，重点研究了不同气液量的比值对液体破碎模式的影响。在高速横流即亚音速或超音速气流破碎方面，Broumand等[10]指出横流的湍流强度是影响液体破碎模式的主要因素。Zhu等[11]研究发现速度脉冲射流可以改善射流的穿透率，

　　改善雾化性能。Hu等[12]发现在液体射流中加入高速气体射流所形成的混合射流的穿透力会明显加强。廖斌等[13]研究发现韦伯数是影响液体破碎模式的关键参数之一；Zhao等[14]分析了气流对液体破碎模式的重要影响，并发现气流的流动方式决定了液体雾化后的扩散方向。针对液体破碎的影响机制，郑勒等[15]研究了不同韦伯数下射流的撞击和破碎特性。随着韦伯数的增大，液体射流液膜也逐渐从稳定状态变为振荡波动状态，同时雷诺数的增大也会使液体破碎的雾滴颗粒粒径减小[16]。Pizziol等[17]发现射流数量的增加会使液体雾化效率降低。

　　液体横向射流破碎技术由于其结构简单，传质效率高，被广泛应用。目前针对液体射流破碎机理及影响因素均有许多研究，但是针对气液间的动量交换量及动量交换效率的大小鲜有研究。综上，本文重点针对气液间的动量交换过程，采用VOF to DPM模型和Realizable k-epsilon模型进行数值模拟，研究变密度流体在不同工况下与液体间的动量交换规律，并研究单位时间内相同动量交换量对液体破碎后颗粒粒径的影响。

　　1模型建立
      1.1物理模型

　　研究主要分两方面进行，首先进行气液间动量交换量的计算，并得到相应工况下的动量交换效率，然后观察相同动量交换量对液体破碎粒径的影响。图1所示为文中计算模型几何示意图，图中左侧蓝色入口为气流入口，右侧红色区域为气流出口区域，中间下落的绿色区域为液体表面，其中气流入口宽度与液体表面宽度相等。

　　气流与液体表面发生碰撞产生动量交换，当气动力大于液体自身的黏性力和表面张力时，液体会发生形变、拉伸、变薄、初次破碎、二次破碎和雾化等一系列过程。分别统计气流入口动量和气流出口动量的大小，二者的差值即为动量交换量，动量交换量与气流入口动量的比值即定义为动量交换效率。

　　1.2网格划分

　　在计算过程中为了保证计算结果的准确性，采用结构化网格对几何模型进行加密，如图2所示。

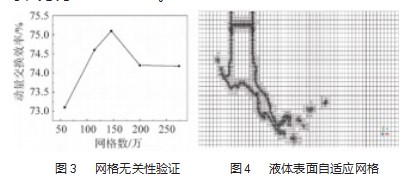
计算域尺寸为长20 mm、宽10 mm、高10 mm的立方体区域，气流入口在计算域左侧，气流入口是长为4 mm且宽为2 mm的矩形入口。对计算结果进行网格无关性验证，设置气流种类为空气，在气流速度为60 m/s时，对其进行动量交换量的计算，不断调整网格数量，发现随着网格数量的增多，网格质量的提升，气液动量交换量的值越来越趋近于稳定，网格无关性验证结果如图3所示，发现网格数较少时，综合考虑计算的时效性和准确性，最终选取网格总数量为200万，基本尺寸为0.1 mm的网格进行计算。本文进一步使用网格自适应技术进行计算，如图4所示[18]，设置加密等级为3级，网格会根据液体的流动自动对液膜表面进行加密，加密后网格最小尺寸为0.012 5 mm。

      2控制方程和参数设置
      2.1控制方程

　　利用ANSYS Fluent对该液体破碎模型进行数值模拟仿真，该模型采用连续相湍流可压缩模型进行计算，流体流动的控制方程如下。

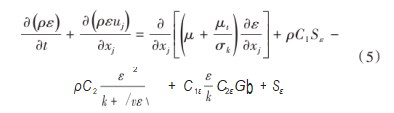
       式中：Gk和Gb为湍动能产生相；YM为湍流脉动对耗散率的贡献项；C1ε、C2ε为模型常数；σk和σε为湍流动能k和湍流耗散率ε的有效普朗特数；Sk和Sε为用户自定义的源项。

　　在液体破碎过程中，当颗粒尺寸小于网格尺寸时，VOF模型的计算会发生畸变，导致计算误差较大。为了避免这种情况，采用VOF to DPM模型将小于基本网格尺寸的液滴转化为离散液滴。在后续的计算中，还使用DPM运动方程来模拟离散液滴的飞行过程，这也便于更准确地统计颗粒的粒径、飞行速度和其他性能。渣粒的运动遵循牛顿第二定律[19]，液滴颗粒在喷射过程中遵守的动量运动方程为：

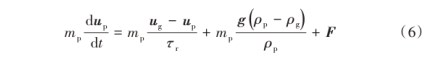
　　式中：mp为粒子质量；up为粒子相速度矢量；ug为气相速度矢量；ρp为粒子相密度；ρg为气相密度；F为其他力；τr为液滴弛豫时间。

　　2.2边界条件及模拟方案设置

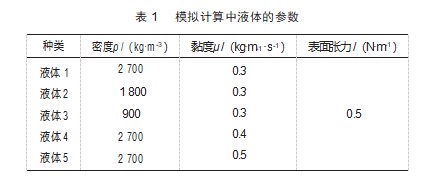
　　将图2的网格导入Fluent软件后，采用SIMPLEC的速度压力耦合求解器进行求解，选择Realizable k-epsilon作为计算的湍流模型，选择VOF to DPM模型作为研究液滴粒径分布的主要模型。气相入口条件和液相入口条件为速度入口条件，流域出口为压力出口边界条件，外部流域设置为0.1 MPa。表1所示为模拟计算中所破碎液体的物性参数。通过改变气流速度（40、50、60、70、80、90 m/s）和气流密度（1.777、1.845、3.330、5.158、7.356 kg/m3）来观测气液间的动量交换量，并统计出其动量交换效率，进一步的设置相同的气液动量交换量的算例，观测液体破碎后的粒径分布规律。

       3结果与分析

　　3.1不同气流对气液动量交换的影响

　　图5所示为横向气流破碎液体时流场的流线图，红色区域的流线速度较大，深蓝色区域的气流速度较小，黄绿色区域的气流速度介于二者之间。

由图可知，气流在破碎液体后，红色区域明显减少，气流速度降低，气体动量降低，根据动量守恒，这说明气流将一部分自身的动量传递给了液体，这部分动量称为液体破碎过程中的气液动量交换量，气液动量交换量等于气体入口的动量减去气流出口的动量值。图6所示为不同工况下气液动量交换量的大小。

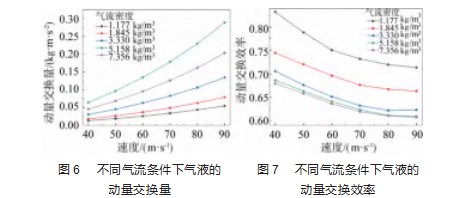
由图可知，气流的密度和速度越大，其动量交换量越大，密度越大的流体，动量交换量的增长速度越快。这说明密度和速度大的气流用来破碎液体更具优势，容易传递给液体更多的动量使其充分破碎，破碎效果更好，这个结果与Guo等[20]的结果一致。

　　如果所破碎液体的量较多，比如在钢铁工业中高炉熔渣、转炉钢渣的破碎，这些液体具有高黏性、高密度、高处理量的特点，破碎难度巨大，此时进行破碎所需的气体动量成本较大。而气体的密度、速度等均会影响其自身的动量传递效率，如何用最低的动力成本得到最佳最有效的动量交换量是需要考虑的问题。图7所示为不同气流密度和不同气流速度下气液间的动量交换效率。由图可知，对于同种流体，随着气流速度在40~90 m/s范围内增大，气液间的动量交换效率逐渐降低，气体的动量损失增大，其动量交换效率逐渐趋于稳定，最终稳定在60%~72%。此外，在气流速度一定时，增大气流的密度，发现动量交换效率逐渐降低，其降低的幅度越来越小，在气流密度为5.158、7.356 kg/m3时，二者的动量交换效率已经非常接近。
      3.2不同液体对气液动量交换的影响

　　在图5中可以观察到在液体破碎过程中，并非所有气流都可以打击到液体表面进行动量交换，一部分气流作用与液体表面，有一部分气流从破碎液体中间的缝隙穿过，还有一部分气流因为液体过早破碎导致未能接触到液体直接向出口流去。因此，液体的性质同样对气液动量交换有着重要的影响。

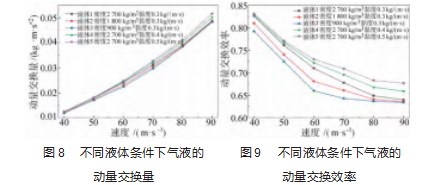
　　图8所示为气体密度保持1.177 kg/m3不变时，表1中各种液体性质变化对气液动量交换量的影响。由图可知，整体上动量交换量随气流速度增大而增大，针对所破碎液体的不同，动量交换量的数值差别较小，但也明显具有一定规律。液体的密度和黏性均会对动量交换量有一定的影响，液体密度和黏性越大，动量的交换量越多，这是因为液体密度和黏性增大均会引起液体惯性力和黏性力的增加，使液体的破碎难度增大，液体不易发生断裂，气流从液体内部穿过的现象降低，因此动量交换量增大。且在气流速度为90 m/s时，可以发现密度变化所引起的动量交换量的变化要高于液体黏性变化的结果。

　　图9所示为各种液体条件下气液破碎的动量交换效率的变化，液体黏性的变化规律基本与图7结果规律一致。可以发现液体密度的大幅度降低会引起动量交换效率有较明显的下降，液体黏性的改变对动量交换效率也具有一定的影响，但是所引起的动量交换效率的变化幅度较小。图9中动量交换效率的曲线不够平滑，波动值较大，这可能是由于高黏度高密度的气液流体破碎过程对于计算模型的湍流模型和网格要求都比较高，造成的误差较大。

      3.3动量交换量对液体破碎的影响

　　液体在横向气流作用下破碎过程的原理本身是属于气液动量的交换过程。液体在破碎过程中受到内力和外力的共同作用，其所受外力主要包括气体的气动力、液体所受的重力等因素，其所受的内力主要包含其自身黏性力和表面张力等因素。外力具有促使液体表面液膜发生形变的作用，而内力具有阻碍液体发生形变的作用，当液体所受外力大于液体自身内力时，液体就会发生破碎。在液体所受外力大于内力的条件下，气液之间的动量交换量即为衡量液体破碎效果的影响因素。下面将通过数值模拟计算验证这一结果。

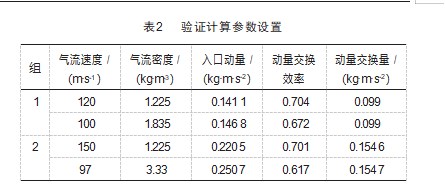
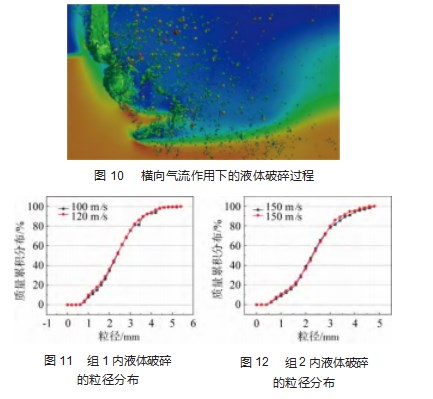
　　液体破碎后的颗粒粒径分布是衡量液体破碎效果的重要指标。因此通过按照表2中的结果参数进行验证计算。计算共分2组结果进行验证，通过设置各组气流的物性参数，使组内的2种气流与液体间的动量交换量相等，然后观察液体破碎后液滴颗粒的粒径分布结果。图10所示为利用VOF to DPM模型进行液体在横向气流作用下的破碎过程的模拟计算，液体经过气流的打击最终撕裂为小液滴颗粒。通过对表3中的工况进行模拟计算，最终得到了如图11和图12所示的在对应粒径范围的颗粒质量累积分布对比。由图可知，组1和组2内的2种气流破碎同一种液体时所得到的粒径分布结果误差较小，最大误差为15.3%，计算结果的粒径分布规律基本保持一致，因此可以进一步说明，在液体所受外力大于内力时，保证气液之间的动量交换量是影响液体破碎的主要影响因素。

      4结束语

　　本文针对液体在横流作用下的破碎过程，对气液之间的动量交换机制进行了数值模拟研究，重点分析了气液物性对动量交换机制的影响，包括气流速度、密度、液体密度、液体黏性等参数，并通过数值模拟进行了验证，主要得出以下结论。

　　（1）在气液物性一定时，气液之间的动量交换量随着气流速度的增大而增大。

　　（2）气体密度不变时，随着气流速度的增大，气液间的动量交换效率逐渐降低，最后趋于稳定。气流速度一致时，动量交换效率随气体密度的增大而减小。随着气流密度的不断增大，动量交换效率逐渐趋于稳定。
       （3）在气流物性不变时，增大液体的密度和黏度均会导致气液动量交换效率的增大。

　　（4）当液体所受外力大于内力时，液体会发生破碎，此时气液间的动量交换量是衡量液体破碎效果的主要影响因素，气液间动量交换量大小一致时，改变气流种类，液体的粒径分布规律基本维持不变。

      参考文献：

　　[1]李帅兵,司廷.射流破碎的线性不稳定性分析方法[J].空气动力学学报,2019,37(3):356-372.

　　[2]司廷,李广滨,尹协振.流动聚焦及射流不稳定性[J].力学进展,2017,47:178-226.

　　[3]张冲,焦光伟,祝韬,等.圆锥长直管段喷嘴内流场仿真研究[J].重庆理工大学学报(自然科学),2017,31(12):105-110.

　　[4]张嘉丽,李浩,梁文宏.基于FLUENT的高压精细雾化喷嘴特性研究[J].机电工程技术,2023,52(2):63-67.

　　[5]张彬,成鹏,李清廉,等.液体横向射流在气膜作用下的破碎过程[J].物理学报,2021,70(5):230-241.

　　[6]HUANG J K,ZHAO X.Numerical simulations of atomization and evaporation in liquid jet flows[J].International Journal of Multiphase Flow,2019,119:180-193.

　　[7]YU S H,YIN B F,BI Q S,et al.The influence of elliptical and circular orifices on the transverse jet characteristics at superson-ic crossflow[J].Acta Astronautica,2021,185:124-131.

　　[8]NAMBU T,MIZOBUCHI Y.Detailed numerical simulation of primary atomization by crossflow under gas turbine engine com-bustor conditions[J].Proceedings of the Combustion Institute,2021,38(2):3213-3221.

　　[9]兰天,孔令真,陈家庆,等.低速横流作用下液体射流初次破碎实验[J].化工进展,2020,39(4):1282-1291.

　　[10]BROUMAND M,AHMED M M A,BIROUK M.Experimental investigation of spray characteristics of a liquid jet in a turbu-lent subsonic gaseous crossflow[J].Proceedings of the Combus-tion Institute,2019,37(3):3237-3244.

　　[11]ZHU Y H,XIAO F,LI Q L,et al.LES of primary breakup of pulsed liquid jet in supersonic crossflow[J].Acta Astronautica,2019,154:119-132.

　　[12]HU R S,LI Q L,LI C,et al.Effects of an accompanied gas jeton transverse liquid injection in a supersonic crossflow[J].Acta Astronautica,2019,159:440-451.

　　[13]廖斌,张桂夫,王鲁海,等.冲击作用下液滴在环境液体中的变形破碎行为[J].实验流体力学,2016,30(5):9-16.

　　[14]ZHAO J F,REN Y J,TONG Y H,et al.Atomization of a liquid jet in supersonic crossflow in a combustion chamber with an ex-panded section[J].Acta Astronautica,2021,180:35-45.

　　[15]郑勒,白富强,杨子明,等.不同环境压力下幂律流体撞击射流破碎特性[J].内燃机学报,2019,37(1):76-83.

　　[16]KASHANJ S,KEBRIAEE A.The effects of different jet veloci-ties and axial misalignment on the liquid sheet of two colliding jets[J].Chemical Engineering Science,2019,206:235-248.

　　[17]PIZZIOL B,COSTA M,PANÃO M O,et al.Multiple impinging jet air-assisted atomization[J].Experimental Thermal and Fluid Science,2018,96:303-310.

　　[18]LIU X H,WEN Z,DU Y H,et al.Numerical simulation of the slag granulation processin gas quenching under multi-influenc-ing factors[J].Iranian Journal of Science and Technology,Trans-actions of Mechanical Engineering,2023,47(4):1733-1745.

　　[19]ZHANG Y,XU J,CHANG Q,et al.Bi-layer coarse-grained DPM of gas-solid systems with mesoscale heterogeneity re-solved[J].Chemical Engineering Science,2022,263:118058.

　　[20]GUO J P,WANG Y B,BAI F Q,et al.Unstable breakup of a power-law liquid fuel jet in the presence of a gas crossflow[J].Fuel,2020,263:116606.