摘要：蚁群算法所具备的合作搜索能力被广泛用于寻找单台AGV最短路径，却不适用解决现实情况中多台AGV同时使用的问题，为此提出了融合任务规则优先级的蚁群算法实现多AGV路径规划，用于解决现实问题中多台AGV同时使用而且存在多种碰撞冲突的情形。通过将AGV运行的路径环境进行建模等针对性措施，把蚁群算法引入到AGV路径规划的现实问题中，然后考虑多AGV路径规划可能存在的不同碰撞冲突类型，并考虑不同AGV拥有不同的任务优先级的现实情况，提出了避免AGV碰撞的策略，形成了基于融合任务规则优先级蚁群算法的多AGV路径规划算法。通过仿真实验结果，证实所提出的算法可以避免多台AGV之间的路径冲突，同时利用了蚁群算法寻求最优路径的能力，改进后的蚁群算法能够用于多AGV路径规划的实际场景中。

　　关键词：多AGV路径规划，蚁群算法，任务优先级，最优路径，避碰策略，AGV导航，AGV调度

　　0引言

　　自动导航车[1]（Automated Guided Vehicles，AGV）是一种安装了自动引导系统，不需要人工指引航向就可以沿着预先设定好的运行线路端点进行自动行驶的搬运车，实际应用中主要用于制造工厂里运送物料等。AGV的导航方式有以下几种类型：铁磁陀螺惯性引导式、电磁感应引导式、激光引导式、视觉引导式等，可以据此将AGV进行分类[2]。

　　路径规划是AGV的主要功能之一，对AGV应用起着至关重要的作用，是实现AGV自主导航的关键技术。目前，国内外学者对AGV路径规划问题进行了大量研究。Li等[3]提出一种基于生长的显示拓扑优化方法，用于在充满障碍物的复杂环境中为机器人规划最优路径。Lami‐ni C等[4]提出一种改进的适应度函数，用于全局环境下的路径规划。针对传统蚁群算法在进行路径规划时存在搜索效率低、容易陷入局部极值等问题，王晓燕等[5]针对上述问题提出改进势场蚁群算法，利用人工势场法构造启发式函数，提出初始信息素不均等分配原则，并利用仿真实验验证了改进算法在解决搜索效率低、局部极值问题上的有效性。

　　上述路径规划大都针对某类特定场景，虽取得一定成果，但面对的多是单个AGV的最佳路径规划，对于多AGV的复杂多变的工况环境，通常是以牺牲运输效率和路径安全为代价。

　　基于以上原因，为了寻求高效、安全，适用复杂工况环境的AGV路径规划策略，本文提出基于融合任务规则优先级的蚁群算法实现多AGV路径规划。算法的目标是即可以利用蚁群算法寻求单台AGV最优路径的能力，又综合考虑了如何避免多台AGV之间路径冲突的情形，从而能够将蚁群算法用于多AGV路径规划的实际场景中。

　　1蚁群算法

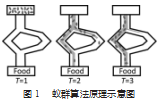
　　生物学研究发现：单只蚂蚁无法找到蚁穴和食物之间的最短路径，而一群相互协作的蚂蚁却能够做到，原因在于蚂蚁个体之间的行为可以相互作用[6]。每只蚂蚁在它所爬行的路径上留下一种被称为信息素的物质，是用作蚂蚁个体之间进行信息交流和传递的载体，蚂蚁正是靠这种信息素彼此影响。

　　蚁群算法是受到大自然中蚂蚁群觅食行为的启发而提出的，作为一种仿生学算法，它模拟了自然界中的蚂蚁群行为。每只蚂蚁在它经过的路径上释放信息素，同时，路径上信息素浓度的大小也影响蚂蚁选择路径。

　　初始情况下，蚂蚁选择不同路径的概率是等同的，因为蚂蚁的爬行速度相同，分布的间距也就相同，这样会导致越短的路径上聚集的蚂蚁密度越大，信息素浓度也越大[7]。随着时间推移，较短路径上的蚂蚁继续增多，信息素浓度也相应增多，后续蚂蚁选择较短路径的概率就越变越大，如此就形成了一种正反馈，最终整个蚁群将找到一条最短路径或者叫做最佳路径。这个过程中的原理如图1所示。

　　从深层意义上来理解，蚁群算法是一种属于人工群集智能领域的优化算法，它具有独特的强有力的合作搜索能力。

　　2 AGV路径规划

　　如果把每一个AGV对照于自然界中的一只蚂蚁，那么使用蚁群算法进行AGV路径规划就可以使AGV获得最优路径。不同的是，并不需要运行每一个AGV实体才能获得最优路径，可以使用仿真计算的方法得到AGV在每一个起始点到目标点之间的最优路径，实体AGV只需要在真实运行的过程中按照这些计算好的最优路径运行即可。

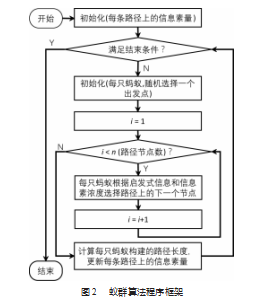
　　将蚁群算法用于AGV路径规划需要对环境进行建模，以便于AGV的运行环境能够被数学抽象和使用算法进行度量。除此之外，需要针对AGV进行蚁群算法的实现，以及路径规划问题。蚁群算法的程序框架如图2所示。群蚁算法的2个核心步骤是路径节点的概率选择和信息素更新。

　　2.1环境建模

　　环境地图的建立是AGV路径规划的核心部分之一，利用栅格法为AGV构建一个带有障碍物的工作环境。这其实是基于以下两点假设：（1）假设AGV的工作环境是一个二维空间，其中AGV被视为以固定速度移动的一个质点；（2）障碍物如果未占满一个栅格，按一个栅格处理。这样，整个工作空间被划分为两部分：可行区域χf和不可行区域χ0，其中AGV可以在可行区域内自由移动，障碍物位于不可行区域。在整个网格环境中，网格按照从左到右、从上到下的顺序进行编号，建立网络编号和坐标如下的映射关系：

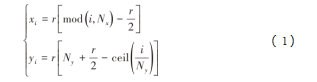
　　式中：r为每个单元网格的大小；i为网格的编号；Nx为每一行网格的数目；Ny为每一列网格的数目；mod为求余运算；ceil为向上取整。

　　通过以上公式进行建模，得到的环境地图模型如图3所示。

　　2.2路径节点的概率选择

　　蚁群算法中的每个蚂蚁个体都保存一个路径向量，用于存放自身依次经过的路径节点。蚂蚁在每一个路径节点按照随机概率选择下一个路径节点，随机概率按照以下公式计算式中：

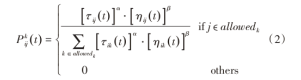
i、j分别为起点和终点；ηij为能见度，是两点i、j之间距离dij为的倒数；τij(t)为时间t时，由i到j的信息素强度；allowedk为尚未访问过的节点集合；α为信息素权重，权重越大，则蚂蚁选择走过这条路径的概率越大；β为启发因子，反映启发式信息在指导蚁群搜索过程中的相对重要程度。

　　2.3信息素更新

　　在初始化结束后，算法会给每条路径生成一个初始的信息素浓度值。每一次迭代结束，对所有蚂蚁走过的路径进行计算，并更新相应路径上的信息素浓度[8]。经过反复迭代，最短路径上的信息素浓度最高，从而被选择为最优解或者称为最优路径。

　　除了上述的信息素释放过程，与此同时，每一次迭代计算，所有路径上的信息素都有一个挥发过程。

　　所以，新的信息素浓度总值=挥发后剩余的信息素+蚂蚁经过后留下的新信息素。公式如下：

　　3多AGV路径规划
       3.1规划策略

　　多AGV协同作业时，首当其冲需要考虑的是多AGV的路径规划问题，也就是最优的多AGV无碰撞策略。目前主要有4类针对多AGV路径规划的策略：基于图的方法、基于采样的方法、基于模型的方法、基于智能算法的方法[9]。

　　（1）基于图的方法

　　Dijkstra算法作为一种广度优先搜索方法，基本思想是从标号为0的初始节点开始搜索，遍历所有相邻节点以寻找权重最小的边，重复上述过程，同时比较权重并存储最优路径的权重，直至搜索到目标点，整个搜索过程结束。文献[10]使用Dijkstra算法从三角分解图中获取一条最优无碰撞路径，采用遗传算法对规划得到的路径平滑处理。

　　文献[11]提出一种基于图的AGV路径规划算法，采用Floyd算法对不同路径赋权。首先从多AGV协作、环境信息等方面介绍多AGV路径规划算法；其次通过对Floyd算法进行编码，建立深度图模型，对AGV路径进行优化。

　　（2）基于采样的方法

　　对环境中的障碍物进行碰撞检测，从而快速获得可行路径，这就是基于采样的路径规划算法的原理。

　　（3）基于模型的方法

　　基于模型方法的基本思想是建立AGV的运动学与动力学模型，通过等式或不等式约束来求解智能体路径规划问题。针对基于模型方法存在计算成本高的问题，Song等[12]提出一种混合整数线性规划方法，该方法能够保证多个AGV同时进行配送任务。

　　（4）基于智能算法的方法

　　近年来，许多研究人员从不同生物的生物学行为中获得启发，开发出基于智能算法的方法。基于智能算法的方法主要通过模拟自然界中生物行为，从生物行为中抽象出基本模型来处理多AGV路径规划问题。文献[13]提出一种新颖的动态分布式粒子群优化算法，用于多AGV的路径规划，该方法通过增加种群的多样性来避免算法停滞和局部最优问题，提高了收敛速度，能够为环境中的AGV找到无碰撞的最优路径。文献[14]提出一种基于优先级的混合集中和分布式算法，采用基于优先级的方法为每个AGV提供优先级，从而在发生冲突情况下绕过其余AGV，该算法提高了多AGV路径规划问题的有效性和高效性。

　　3.2规划实现

　　在实际装配运输过程中，多数场景不仅仅是一台AGV在运行，而是多台AGV同时运行。企业制造执行系统（Manufacturing Execution System，MES）与AGV调度系统（Scheduling System）进行通信，由MES向调度系统发送搬运任务的请求，由调度系统指定车间中空闲的AGV执行搬运任务。

　　在执行运输任务的过程中，定义AGV1和AGV2发生

　　路径冲突的条件：AGV1对应的坐标pi(t)为(xi(t),yi(t))，AGV2对应的坐标pj(t)为xj(t),yj(t)，两辆AGV之间的距离d(pi(t),pj(t))可表示如下：

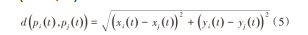
　　工作环境行驶过程中会发生碰撞，ΔLsafe为AGV之间发生碰撞的安全距离。

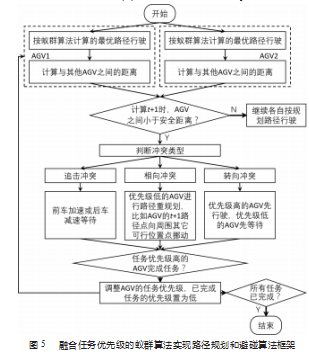
　　根据具体情况，两台或多台AGV之间又可能发生以下3种类型的路径冲突：追击冲突、相向冲突、转向冲突[15]。

　　追击冲突是指两辆AGV沿着同一车道朝着相同方向行驶，后车的速度大于前车的运行速度，经过一段时间，后车将追上前车，最终导致两辆车发生碰撞。

　　相向冲突是指AGV1和AGV2在同一车道上朝着对方行驶，如果不采取相应措施干预，经过一段时间后，两车将产生相向冲突而发生碰撞。

　　转向冲突一般发生在路径的岔道口位置，根据路径规划算法规划好的路线，经过一段时间，AGV1和AGV2将到达同一位置点。若在此过程中不对AGV速度或路线进行调整，AGV1和AGV2将发生转向冲突，容易发生碰撞。这3种类型的碰撞示意图如图4所示。

　　对于3种冲突类型，可以设置不同的避碰策略。（1）对于追击冲突，当位于前方的AGV2检测到位于后方的AGV1到自身的距离小于安全距离时，AGV2可以加速行驶，或者让AGV1减速甚至停下，直到AGV1和AGV2之间的距离大于安全距离，则两台AGV恢复到原来的速度继续行驶。（2）对于相向冲突，针对优先级不同的两辆AGV，算法倾向于让优先级较低的AGV进行路径的重新规划，比如，让优先级低的AGV的t+1路径点向周围其他可行位置点挪动，而不是继续在原路径上走到下一个规划点。重规划完成后，低优先级的AGV按照新规划好的路径行驶，高优先级的AGV则继续按照原先规划的路径行驶。（3）对于转向冲突，按照分配的优先级原则，优先级大的AGV先行驶，优先级小的AGV先等待，当两车之间的距离大于安全距离后，优先级小的AGV再行驶。

　　以上结合了蚁群算法以及任务规则优先级的路径规划和避碰策略可以用图5所示算法框架表示。

　　4仿真实验分析

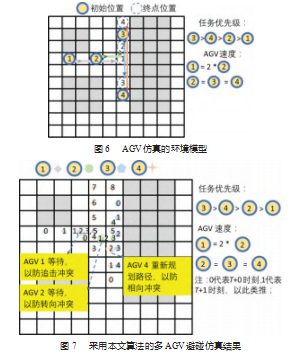
　　仿真采用10×10的栅格划分环境模型，4台AGV的初始点和目标位置各不相同，如图6所示。利用前述的蚁群算法规划得到各台AGV的路径，这里主要结合任务优先级，利用本文提出的融合任务规则优先级的蚁群算法对多AGV路径规划中的避碰进行模拟仿真。

　　5结束语

　　本文针对实际装配运输过程中的多AGV路径规划问题，提出基于融合任务规则优先级的蚁群算法实现多AGV路径规划，并对算法进行了仿真实验。传统蚁群算法具有的合作搜索能力的特点，能够计算出任意一个初始点到终点的最优路径，但比较适合用于指导单台AGV进行最优路径规划。而实际运输场景中，往往是多台AGV同时作业，且每台AGV的任务有不同的优先级。本文基于蚁群算法，针对多台AGV的场景增加了任务优先级的考虑和避碰策略，避免多台AGV之间的路径冲突，同时又利用了蚁群算法寻求最优路径的能力，使蚁群算法能够用于多AGV路径规划的实际场景中。

　　参考文献：

　　[1]姚佳杰.基于视觉的AGV道路识别和导引[D].杭州:浙江大学,2014.

　　[2]崔丽丽,万翟.安全性与自动化并举——激光光电传感器在AGV上的应用[J].现代制造,2005(6):62-64.

　　[3]Li B,Liu H,Su W.Topology optimization techniques for mobile ro‐bot path planning[J].Applied Soft Computing,2019,78(3):528-544.

　　[4]Lamini C,Benhlima S,Elbekri A.Genetic algorithm based ap‐proach for autonomous mobile robot path planning[J].Procedia Computer Science,2018,127(12):180-189.

　　[5]王晓燕,杨乐,张宇.基于改进势场蚁群算法的机器人路径规划[J].控制与决策,2018,33(10):1775-1781.

　　[6]杨丽.云南YH股份物流配送网络优化研究[D].昆明:云南财经大学,2014.

　　[7]郑娟毅,付姣姣,程秀琦.面向物流车辆路径规划的自适应蚁群算法[J].计算机仿真,2021,38(4):477-482.

　　[8]蒋励菁.无线通信网络中若干智能化技术研究[D].南京:南京邮电大学,2019.

　　[9]廖凯文.多AGV路径规划优化算法及调度系统的研究[D].合肥:合肥工业大学,2020.

　　[10]Mac T T,Copot C,Tran D T,et al.A hierarchical global path plan‐ning approach for mobile robots based on multi-objective parti‐cle swarm optimization[J].Applied Soft Computing,2017,59(2):68-76.

　　[11]Lyu D,Chen Z,Cai Z,et al.Robot path planning by leveraging the graph-encoded Floyd algorithm[J].Future Generation Computer Systems,2021,122(7):204-208.

　　[12]Song B D,Kim J,Morrison J R.Rolling Horizon Path Planning of an Autonomous System of UAVs for Persistent Cooperative Service:MILP Formulation and Efficient Heuristics[J].Journal of Intelligent&Robotic Systems,2016,84(1):241-258.

　　[13]Ayari A,Bouamama S.A new multiple robot path planning algo‐rithm:dynamic distributed particle swarm optimization[J].Ro‐botics and biomimetics,2017,4(1):8-14.

　　[14]Dewangan R K,Shukla A,Godfrey W W.A solution for priority-based multi-robot path planning problem with obstacles using ant lion optimization[J].Modern Physics Letters B,2020,34(13):564-560.

　　[15]杨康.基于改进蚁群算法的汽车装配车间AGV路径规划策略研究[D].长春:长春工业大学,2022.