摘要：水轮发电机轴承在运行时承受着整体机组的轴向负荷与复杂水推力，针对其产生的非稳态、非线性特征的振动信号，提出一种基于Hilbert包络谱分析与遗传算法支持向量机（GA-SVM）相结合的诊断方法，用于轴承故障状态的识别。首先对推力轴承运行时产生的振动信号进行集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD），分解成若干个固有模态函数（Intrinsic Mode Function，IMF），依据峭度准则选取主要IMF分量并通过Hilbert包络谱分析，计算包络谱熵，将归一化后的包络谱熵作为特征向量输入GA-SVM进行训练与故障识别。仿真实验结果表明，基于EEMD包络谱熵分析法相比于时频域图像处理能更好地提取出复杂工况下的故障信号特征，遗传算法支持向量机识别准确率达96.87％，该算法模型可进一步应用于水轮发电机轴承故障诊断。

　　关键词：水轮发电机，轴承故障诊断，集合经验模态分解，Hilbert包络谱熵，遗传算法支持向量机

　　0引言

　　作为水电站生产电能的主要装置，水轮发电机是指通过水轮机将水能转化为电能的动力设备，其内部的推力轴承对整体机组的正常运行具有重要作用[1]。当水轮发电机与机组内旋转部件包括发电机转子、水轮机转轮同步运行时，轴承不仅支撑整体机组的轴向负荷，还传递各部件重量至荷重机架，再经过荷重机架传送至混凝土基础上；同时由于大多数水电站所处流域水况复杂，水轮发电机各部件会受到水流的高速冲刷与磨损，由水压力推动水轮机转轮叶片形成的轴向水推力将直接作用于轴承上，进而导致机组发生振动。作为重要的支撑部件，轴承一旦振动严重超过范围值而受力不平衡、油膜破坏甚至发生烧损故障，将在很大程度上影响到水轮发电机组的安全运行。因此，实际复杂工况与负载下轴承所产生的振动信号，其非稳态、非线性与强噪声特征会愈发明显，如何从多种影响因素下有效提取出振动信号的故障特征向量来识别轴承故障位置及受损程度，成为当前轴承故障诊断工作中的重点与难点，对实现“预知维修”，避免机械设备进一步加重破坏具有非常重要的意义[2]。

　　针对故障信号非稳态、非线性、强噪声与频谱复杂等特征，若直接将原始振动信号进行时域或频域单方面分析，其高频、模态混叠特性会对诊断结果造成极大误差。程军圣等[3]将经验模态分解（Empirical Mode Decom‐position，EMD）和AR模型相结合，通过EMD分解[4]信号并提取自回归参数和残差的方差，形成特征向量输入支持向量机进行诊断分类，具有良好的局部瞬时特征表征能力，但EMD分解出的IMF分量往往存在端点效应和模态混叠现象[5-6]，难以提取到原始信号的真实特征。Wu和Huang等[7]针对原始EMD算法出现的问题，提出集合经验模态分解（EEMD），通过添加高斯白噪声的方法以消除模态混叠现象带来的影响[8-9]。运用Hilbert变换[10]可以对IMF分量进行信号解析，但仍存在结构复杂与计算量大的问题。因此本文采用EEMD-Hilbert包络谱分析，并结合信息熵[11]，在改善信号模态混叠现象的同时，形成的包络谱熵能够度量包络信号频率分布的均匀程度，有效处理非平稳、非线性信号。

　　支持向量机（SVM）[12-13]是一种对信号数据进行二元分类的广义线性分类器，其分类参数的设置很大程度影响着识别精度与诊断效果。目前，改进模型所使用的优化算法例如人工蜂群算法（Artificial Bee Colony Algo‐rithm，ABC）[14]、粒子群算法（Particle Swarm Optimiza‐tion，PSO）与BP神经网络等仍存在收敛速度慢、容易陷入局部最优和过拟合等缺点[15-16]，利用遗传算法[17]优化支持向量机，其搜索能力强，变异机制可避免算法陷入局部最优。基于上述分析，本文提出采用EEMD分解出反映振动信号局部特性的IMF分量，经过峭度值筛选与Hilbert变换计算出包络谱熵值，归一化形成特征向量，最后导入GA-SVM进行样本训练与测试，实现精准的轴承故障识别与诊断。

　　1数据特征提取

　　1.1集合经验模态分解原理

　　根据高斯白噪声频谱均匀分布的统计特性，EEMD[18]是在经验模态分解的基础上给目标信号加入多次高斯白噪声，使分解出的信号在不同尺度上具有连续性，从而有效改善模态混叠现象。EEMD适用于不同工况下非线性与非稳态信号，具体分解步骤如下。

　　步骤1：随机生成均值μ=0，标准差σ为常数的高斯白噪声ni(t)，并将白噪声ni(t)加到原始信号x(t)上，形成一个新的信号xi(t)，即xi(t)=x(t)+ni(t)（1）式中：t为时间；设定总体平均次数N，也表示EMD分解次数；i表示第i次分解，i=1，2，…，N。

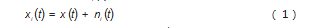
　　步骤2：对含有噪声信号xi(t)分别进行EMD分解，得到一系列IMF分量和的形式：

　　式中：J为IMF个数；ci,j(t)为第i次进行EMD分解后得到的第j个IMF分量，依照频率从高到低排列；ri(t)为第i次分解后得到的残余分量，代表信号的平均趋势。

　　步骤3：若i<N，则对步骤1和步骤2循环执行，i=i+1；当i≥N时，停止EMD分解；每次加入白噪声所分解得到IMF集合为：c 1,j(t)，c2,j(t)，…，cN,j(t)，j=1，2，…，J。

　　步骤4：根据不相关序列的统计平均值为零的原理，对上述分解得到的IMF分量进行总体平均运算，以消除多次加入高斯白噪声对真实IMF的影响；最终EEMD分解得到的IMF分量与最终残差r(t)表示为：

　　1.2 IMF分量筛选

　　峭度系数K是反映随机变量分布特性的数值统计量[19]，也是四阶中心矩。由于当信号中存在瞬时冲击特征时会显得非常敏感，因此常应用于对轴承故障信号的处理与特征提取。峭度的数学公式描述为：

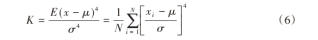
　　式中：K为信号x(t)的峭度值；xi为振动信号序列；μ为信号的均值；σ为信号的标准差；N为信号的长度。

　　峭度是描述波形尖峰度的无量纲参数，与轴承转速、尺寸等因素无关。当轴承正常工作时，所测振动信号幅值趋于正态分布，峭度指标值K≈3，即IMF分量的峭度值与波动区间较小；当轴承出现故障时，冲击特征明显，信号幅值偏离正态分布，含有故障信号的IMF分量峭度值与波动区间增大。因此，IMF分量峭度值越大，表明冲击成分越明显，故障特征越容易提取，设定阈值为3，将峭度值大于3的IMF分量作为主要分量。

　　1.3基于Hilbert变换的包络谱熵

　　当水轮发电机推力轴承发生故障时，运转中会发生周期性冲击，进而产生复杂且非稳态的振动信号。采用EEMD分解信号后得到的IMF分量比EMD分解后的IMF分量保留了更多的频率信息，且IMF分量是调制信号，其包络更集中包含了故障信息，因此采用Hilbert变换计算包络谱，并利用包络谱特征对IMF分量进行谱分析可有效反映冲击成分对频率分布带来的变化，效果也更为直观；若直接运用Hilbert包络谱作为特征输入分类器，会由于特征频点过多而使结构复杂化，增大计算量。因此引入信息熵的概念来衡量轴承故障信号的信息含量，有效提取故障分类特征。

　　信息熵作为一个系统信息含量的量化指标[20]，可在信源整体上度量输出信息的不确定性，也可以进一步用来作为系统方程优化的目标或参数选择的判据。信息熵值大小与系统变量分布不确定性程度有关，秩序越乱，变量分布不确定性越大，信息熵值就越大。设一个离散随机变量X={x1，x2，…，xn}为信源，每一个变量X所出现的概率为P（xi）=Pi，则变量X的信息熵可表示为：

　　包络谱熵是指在包络谱的基础上，结合信息熵的定义而提出的一种可以衡量信号在包络域内频率分布均匀程度的指标，作为判断是否为故障包络谱的依据。因此本文提出先对筛选后的主要IMF分量进行Hilbert变换获取包络谱，再进一步计算包络谱熵并进行归一化，将熵值作为特征向量输入支持向量机进行训练与测试，完成故障识别，该方法步骤如下。

　　（1）对主要IMF分量进行Hilbert变换，公式如下：

　　式中：Pi为包络谱内第i个点的谱值在整体中的所占比，i=1，2，…，n；n为包络谱点的个数。

　　2 GA-SVM模型建立与故障识别
       2.1支持向量机

　　支持向量机既是统计学习理论的基础部分，也是一种应用于模式分类识别的分类算法，具有较高的准确性。SVM的基本思想可以表示为通过核函数对训练样本进行升维处理，映射转化到高维特征空间，并在空间内建立最优分类超平面。基本思想如图1所示，三角形和圆形分别代表两类样本，H是最优分类线，H1、H2是两条平行于分类线且分别穿过两类距离H最近样本的直线，两线之间的距离为分类间隔d1，H1、H2穿过的两类样本称为支持向量。

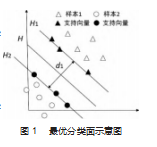
　　假设训练样本的数据集合为：D={（xi，yi）|i=1，2，…，n}，其中xiεRd，yiε{1，-1}，n表示样本数，d表示空间维数。

　　式中：w为权值向量；x为输入向量；b为偏置系数；n为向量的个数。

　　为更好寻求最优分类面，可转化为二次规划问题进行求解，xi为非负松弛变量，C为惩罚因子，函数与约束条件如下：

　　针对非线性问题处理的关键，在于通过将数据映射到高维特征空间，根据Mercer定理采用合适的核函数K（xi，xj）来实现非线性分类，并引入拉格朗日系数ai，最后得到的最优分类超平面函数表示为：

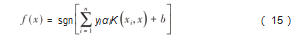
　　在构建支持向量机做分类识别时，其分类性能的高低在于惩罚因子C与核函数参数g的选取，只有优化SVM参数值，才能更好提高分类准确率。

　　2.2 GA-SVM模型

　　遗传算法（GA）是一种通过模拟自然进化过程进行全局搜索最优解的方法，利用GA对SVM进行分类参数优化，有利于改善故障诊断效果。主要步骤如下：（1）选择RBF核函数并对惩罚因子C与核函数参数g进行编码，生成一个初始化种群；（2）用样本对SVM进行训练，计算分类准确度；（3）计算种群中个体的适应度值，得到适应度函数；（4）判断是否满足GA终止条件，若满足，则进行解码、获取优化参数C和g，当达到分类准确度要求后，输出分类结果；（5）若不满足，则进行选择、交叉和变异的遗传算子操作，经过迭代计算生成新的种群，并返回第步骤（2）开始新循环。

　　2.3基于EEMD-Hilbert和GA-SVM的轴承故障诊断

　　基于EEMD-Hilbert的信号特征提取和GA-SVM故障诊断流程如图2所示，具体步骤：（1）信号获取：在运行设备上检测与提取出原始振动信号，并对数据样本分组；（2）EEMD分解：采用EEMD对数据样本进行分解，根据峭度准则筛选出主要IMF分量；（3）包络谱分析：对选取的IMF进行Hilbert包络谱分析，计算包络谱熵值后归一化，构成特征向量输入SVM；（4）GA优化SVM：将训练样本代入GA-SVM进行训练，得到最优SVM分类参数；（5）模式识别：将训练好的GA-SVM模型进行测试，并通过实验信号数据完成故障分类。

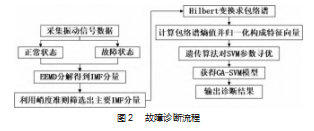
　　3实验分析

　　3.1信号EEMD分解与峭度值计算

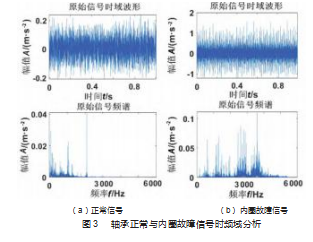
　　为后期将理论方法更好地运用于水轮发电机现场轴承测试实验，本文采用美国凯斯西储大学电气工程实验室公开轴承数据库对上述方法进行仿真实验验证，轴承试验台采用传感器对电机驱动端轴承进行数据采集，选取滚动轴承在采样频率为12 kHz，转速为1 797 r/min运行情况下正常工作、内圈故障、外圈故障以及滚动体故障4种不同状态的振动信号数据，每种状态均分32组数据样本并随机抽取各16组数据作为训练样本，余下16组作为测试样本。由图3可知，以该轴承的正常信号与内圈故障信号为例进行时频域分析，内圈故障信号相较于正常信号存在更加明显的振动冲击特征，可提取出更多的频率信息。故将内圈故障信号进行EEMD分解，所得IMF分量反映了从高频到低频不同频率分量的信息特征，如图4所示。将分解后的IMF分量结合峭度准则计算其每个峭度值后，可知前4个IMF分量与原信号相关度较大，峭度值计算结果如表1所示。

　　3.2 IMF分量的包络谱熵特征向量提取

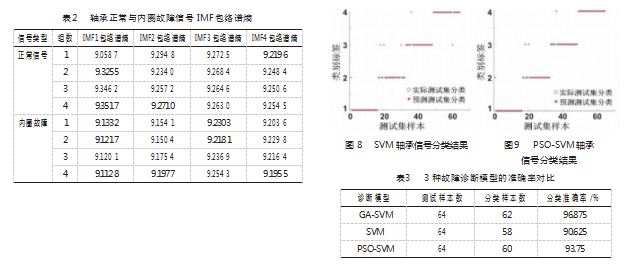
　　经过峭度准则筛选后，对前4个主要的IMF分量进行Hilbert包络谱分析，如图5所示。从图中可知，经过变换后的信号分量在不同频率处振幅会发生较大变化，具有明显谱线。由于轴承在发生故障时会掺杂不同噪声而使故障信号频谱复杂多变，将包络谱作为特征导入分类器进行识别会造成结构复杂化，而通过结合信息熵计算包络谱熵值能够有效体现包络信号变化的复杂程度，因此选取包络谱熵并归一化作为特征向量导入GA-SVM，可提高分类准确率。表2分别列举出正常信号与内圈故障信号各4组包络谱熵值。

　　3.3轴承故障信号的分类识别

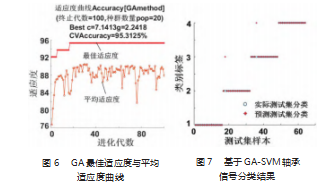
　　利用遗传算法GA优化SVM参数构造的模型，设置种群规模数量为20，最大迭代次数为200，惩罚因子C变化范围设置[0，100]，核函数参数g变化范围设置[0，1 000]，导入样本后进行全局寻优迭代，直至输出相应的适应度曲线与得到最优解。以本文分析处理并提取内圈故障信号特征的方法为例，将上述另外正常、外圈故障、滚动体故障信号各32组的样本，都进行EEMD分解、Hilbert变换、包络谱熵值计算与归一化处理形成特征向量。其中64组训练样本（4种轴承状态各16组）导入GA-SVM模型进行训练，另外64组测试样本（4种轴承状态各16组）导入训练好的GA-SVM中进行测试，类别标签y=1代表内圈故障，y=2代表滚动体故障，y=3代表外圈故障，y=4代表正常状态。如图6所示，经过100次迭代后GA-SVM模型得到最优惩罚因子Cbest=7.141 3，最优核函数参数gbest=2.241 8，分类结果如图7所示。由图可知，通过将处理好的信号特征向量导入GA-SVM进行训练与分类测试后，其对于故障的分类准确率达到96.875％。

　　为了进一步验证上述基于Hilbert包络谱熵与GA-SVM故障诊断方法的优越性，选取SVM以及粒子群算法优化后的支持向量机PSO-SVM识别模型作为对比对象，并将上述计算后相同的特征向量分别导入进行测试，结果如图8和图9所示，SVM对于故障的分类准确率为90.625％，PSO-SVM的分类准确率为93.75％。3种模型的分类结果如表3所示，通过对比可知，基于GA-SVM的轴承故障诊断模型分类准确率最高，诊断效果最好，具有一定的可行性。

　　4结束语

　　针对水轮发电机推力轴承振动信号的非稳态、非线性特征，本文提出基于Hilbert包络谱熵和GA-SVM的轴承故障诊断方法，通过轴承数据库仿真实验得出以下结论。

　　（1）采用EEMD算法对轴承振动信号进行分解，可有效改善模态混叠现象，准确提取信号特征。结合峭度准则选取出保留更多频率信息的主要IMF分量，并通过Hilbert变换与包络谱分析，计算出主要IMF分量的包络谱熵值，归一化后形成特征向量。由分析可知，不同故障类型下的IMF分量包络谱熵可以衡量信号在包络域内的频率分布情况，具有明显的表征效果。

　　（2）利用遗传算法优化SVM参数以提高分类性能，将主要IMF分量的包络谱熵作为特征向量导入其中，并对比粒子群算法等诊断模型的测试效果后可知，GA-SVM的分类准确率为96.875％，准确率最高，验证了该算法模型对于轴承故障诊断具有明显的效果与可行性。

　　参考文献：

　　[1]颜赟成,王文欢,张赛,等.水轮发电机组推力轴承故障分析及处理[J].发电设备,2022,36(2):136-140.

　　[2]李军宁,罗文广,陈武阁.面向振动信号的滚动轴承故障诊断算法综述[J].西安工业大学学报,2022,42(2):105-122.

　　[3]程军圣,于德介,杨宇.基于EMD和SVM的滚动轴承故障诊断方法[J].航空动力学报,2006(3):575-580.

　　[4]Norden E.Huang et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Se‐ries Analysis[J].Proceedings:Mathematical,Physical and Engi‐neering Sciences,1998,454(1971):903-995.

　　[5]任学平,霍灿鹏.基于EMD-AR谱和GA-BP的滚动轴承故障诊断研究[J].机电工程,2021,38(7):892-896.

　　[6]陈龙,张纯龙.基于EMD包络谱特征与PCA-PNN的滚动轴承故障诊断[J].煤矿机械,2022,43(10):173-176.

　　[7]WU Z,HUANG N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Da‐ta Analysis,2009,1(1):1-41.

　　[8]谢蓉仙,任芳,杨兆建.EEMD与HMM在齿轮故障诊断方法中的研究[J].机械设计与制造,2021(1):28-31.

　　[9]吴呈阳.基于自适应EEMD的滚动轴承故障诊断研究[D].徐州:中国矿业大学,2022.

　　[10]王玉静,那晓栋,康守强,等.基于EEMD-Hilbert包络谱和DBN的变负载下滚动轴承状态识别方法[J].中国电机工程学报,2017,37(23):6943-6950,7085.

　　[11]田博文.基于信息熵的中介轴承故障诊断[D].沈阳:沈阳航空航天大学,2021.

　　[12]Widodo A,Yang B S.Support vector machine in machine condi‐tion monitoring and fault diagnosis-ScienceDirect[J].Mechani‐cal Systems and Signal Processing,2007,21(6):2560-2574.

　　[13]孔祥媖.支持向量机和决策树算法在滚动轴承故障诊断中的应用[J].技术与市场,2023,30(2):65-68.

　　[14]刘开石,李田泽,刘东,等.基于ABC-SVM算法的光伏阵列故障诊断[J].电源技术,2021,45(9):1171-1174.

　　[15]陈园艺,孙建平.基于EEMD和PSO-SVM的滚动轴承故障诊断[J].电力科学与工程,2016,32(10):47-52.

　　[16]吕楠,姚平喜.基于BP神经网络的滚动轴承故障诊断[J].煤矿机械,2020,41(8):172-173.

　　[17]沈陆垚,师帅康.基于遗传算法优化的支持向量机的齿轮箱轴承故障识别[J].电子设计工程,2018,26(13):52-56.

　　[18]张超,陈建军,郭迅.基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J].中南大学学报(自然科学版),2012,43(3):932-939.

　　[19]郭庆丰,王成栋,刘佩森.时域指标和峭度分析法在滚动轴承故障诊断中的应用[J].机械传动,2016,40(11):172-175.

　　[20]刘臻,彭珍瑞.信息熵和合成峭度优化的VMD和PSO-SVM的轴承故障诊断[J].机械科学与技术,2021,40(10):1484-1490.