摘要：管道泄漏次声波信号中的干扰噪声影响管道泄漏定位的精准度。提出了一种基于白鲸优化算法（BWO）优化变分模态分解（VMD）联合小波阈值（WT）的管道泄漏次声波去噪方法。针对VMD算法中分解层数K和惩罚因子α的取值对信号分解结果影响较大，利用白鲸优化算法（BWO）对VMD分解的两关键参数进行寻优，获得最优参数组合[K、α]，并利用优化后的参数对次声波信号进行VMD分解，获得一系列本征模函数（IMF）分量。通过计算各IMF分量的相关系数来区分噪声IMF分量和有效IMF分量，引入一种改进的小波阈值函数对有效的IMF分量进行去噪处理，再重构去噪后各有效IMF分量，得到去噪后的管道泄漏次声波信号。通过仿真实验，将所提方法与灰狼优化算法（GWO）优化VMD联合小波阈值和麻雀搜索算法（SSA）优化VMD联合小波阈值两种方法对比，所提方法去噪后信号的信噪比分别提高了1.27%、2.01%，表明所提方法的去噪效果具有一定的优越性，为后续管道泄漏计算定位奠定了良好的基础。

　　关键词：管道泄漏次声波，信号去噪，变分模态分解，白鲸优化算法，小波阈值

　　0引言

　　管道运输由于运量大、耗能少、连续性强等优点而被广泛应用于长距离引、调水工程。但管道老化和人为破坏等原因引发的管道泄漏事故可能会造成严重的经济损失和重大的社会影响[1]。因此，当长距离管道发生泄漏后，快速准确的定位出泄漏点的位置、减少经济损失和资源的浪费尤为重要[2]。现有的管道泄漏检测方法大致可以分为3种类型：人工巡检法、硬件检测法和软件检测法[3]。近年来，基于次声波信号的管道泄漏定位方法由于其定位距离远、定位精度高、维护费用低等优点逐渐被用于长距离管道泄漏的检测定位[4]。然而，采集到的管道泄漏次声波信号中不可避免包含着干扰噪声，影响着管道泄漏定位的准确度[5]。因此，为了准确定位出管道泄漏处的位置，需要对传感器采集的信号进行去噪处理。

　　管道泄漏次声波信号是非线性非平稳信号，针对这类信号的去噪，国内外学者做了大量的研究。Drag‐omiretskiy等[6]提出了变分模态分解（Variational Mode De‐composition，VMD）算法，这是一种自适应、完全非递归的信号处理算法，通常被用于处理非线性非平稳信号。但VMD算法需要人为预设模态分解层数K和惩罚因子α,当预设值选取过大或者过小时，可能会发生信号欠分解和过分解等问题[7]。因此，如何获得VMD算法的最优参数组合[K、α]非常重要。针对这个问题，唐贵基等[8]采用中心频率观察法对K进行选取，但α确还是人为设定。冉茂霞等[9]采用粒子群算法优化VMD参数，并运用到磁瓦声振信号分析中，但粒子群算法易陷入局部最优。鲁铁定等[10]利用灰狼优化算法（Grey Wolf Optimization，GWO）获得VMD的最优K和α参数组合的GWO-VMD降噪方法，来对GNSS坐标时间序列进行降噪。魏安凯等[11]采用麻雀搜索算法（Sparrow Search Algorithm，SSA）优化VMD来实现滚动轴承振动信号的去噪。刘忠等[12]采用哈里斯鹰优化算法（Harris Hawks Optimization，HHO）对VMD参数进行寻优，并应用于水轮机空化声发射（Acoustic Emission，AE）信号的降噪中。但针对管道泄漏次声波信号的去噪方法研究较少。

　　白鲸优化算法（Beluga Whale Optimization，BWO）是2022年由大连理工大学李刚教授团队提出的一种新的基于种群的元启发式算法[13]，该算法的灵感来源于白鲸游泳、捕食和鲸鱼坠落等行为，与其他优化算法相比，该算法具有全局搜索能力和高效收敛性等优点。基于上述分析，针对管道泄漏次声波信号的去噪，本文拟采用白鲸优化算法（BWO）以最小包络熵为适应度函数，来对VMD最佳参数组合[K、α]进行寻优，引入相关系数对有效本征模函数（Intrinsic Mode Function，IMF）分量进行筛选，再联合文献[14]提出的一种改进小波阈值函数来对有效分量进行去噪后再重构，得到去噪后信号，并通过仿真对比实验来验证本文方法的有效性和优越性，为下一步对管道泄漏点的精确定位计算奠定了良好的基础。

　　1变分模态分解

　　变分模态分解（VMD）的目的是将输入信号分解为K个具有固定带宽和中心频率的IMF[15]。输入信号的分解过程实质上就是变分问题的求解过程。

　　1.1构造变分模型

　　式中：δ（t）为脉冲函数。

　　1.2求解变分模型

　　VMD算法引入了拉格朗日乘法算子λ和二次惩罚因子α来获取约束变分模型的最优解，使得约束变分问题转化为非约束变分问题[16]。得到扩展的拉格朗日函数表达式：

　　利用交替方向乘子算法（ADMM）迭代不断更新各个模态分量及其中心频率，最后得到无约束模型的鞍点，即初始问题的最佳解，所有的模态分量都可以根据频域空间由式（3）可得：

　　式中：+1(ω)，(ω)，(ω)分别为uk(t)，f(t)，λ(t)的傅里叶变换。

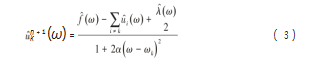
　　该算法基于各分量功率谱的重心，重新估计了重心频率，具体过程如下：

　　2白鲸优化算法

　　白鲸优化算法（BWO）主要包括勘探、开发以及鲸坠3个计算过程。且该算法中的鲸落概率和平衡因子是自适应的，对控制探索和开发能力起着重要作用。

　　由于BWO算法是基于种群的机制，白鲸在此被视为搜索代理，每一头白鲸在优化过程中都充当着候选解，并不断更新[17]。搜索代理的位置矩阵建模如下：

　　式中：t为当前迭代次数；T为总迭代次数；B0为（0，1）范围中的随机值，在每次迭代中都会发生改变。平衡因子Bf>0.5时为探索阶段，Bf≤0.5时为开发阶段。

　　2.1探索阶段

　　BWO算法的探索阶段灵感来源于白鲸的游动行为，搜索代理的位置由白鲸的配对游动决定，白鲸的位置更新如下：

　　式中：x,为下一个迭代时第i个个体在第j维上的位置；p为随机整数，假设问题维度为D，则p表示[1，D]范围内的一个随机整数，因此，x,j表示为当前迭代下第i个个体在随机维度p上的位置；r也是随机整数，假设种群规模为N，则r为范围[1，N]内的一个随机整数，因此，x,p表示当前迭代下，随机个体r在随机维度p上的位置；r1和r2均为（0，1）之间的随机数。

　　2.2开发阶段

　　BWO算法的开发阶段灵感来源于白鲸的捕食行为。为了增强该算法的收敛性，在开发阶段引入了Levy飞行策略，假设白鲸采用此飞行策略捕捉食物，其数学模型表示为：

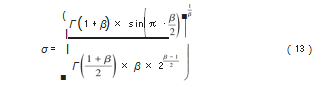
　　式中：μ,ν均为服从正态分布的随机数；β为常数，值为1.5。

　　2.3鲸鱼坠落阶段

　　为了保证种群规模大小不变，使用白鲸当前位置和鲸鱼下坠的步长来建立位置更新公式：

　　式中：r5、r6和r7为（0，1）之间的随机数，xstep为鲸鱼坠落的步长C2=2Wf×n，为与鲸鱼下降概率和种群规模相关的阶跃因子；Ub与Lb分别为变量的上限和下限。可以看出，鲸鱼坠落的步长受问题变量边界、当前迭代次数和最大迭代次数的影响。

　　鲸鱼坠落的概率（Wf）被设计为一个线性函数：

　　3小波阈值去噪

　　小波阈值去噪方法认为小波系数包含信号的重要信息。选择恰当的小波基和分解层数对含噪信号进行分解，可获得两类小波系数。一类是包含有用信号信息的小波系数，其能量主要集中在低频区域；另一类是包含噪声信号信息的小波系数，其能量主要集中在高频区域。因此可根据这一特点来辨别有用信号和噪声信号[18]。

　　小波阈值去噪的本质是抑制信号中无用部分、增强有用部分的过程，在去噪的过程中，选择一个合适的阈值函数非常关键。目前最常见的阈值函数有硬阈值和软阈值两种，其表达式为：

　　式中：ωj，k为含噪信号小波变换后对应的小波分解系数；λ为设定的阈值；sgn（）为符号函数；Wj,k为阈值处理后的小波系数估计值。

　　然而，两种阈值函数都存在着不足之处，例如硬阈值函数在阈值点处不连续，而使用软阈值函数对信号处理后，得到的小波估计系数与含噪信号的小波系数之间会产生偏差，这些因素仍然可能会影响目标信号的去噪效果。所以本文采用文献[14]提出的一种改进的阈值函数，其表达式如下：

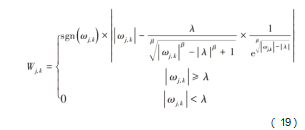
　　其中，ωj,k为含噪信号小波变换后对应的小波分解系数，Wj,k为阈值处理后的小波系数估计值。该方法添加了两个调节阈值函数的参数(α和β),通过改变两参数的数值，可以实现有效信号能量的保留，从而解决了传统软阈值函数中的恒定误差问题。

　　4 BWO-VMD联合小波阈值处理

　　在对泄漏次声波信号进行VMD分解时，需要设置好合适的分解层数K和惩罚参数α,当K的取值过大会导致出现失真现象，过小则会欠分解，造成模态混叠；同理，当α的取值过大会造成频带信息丢失，过小则会导致出现频率交叉现象，因此需要确定好最佳的组合参数[K，α]。为了达到这个目的，本文提出一种采用BWO对VMD进行组合参数寻优的方法，具体步骤如下。

　　（1）参数初始化。设定好种群数量n、最大迭代次数Tmax等初始参数。

　　（2）设置适应度函数。选择最小包络熵作为BWO优化VMD参数的适应度函数。包络熵代表原始信号的稀疏特性[19]，当IMF分量中含噪较多，特征信息较少，包络熵值则越大，反之包络熵值则越小，分量信号越简单，复杂程度越低，规律性越强。包络熵的数学表达式为：

　　式中：a(j)为IMF分量经过Hilbert解调后所得的包络信号；pj为a(j)的归一化形式。

　　利用BWO优化算法对VMD的最佳参数组合[K，α]进行寻优。

　　（3）循环迭代直到满足终止条件，输出VMD最佳参数组合[K，α]。

　　（4）将最佳参数组合代入VMD，对输入信号进行分解，获得相应的K个模态分量，然后计算每个模态分量与原始信号的相关系数，相关系数代表IMF分量与原始信号的相关程度[20]，表达式为：

　　式中：Ri表示IMF分量u(t)与原始信号x(t)的相关系数，其值越大，说明相关程度越高，对应的IMF分量中噪声含量则越低。利用相关系数的大小对IMF分量进行筛选，保留相关性较高的IMF分量，排除相关性较低或无用的分量[21]。本文设定的相关系数阈值为0.5。

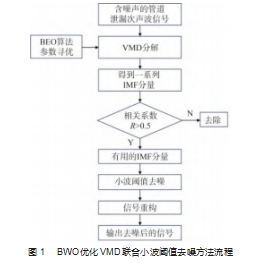
　　获得相关性较高的几个有效IMF分量之后，首先对其进行小波阈值去噪，然后再重构各分量。图1所示为BWO优化VMD联合小波阈值去噪方法的流程图。

　　5仿真实验验证

　　由于管道周围环境的复杂性，导致泄漏产生的次声波信号具有非线性、和典型的非平稳性等特点，因此构造一个非线性次声波仿真信号来验证BWO优化VMD联合小波阈值的去噪方法的可行性。构造由不同频率谐波信号组成的纯净信号x(t)，x(t)如式（22）所示。向纯净信号x(t)中加入随机高斯白噪声，得到含噪信号s(t)。设置采样点数为1 000，2种信号的时域图和频谱图分别如图2、图3所示，图中时域图横坐标为采样点数，频谱图横坐标为频率，纵坐标皆为振幅。

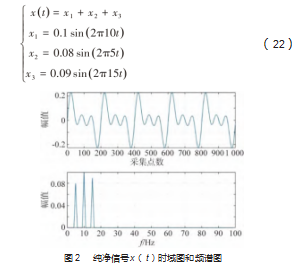
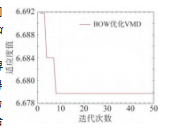
　　使用本文算法对含噪信号s(t)进行去噪处理，以最小包络熵为适应度函数通过BWO算法寻优获得VMD分解的最优参数组合[K，α]。设置种群数为20，最大迭代次数50次，分解层数K范围设为3~15，惩罚因子α范围设为1 000~15 000。BWO优化VMD迭代寻优曲线如图4所示，得到全局最优适应度值为6.677 8，最优参数组合值为K=10，α=10 289。

　　代入优化得到的最佳参数组合对包含噪声的信号s(t)进行VMD分解，得到了s(t)的10个IMF分量以及它们对应的频谱图，具体如图5所示。从图中可以观察到，IMF1分量的中心频率约在10 Hz左右，最接近原始信号的频率。

　　然后计算各分量与含噪信号s(t)的相关系数R，结果如表1所示。从表中可以得知IMF1分量的相关系数值为0.723 3，高于设定的阈值0.5，因此IMF1为主要模态分量，其他低于设定阈值的IMF分量则被视为噪声分量而舍弃掉。

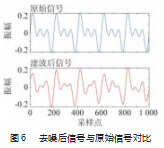
　　最后，采用文献[14]中改进的阈值函数对主要模态分量IMF1进行小波阈值去噪处理，选择db4小波基函数，进行3层分解。随后再重构分量，从而获得去噪后的信号，如图6所示。

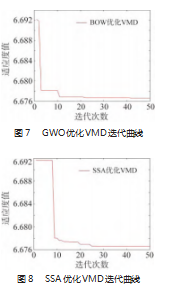
　　为了验证白鲸算法（BWO）优化VMD的优越性，与麻雀搜索算法优化变分模态分解算法（SSA-VMD）和灰狼优化算法优化变分模态分解算法（GWO-VMD）作对比，且所有优化算法在寻优过程中均采用最小包络熵作为适应度函数，分解层数K的搜索范围全部设为[3，15]，惩罚因子α的搜索范围设为[10 000，15 000]，各个优化算法的寻优迭代过程如图7~8所示。

　　引入常用的两个去噪性能指标信噪比（SNR）和均方差（MSE）来对这几种方法的去噪效果进行评定，其公式如式（23）所示。其中，SNR越大，MSE越小，则表明去噪效果越好。3种方法寻优得到的最优参数组合[K，α]以及对应的SNRMSE的结果如表2所示。

　　从3种优化算法的迭代曲线图以及表2可知，本文提出的白鲸算法优化VMD的迭代速度更快、效果更好，去噪后得到的信号信噪比最大，均方差最小，从而验证了本文方法对管道泄漏次声波信号的去噪效果有一定的有效性和优越性。

　　6结束语

　　为了提高管道泄漏定位的精准度，针对采集的管道泄漏次声波信号中存在着干扰噪声问题，提出了一种基于BWO优化VMD联合小波阈值处理的去噪方法。

　　（1）针对VMD算法对信号进行分解时易受参数K和α影响的问题，利用BWO（白鲸优化算法）来优化VMD参数K和α的值，选取最小包络熵作为BWO优化VMD的适应度函数对K和α的最优参数组合进行寻优。

　　（2）为了辨别有效IMF分量和噪声IMF分量，本文引入了相关系数R来对VMD分解之后的IMF分量进行区分。

　　（3）针对传统小波硬阈值函数在阈值点处不连续、软阈值处理后小波系数存在偏差的问题，采用一种改进的小波阈值函数对有效IMF分量进行去噪，再对去噪后的所有IMF分量进行重构。

　　采用SNR和MSE两个指标评价去噪效果，通过与SSA-VMD-WT，GWO-VMD-WT相比，本文提出的方法具有较高的SNR和较低的MSE，验证了本文方法对含有干扰噪声的管道泄漏次声波信号的去噪效果有一定的有效性和优越性。

　　参考文献：

　　[1]程玉泉,李炜杰,程诗棋.长距离大口径PCCP输水管道智慧化预警和值守技术探讨[J].水利科技,2023,(2):33-37.

　　[2]GUO Chengchao,SHI Kunming,CHU Xuanxuan.Experimental study on leakage monitoring of pressurized water pipeline based on fiber optic hydrophone[J].Water Supply,2019,19:2347-2358.

　　[3]袁文强,郎宪明,曹江涛,等.基于声波法的管道泄漏检测技术研究进展[J].油气储运,2023,42(2):141-151.

　　[4]郭颖,杨理践,唐滕达.Wavelet-VMD融合算法在管道泄漏检测的研究与应用[J].电子设计工程,2022,30(15):70-75.

　　[5]路敬祎,李佳丽,侯轶轩,等.基于VMD-MD的油气管道泄漏信号去噪方法[J].压力容器,2023,40(5):44-52.

　　[6]DRANGOMIRETSKIY K,ZOOSO D.Variational mode decompo‐sition[J].IEEE Transactions on Signal Processing,2014,62(3):531-544.

　　[7]张伟萍,付民,张海燕,等.改进的WOA-VMD算法在水声信号去噪中的应用[J].中国海洋大学学报(自然科学版),2023,53(1):138-146.

　　[8]唐贵基,刘尚坤.基于VMD和谱峭度的滚动轴承早期故障诊断方法[J].中国测试,2017,43(9):112-117.

　　[9]冉茂霞,黄沁元,刘鑫,等.基于优化变分模态分解的磁瓦内部缺陷检测[J].浙江大学学报(工学版),2020,54(11):2158-2168.

　　[10]鲁铁定,何锦亮,贺小星,等.参数优化变分模态分解的GNSS坐标时间序列降噪方法[J/OL].武汉大学学报(信息科学版),1-5.https://doi.org/10.13203/j.whugis20220363.

　　[11]魏安凯,王娜,丁军航,等.基于优化SSA-VMD的滚动轴承故障信号降噪方法[J/OL].电子设计工程,1-5.https://link.cnki.net/urlid/61.1477.tn.20231020.1010.002.

　　[12]刘忠,潘宜桦,邹淑云,等.基于优化VMD组合降噪和LMD的水轮机空化声发射信号特征提取[J].排灌机械工程学报,2022,40(10):1007-1013.

　　[13]ZHONG Changting,LI Gang,MENG Zeng.Beluga whale optimi‐zation:a novel nature-inspired metaheuristic alg-orithm[J].Knowledge-Based Systems,2022,251:109215.

　　[14]乔云,李琼,钱浩东,等.基于VMD与改进小波阈值的地震信号去噪方法研究[J].物探化探计算技术,2021,43(6):690-696.

　　[15]严孝强,张振京,宋业栋,等.基于优化VMD和SVM的柴油机故障诊断算法[J].机电工程技术,2022,51(10):279-283.

　　[16]刘伯相,张远民,江竹.基于变分模态分解的管道泄漏信号降噪方法[J].振动、测试与诊断,2023,43(02):397-403,416.

　　[17]赵小惠,杨文彬,胡胜,等.基于VMD能量权重法与BWO-SVM的铣刀磨损状态监测[J].机电工程,2022,39(12):1762-1768.

　　[18]张琳梅.基于小波阈值处理的MEMS矢量水听器信号去噪方法[D].太原:中北大学,2020.

　　[19]杨厚明,鲁铁定,孙喜文,等.SSA-VMD与小波分解结合的GNSS坐标时序降噪方法[J/OL].大地测量与地球动力学,1-11.https://doi.org/10.14075/j.jgg.2023.07.105

　　[20]施晶,朱明,沈华,等.基于VMD和小波阈值的水听器信号去噪方法[J].传感技术学报,2020,33(7):1003-1012.

　　[21]施晶.光纤水听系统的目标信号提取技术研究[D].南京:南京理工大学,2021.