摘要：属性群决策是现代企业决策的重要研究内容之一。针对专家之间信任关系动态变化对群体共识形成的影响，本文构建了基于动态信任关系的区间群决策模型。首先，依据专家个人判断信息最小偏差准则而非集结算子重新定义专家意见最优集结矩阵，并基于相对相似度提出专家个人权重的确定方法；其次，通过区间熵—集值统计求解属性客观权重；最后，通过专家之间的意见相似度建立专家的动态信任关系，并据此提出基于动态信任关系的专家共识意见调整方法，以修正个人共识度未达到阈值的专家意见，从而提高群体共识度。

　　关键词：群决策；模型；动态信任关系

　　一、引言　
      多属性群决策是现代企业决策的重要研究内容之一，具有广泛的应用背景[1-6]。本文首先基于依据专家个人判断信息最小偏差准则而非集结算子重新定义了专家意见最优集结矩阵，基于相对相似度提出专家个人权重的确定方法；其次，通过区间熵—集值统计求解属性客观权重；最后，通过专家之间的意见相似度建立专家的动态信任关系，并以此提出一种基于动态信任关系的专家共识意见调整方法，以修正个人共识度未达到阈值的专家意见，以提高群体共识度。

　　二、理论知识

　　定义1[7]记=[xL,xU]={xxL≤x≤xU,xL、xU∈R}，称为一个区间数。其中，xU为上极限，称为区间数的大元；[xL为下极限，称为区间数的小元。特别的，0≤[xL≤xU≤1，则称为一个标准型区间数；若[xL=xU，则退化为一个实数；c=xU−xL表示区间数的宽度，当c=0时，也是一个实数。

　　定义2[8]设任意两个规范区间=[xL,xU]，=[yL,yU]，称

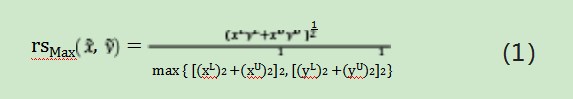
　　为规范区间数与的Max型相对相似度。已知，rsMax(,)越小，则与相似程度越小。特别的，当rsMax(,)=1时，就有，即规范区间数与完全相似。

　　三、模型构建

　　(一)问题描述

　　假设A=a1,a2,…,am为备选方案集合，D=d1，d2，…，dt为专家集合，U=u1，u2，…，un为属性集合，ω={ω1,ω2...ωj}表示属性权重向量；λ={λ1,λ2...λk}表示专家权重向量。专家dk所对应的决策矩阵为：Yk=([yL，yU])m×n，其中为是专家dk对备选方案am属性uj的评价值。

　　(二)专家权重λk的确定方法

　　在决策过程中，大部分专家往往根据个人偏好选择对方案进行评价，导致群体决策结果往往不一致。针对该问题，本文利用专家个人判断信息偏离最小得出专家意见最优集结矩阵并作为专家意见可信度衡量标准，当专家个人判断信息与专家意见最优集结矩阵越接近，专家个人的决策意见越可信，应该赋予更高的权重。

　　首先，根据集值统计公式计算出规范化区间型决策矩阵Rk=()m×n的区间数中点值。

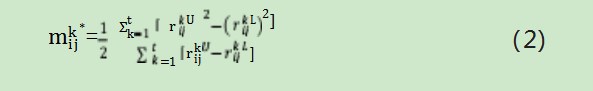
　　其次，根据区间半径与其他评估区间半径偏离最小准则，专家意见最优集结矩阵∗+=mc∗+的半径c∗+可由如下优化模型求得：

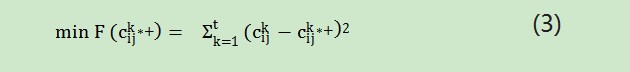
　　由此可得，专家群体关于方案ai属性uj的群体意见最优集结矩阵。

　　最后，利用相对相似度描述专家个体与专家意见最优集结矩阵的贴近度，该方法能很好地避免强调专家意见一致性而忽略部分专家的不同意见问题的出现，通过将专家意见测度数据序列的曲线形状、几何位置关系的接近水平与相似程度融合在一起，表征专家之间的联系和差异。

　　如前文所述，本文将基于最优专家意见最优集结矩阵的型相对相似度获得专家个人的意见与群体意见的相似度。

　　专家个人与最优专家意见最优集结矩Max的型相对相似度：

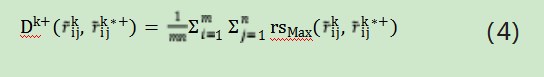
　　对其进行归一化处理，得到专家dk所对应的专权重λk：

　　(三)基于区间熵—集值统计的确定属性客观权重

　　针对专家评价值为区间数情形，本文先采用区间熵来衡量群决策中某个属性评价结果的一致性，并采用集值统计方法集结专家对属性客观权重的意见，继而给出该属性的客观权重。不同专家对同一方案的同一属性所给出的评价值越一致，则该属性的熵值越大，属性权重越小。

　　首先，计算指标uj的熵值。

　　考虑到r∈[rL,rU]，根据信息熵得，指标uj得熵值为

　　假定当r=0时，r ln r=0.

　　其次，为了确定区间熵值，值H=[HL，HU]可建立如下优化模型:

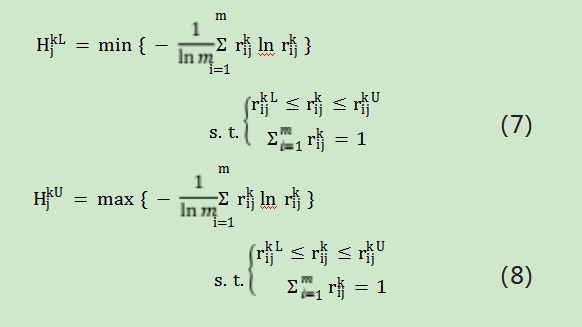
　　再次，根据由式(7)、(8)求得指标的区间熵熵HL,HU，j=1,2,…,n，得指标uj的区间熵权w=[wL，wU]可由下式计算

　　最后，根据加权集值统计公式计算出指标的特征值，设专家对第项指标的特征值为φj，则

　　由式(10)求出uj特征值φj后再将其归一化，即得出指标uj的客观权重

　　(四)基于动态信任关系的专家共识意见调整方法

　　在群决策过程中，由于专家之间个人偏好、专业背景、知识结构及经验水平等的不同，专家决策意见不可避免地存在较大分歧甚至出现意见冲突的情况。因此，为了提高决策质量，群体意见共识性分析需要重点讨论。

　　为此，本文提出了一种基于动态信任关系的专家共识意见调整方法。该调整方法由信任关系确定专家共识意见的调整系数，平衡了专家自身意见坚持程度和调整自身意见的程度，能最大程度地降低被强制要求调整意见的个别专家的工作不满意度。同时，不减少专家意见调整轮数，而提升群体共识意见达成过程的效率。

　　1.专家对每个方案进行评估，得到所对应的决策矩阵，并由管理人员和专家讨论给出全局共识性阈值φ。

　　2.对专家意见之间的共识水平进行测定。

　　关于对专家意见共识性的测度主要从计算专家个体之间评估意见的距离以定义共识性测度。

　　定义3(群体共识度)专家群体意见共识水平测度为：

　　其中，D(,ro)为和ro的欧氏距离。

　　3.将专家群体意见共识水平测度与阈值φ进行比较。若GCL≥φ,，说明群体共识性水平能被管理人员接受，则直接调转至step6；若GCL<φ，则说明存在与群体专家意见共识分歧大的个体专家意见，需分别将专家个体意见共识水平测度CL与阈值φ比较，调整专家个体意见共识水平测度小φ的专家意见，具体调整方法转向下一步。

　　4.在得到每位专家的评估值后，根据公式(1)得到专家意见之间的相似度

　　继而建立信任矩阵conft×t，并以此作为专家意见调整系数。

　　其中，simids−k为专家ds与专家dk的意见相似度。明显的，信任矩阵conft×t为一致性矩阵。

　　在给出信任矩阵conft×t后，根据公式(13)得出信任关系所对应的调整系数。ηsk表示专家ds对于自身上一轮意见的调整系数，其个人意见越倾向于向其所信任专家dk的意见方向调整。

　　随着意见调整轮数的增加，关于专家ds对其所信任专家dk的信任程度被更新，第q+1轮的信任程度来自第q轮信任程度和第第q-1轮的信任程度，通过继承历史部分信任度，增添当前部分信任度的信任关系更新策略，用动态更新因子以控制和调整更新速度，有

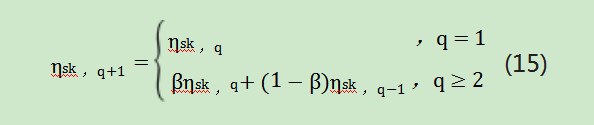
　　本文假设β=0.5时，专家认为历史信任数据和当前信任数据同样重要。

　　针对未有达到阈值的专家，其调整后的专家意见由公式(16)得出，。q表示专家ds的第q轮调整的专家个人意见。并再次判断其是否达到阈值。如果调整后的共识水平仍低于阈值，则继续对评估值进行新一轮调整。

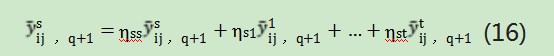
　　5.再次将专家群体意见共识水平测度与阈值进行比较。若GCLφ，则进入下一步；否则转向2。

　　6.在得到能被管理人员接受专家个体意见后，采用IWAA算子(区间数加权算术平均算子)集结各专家个体意见，得出专家群体综合评价值，并进行方案选择。

　　四、算例分析

　　本文以文献中所使用的数据为例，验证模型的适用性。电池生产企业通常需要选择一个合适的逆向物流供应商进行逆向物流合作。某电池制造企业准备对该市4家逆向物流供应商进行评估，该企业邀请4位专家根据逆向物流成本、退货率、质量、技术/工程能力对4家逆向物流供应商进行综合考查。其中，逆向物流成本、退货率为成本型指标，质量、技术/工程能力为效益型指标。

　　(1)分别将专家个体决策矩阵进行规范化处理，并根据式(2)(3)可得专家意见最优集结矩阵，并对其规范化处理，得到Rk*。继而根据式(11)可得专家权重。

　　(2)根据区间熵公式计算得各专家对应于指标uj的属性客观区间权重。然后根据加权集值统计公式集结专家意见并归一化处理，计算得到属性客观权重。

　　(3)分别求专家个人决策矩阵与群体决策矩阵的共识水平，并根据式(13)测定群体共识水平。将公式水平与阈值φ=0.95进行比较并确定需要调整得专家个人意见。

　　GCL=0.936<0.95

　　(4)由公式(14)知，CLd 1=0.939,CLd2=0.939,CLd3=0.936,CLd4=0.958，专家d 1、d2、d3的个人共识水平均小于0.95。需调整专家d1、d2、d3的专家意见。

　　根据式(14)得到每位专家与其他专家的信任矩阵conft×t。

　　由公式(15)和公式(16)得专家d1、d2、d3的调整系数，并对专家d1、d2、d3的个人意见进行调整，从而得到专家d1、d2、d3新一轮的个人决策矩阵群体意见决策矩阵。

　　根据新一轮的专家个人决策矩阵及群体决策矩阵，重新计算群体的共识水平分别为GCL=0.968，与阈值φ相比可知，所有专家的共识水平均达到阈值。

　　(5)在得到达到阈值的专家个体意见之后，由式(17)得出专家群体综合评价值。

　　(6)根据定义4对综合评价值i(i=1,2,3,4)的大小进行比较并降序排列，该结果与文献[7]的结果一致，由此可验证该模型的可行性。

　　五、结语

　　本文研究了群决策的完整过程，即评估过程、共识过程和选择过程。在评估过程中，重新定义了符合绝大多数专家意见的最优集结矩阵，并在此基础上，根据专家个人意见最优集结矩阵的相对相似度确定专家个人权重。同时，通过区间熵—集值统计求得指标属性的客观权重；在共识过程中，通过专家意见相似度衡量专家之间的动态信任关系，以确定专家共识意见调整系数，继而同时调整多个未达到阈值的专家意见；在选择过程中，通过求解各方案的综合判断区间与最优方案理想区间的相对相似度，对方案进行优劣排序。为了验证该方法的可行性，本文采用相关学者的案例进行比较分析。通过算例验证表明，本文所提出的方法，一方面，能够很好地发挥专家的主观意愿，保留专家群体智慧，使结果更加合理；另一方面，能大幅度地提高个体专家的共识水平，提升群体共识意见达成的效率。

       [1]Hosseini Dehshiri S J，Emamat M S M M，Amiri M.A novelgroup BWM approach to evaluate the implementation criteria of blockchain technology in the automotive industry supply chain[J].Expert Systems with Applications，2022(2)：198.

　　[2]Tang M，Liao H，Kou G.Typeαand typeγconsensusfor multi-stage emergency group decision making based on mining consensus sequences[J].Journal of the Operational Research Society，2022，73(2)：365-381.

　　[3]罗日洪，黄锦林，张志伟，等.基于改进AHP-FCE法的渡槽安全评价[J].河海大学学报(自然科学版)，2020，49(2)：1-9.

　　[4]李倩，王普，王秀村，等.基于改进多属性群决策的高速铁路建设项目质量管理绩效评价[J].铁道学报，2018，40(5)：156-163.

　　[5]张熠.基于D-S证据理论和TFAHP-TOPSIS的工程项目评标决策模型[J].统计与决策，2018，34(11)：48-51.

　　[6]Wu J，Zhao Z，Sun Q，et al.A maximum self-esteemdegree based feedback mechanism for group consensus reaching with the distributed linguistic trust propagation in social network[J].Information Fusion，2021(67)：80-93.

　　[7]徐泽水.不确定多属性决策方法及其应用[M].清华大学出版社，2004.

　　[8]黄智力，罗键.属性值为区间数的决策对象相对相似规划模型[J].系统工程理论与实践，2019，39(3)：766-775.