摘要：玉米是我国主要农作物之一，是重要的粮食作物和饲料作物。随着国家农业现代化的逐步发展，玉米在农业生产中的地位日益重要。研究国内玉米市场的波动，分析玉米市场的供给需求，能够帮助农业生产者做好生产决策，为政府制定政策提供依据、从而做好市场预测，防范市场风险。对于发展中国式农业现代化、维护国家粮食安全、贯彻乡村振兴战略具有重要意义。本文将以蛛网模型和回归模型的理论为基础，综合运用两种模型对国内玉米市场的供给和需求进行分析，判断国内玉米市场的稳定情况，预测国内玉米市场。以期为相关农贸企业提供借鉴和参考。

　　关键词：玉米市场、蛛网模型、回归模型

　　一、研究背景

　　玉米是我国最主要的农作物之一，我国玉米种植面积广、产量大。玉米在我国具有重要的地位。玉米市场牵扯到人民口粮需求、农业就业、农民收入、养殖业加工业等相关行业发展、粮食安全等多个方面。近年来，国际形势动荡不安，各类事件频发。玉米价格跌宕起伏，波动不断。2022年初，受新冠肺炎疫情影响，玉米市场流通受限。在俄乌冲突和新冠病毒疫情对国内外粮食供应链的持续扰动下，玉米价格再创新高。由此可见，在经济高速发展的今天，玉米作为我国第一大粮食品种，市场价格仍不稳定，受到多方因素的影响。因此，研究玉米市场的波动具有重要意义。党的二十大报告对粮食安全作出重要指示，要“全方位夯实粮食安全根基”，“确保中国人的饭碗牢牢端在自己手中”。研究玉米市场波动，做好玉米市场预测和风险管理，才能更好地维护粮食安全。同时，研究玉米市场波动也能为农业生产、政策制定提供决策依据，为发展中国式农业现代化，乡村振兴作出重大贡献。

　　二、理论模型

　　(一)蛛网模型

　　蛛网模型是由H.Schultz、U.Ricel和J.Tinbergen分别提出，1934年由英国经济学家N.Kaldor命名的经济学模型，用于解释市场中价格和数量的动态波动现象。蛛网模型的研究对象是市场上某种商品的数量和价格随时间的变化规律。

　　假设第k时段的商品数量为，价格为，假设同一时段商品价格取决于数量，当商品处于平衡状态时，数量为，价格为。设需求函数为：

　　根据上述的差分方程推导，蛛网模型分为两种类型：

　　1.收敛性蛛网

　　当需求曲线斜率绝对值大于供给曲线绝对值时，市场经济稳定，商品的数量和价格的震荡将趋向稳定，蛛网模型呈现为收敛型。

　　2.发散型蛛网

　　当需求曲线斜率绝对值小于供给需求斜率绝对值时，市场经济不稳定，商品数量和价格将出现越来越大的震荡，蛛网模型呈现为发散型。

　　(二)回归模型

　　1.回归分析概述

　　回归模型是一种统计分析方法，是通过一个自变量或若干个自变量的变化解释因变量的变化。回归模型可以用于确定因变量与自变量之间的关系，还可以由回归方程进行数量上的预测和控制。回归模型估计使用最小二乘法，其数学原理是通过求极值得到回归系数，拟合出一条最佳直线，使各散点与所拟合直线之间距离的平方和最小。回归模型根据自变量的个数分类，可以分为一元回归和多元回归分析；按照因变量的个数分类，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型分类，可分为线性回归分析和非线性回归分析。本文将采用的回归类型为一元线性回归。

　　2.一元线性回归模型检验

　　(1)拟合优度检验

　　通过判断系数R2来判断回归方程的拟合程度。R2表示在y的总平方和中，解释变量能被解释的百分比。判定系数的取值在0至1之间，判定系数越接近1，线性拟合程度越高，自变量对因变量的影响越大；越接近于0，线性拟合程度越低，自变量对因变量的影响越小。

　　(2)估计标准误差

　　估计标准误差是衡量因变量实际值与拟合值之间的平均离差大小的统计量。估计标准误差从残差平方和的角度评价回归模型的拟合效果。估计标准误差越小，一元线性回归模型的拟合效果越好，反之则越差。

　　(3)单参数显著性检验

　　回归模型的数学形式是通过散点图确定的，因此精度不高，需要对回归模型的参数进行检验。由于总体方差未知，故使用t检验法对回归参数进行显著性检验。且一般人们更关心自变量对因变量的影响是否显著，因此对回归系数b1的检验更为重要。

　　(4)模型整体显著性检验

　　为检验回归模型是否显著成立，需要对模型进行F检验。F检验是对模型的总体显著性进行检验。检验全部解释变量对被解释变量的共同影响是否显著。在一元线性回归中解释变量与被解释变量都只有一个，因此F检验等同于t检验。

　　本文将运用回归模型，求出国内玉米市场的需求供给函数，结合蛛网模型的理论，判断国内玉米市场波动情况，并提出相关政策建议。

　　三、数据分析处理

　　(一)数据来源

　　本研究数据来源于《中国农产品价格调查年鉴》《中国统计年鉴》和《2023-2029年中国玉米种子行业市场深度分析及发展规模预测报告》。研究数据可信度高，符合统计数据的准确性、及时性、完整性要求。

　　表1 2003-2020年国内玉米市场产量、需求量及价格

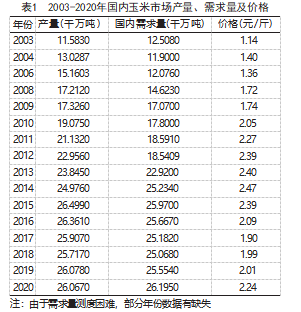
　　(二)数据分析

　　基于表1中的数据，以上一期玉米价格作为自变量，本期玉米产量为因变量，借助MATLAB软件对2004~2020年的玉米产量和2003~2019年玉米价格数据进行回归分析。得到国内玉米市场供给函数为：y=3.4623+9.5429x。回归模型判定系数为0.74，模型中度拟合。F检验P值远小于0.01，模型总体显著性高。t检验P值远小于0.01，回归系数显著。

　　以本期玉米价格为自变量，本期玉米需求量为因变量，使用MATLAB软件对2003~2020年玉米需求量和2003~2020年玉米价格数据进行回归分析。得到国内玉米市场需求函数为：y=0.2933+10.146x。回归模型判定系数为0.561，模型中度拟合。F检验P值0.00084小于0.01，模型总体显著性高。t检验P值远小于0.01，回归系数显著。

　　(三)回归模型评价

　　根据MATLAB软件回归结果，国内玉米市场供给函数和需求函数的判定系数不高，还有待改进。但模型经过了F检验和t检验，模型总体显著性高，回归系数显著。模型总体可用。由于玉米的需求弹性小，因此回归模型预测的准确度不高，但仍然可以通过回归模型观察国内玉米市场波动情况，为提出政策建议提供统计学依据。

　　四、研究结论

　　通过对国内玉米的产量、需求量和价格进行回归分析，得到了国内玉米市场的供给曲线和需求曲线。根据回归分析结果，国内玉米市场需求曲线的斜率为10.146，而供给曲线的斜率为9.5423。根据蛛网模型的理论介绍，可以判断国内玉米市场的蛛网模型为收敛型蛛网，这意味着从长期来看，玉米市场的经济相对稳定，玉米数量与价格的波动最终会趋向稳定状态。然而，需要注意的是，需求曲线与供给曲线的斜率接近，而回归模型的拟合效果一般。这意味着国内玉米市场的蛛网模型可能会出现发散型蛛网的情况，市场可能趋向不稳定。在这种情况下，玉米市场可能会发生不断的价格和数量波动，难以达到稳定状态。因此，综合以上分析，国内玉米市场从长期来看较为稳定，但由于需求曲线和供给曲线斜率接近且回归模型的拟合效果一般，市场可能面临发散型蛛网的风险，从而导致不稳定的情况发生。因此，在监测和管理玉米市场时，需要密切关注需求和供给的变化，并采取相应的措施来维护市场的稳定性。

　　参考文献

　　[1]姜德重.疫情反复流通受限玉米市场跌宕起伏[N].粮油市场报，2022-03-17(B03).

　　[2]王向博.2022年玉米市场回顾及2023年展望[N].粮油市场报，2023-02-14(B03).

　　[3]高举中国特色社会主义伟大旗帜为全面建设社会主义现代化国家而团结奋斗[N].人民日报，2022-10-17(02).

　　[4]Nicholas Kaldor.A Classificatory Note on the Determinatenessof Equilibrium[J].The Review of Economic Studies，1934，1(2)：122-136.

　　[5]高鸿业.西方经济学[M].北京：中国人民大学出版社，2000.

　　[6]汪洋.基于蛛网模型的中国玉米供求市场分析[J].新经济，2015，442(20)：12-14.

　　[7]刘靖文.世界主要玉米生产国生产与出口潜力研究[D].中国农业科学院，2021.

　　[8]许世卫.农业信息分析学[M].北京：高等教育出版社，2013.

　　[9]周向阳，张建华，吴建寨.构建中国玉米市场监测预警体系的思考[J].农业展望，2014，10(08)：55-58.