【摘要】文中以我国地铁突发事件应急演练为背景，在构建大客流综合处置演练评价指标体系的基础上，采用模糊评价和ＴＯＰＳＩＳ组合赋权的方法，构建城轨交通突发事件应急演练评价模型。文中以上海地铁１６号线野生动物园站大客流综合处置演练为例，综合考虑指挥统筹、关键流程控制、岗位协作以及信息传递四个方面的评估因素，运用模糊评价方法，建立了各个指标的权重，并利用ＴＯＰＳＩＳ方法，对演练过程中各个小队的演习效果进行了评价。最后，通过算例分析，证明了模型的适用性和合理性，对于各种突发事件的评价都有一定的实用价值。

　　【关键词】城市轨道交通;演练评估;模糊评价法;ＴＯＰＳＩＳ

　　１引言

　　城市轨道交通的发展带来了新的问题，其中超大客流量及其不均衡性对运营安全构成重大挑战。举例而言，高峰期客流在时间和空间上的不均衡现象增加了运行计划、车站客运组织、应急调度指挥以及乘客出行服务等方面的安全需求。一旦出现问题，就可能导致列车延误，进而带来大客流风险。演练评估作为检验预案、完善应急准备、培训队伍、调整机制的重要手段，在应对各种突发情况和自然灾害、确保城市轨道交通安全运行方面起到至关重要的作用。通过模拟各种突发事件、故障和事故场景，演练评价不但可以评价操作管理者与设施设备之间的整体协调程度，而且可以检验有关法规和计划的可行性。然而，现实中的应急演练存在一系列问题，如科目无法全面覆盖、无法真实模拟突发现场情况、演练评估存在主观性以及内部人员评估的局限性等，这些问题均影响了应急演练的效果和作用的发挥。为了解决这些挑战，提高城市轨道交通应急演练的质量和效果，我们需要构建一套高效的应急演练评估机制。

　　当前，我国的城市轨道交通演练相关的评估理论体系正在进步和优化，所提出的评估手段也呈现出各式各样的特点。周淮[１]认为对安全运营条件和能力进行科学评估的有效方式是第三方评估模式，它同时也是确保运营安全的关键工具ꎻ李璐等[２]从建立评价系统的原理入手，结合各个车站所具有的特征，选择出对应的评价指标，通过对各个地区的指标进行分析和分级，构建一个模拟运行的安全性评价模型ꎻ阔康[３]使用层次分析法对地铁车站中的电话闭塞法演练进行安全评估ꎻ王华声等[４]运用层次分析法，从突发事件的实施效果出发，对突发事件的应急演练实施效果进行了评价ꎻ于庭安[５]采用层次分析方法，确定了城市轨道交通突发事件应急能力评估系统各指标的权重，并进行了实例分析ꎻ张丽等[６]将层次分析法与模糊综合评判法相结合，对企业的事故树进行了分析，并得出了相应的结论。姜少涌等[７]将决策实验室法(ＤＥＭＡＴＥＬ)与熵加权(Ｅｎｔｒｏｐｙ)两种方法有机地结合起来，利用博弈理论，对待评估方案进行综合加权，并采用模糊综合评判的方法，来确定待评估方案的最后得分及评分。在风险网络方面，刘丹阳，潘寒川[８]构建了一个基于ＡＨＰ－风险网络的评价模型，利用风险网络分析法得出的客观权重，对ＡＨＰ方法中获得的主观权重进行校正，使得评价指标的权重具有专业和客观两方面的特点。

　　因此，相较于层次分析法等主观确定权重的方法，本文将模糊评价和ＴＯＰＳＩＳ法相结合，构建城市轨道交通应急演练评价模型，通过模糊评价法获取各个指标的权重，并利用ＴＯＰＳＩＳ法对各个指标进行加权，从而提升应急演练评价结果的可信性。

　　２基于模糊评价－ＴＯＰＳＩＳ的应急演练评估模型

　　首先，采用模糊评价方法，将多目标决策问题分解成多层的标准与指标，通过对定性指标的模糊量化，得到各个指标的权值。然后，采用ＴＯＰＳＩＳ算法对模糊评价法所得到的权值进行排序，使其能够最大程度客观地体现出专家的主观意图。最后，将模糊评价法与ＴＯＰＳＩＳ方法相结合，构建城市轨道交

　　通应急演练评估的模糊评价－ＴＯＰＳＩＳ综合评价模型。

　　２.１构造判断矩阵

　　本研究使用１－９尺度方法来构建评判矩阵，各指标的相对重要度比较准则见表１[９]。

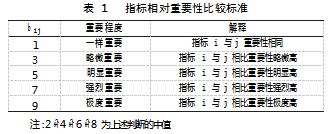
　　其中，ｂｉｊ代表指标ｉ与ｊ的比值，ｍ代表指标数量，通过各级判断因子之间的两两比较，可以得到一个判断矩阵。
       

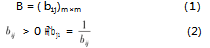
　　２.２判断矩阵一致性检验

　　设判断矩阵Ｂ的最大特征值为λｍａｘ。根据各平均一致性指标得到矩阵Ｂ的一致性指标ＩＣ，ＩＣ的计算公式为
       

　　若λｍａｘ＝ｍ，则ＩＣ＝０，则判断矩阵具有一致性，ＩＣ越大，不一致性程度越大。ＩＲ为与之对应的随机一致性平均程度指标，其取值参考表２。

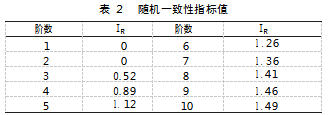
　　进一步计算一致性比率ＲＣ，其计算公式为
      

　　当ＲＣ<０.１，说明一致性检验通过，当ＲＣ>０.１，则表明一致性检验未通过，需要适当调整判断矩阵中元素的值，然后重新进行检验。

　　２.３指标权重的计算

　　指标权重的计算采用几何平均法，按照公式(５)至公式

　　(７)的步骤进行，首先，计算每一行元素相乘得到新向量ｎｉ，然后计算ｎｉ的ｍ次方根φｉ，最后对计算出的向量进行归一化，得到对应的权重值φｉ。经过计算，可以得到准则层的相对权重φ＝(φ１，φ２，…，φｋ)，随后以相同方法对下级指标层的相对权重进行计算。
       

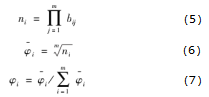
　　２.４采用ＴＯＰＳＩＳ方法计算贴近度
      ２.４.１建立加权标准化决策矩阵

　　假设有ｘ个方案组成方案集Ｆ＝{ｆ１，ｆ２，…ｆｘ}，其中，每一个方案的判断指标ξ１，ξ２，…ξｙ组成指标集ξ＝{ξ１，ξ２，…ξｙ}，对应的判断指标记为ξｉｊ(ｉ＝１，２，…，ｘꎻｊ＝１，２，…，ｙ)，其中ξｉｊ表示第ｉ个方案中第ｊ个评判指标，基于此，建立初始评判矩阵Ｆ。
       

　　对于矩阵Ｆ，通过与利用层次分析法获得的各指标权重φ相乘，即可获得加权标准化决策矩阵。
        

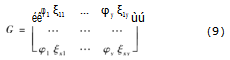
　　２.４.２确定正负理想解及相对距离

　　ＴＯＰＳＩＳ法是一种按期望目标的相似度排序进行优选的算法，其中正负理想解可以表达为
      

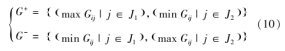
　　其中，Ｊ１和Ｊ２分别为效益型指标集和成本型指标集，Ｇ＋和Ｇ－分别为正、负理想解。

　　评价对象和正、负理想解的相对距离可表示为
      

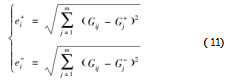
　　式中，ｅｉ＋，ｅｉ－分别为评判对象到正、负理想解的距离ꎻＧｊ＋，Ｇｊ－分别为Ｇ＋和Ｇ－中对应的元素。

　　２.４.３计算综合评价向量

　　评价对象和正理想解的贴合度可表示为
      

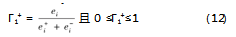
　　式中，Γｉ＋为评价对象和正理想解的贴近度，其值越大，说明越贴近正理想解。通过对评价对象的贴近度值进行排序，可以获得对方案的评价。

　　综合评价向量Ｓ可以表示为
     

　　式中，Ｓ为评价矩阵，由贴近度值组成ꎻφ代表权重，由层次分析法计算所得。

　　３实例分析

　　２０２３年８月３０日１０∶００，上海轨道交通１６号线野生动物园站至惠南站上行因为异物侵限而运行中断，导致站台大量乘客滞留，为缓解故障期间客流积压，上海申通地铁集团组织了野生动物园站大客流现场处置及公交配套保障现场处置综合演练，因而选用此站作为演练车站。

　　３.１构建城市轨道交通演练评估指标体系

　　如图１所示，本文将野生动物园站大客流应急演练评价作为目标层Ｓ，准则层Ｐ包括统筹指挥Ｐ１、关键流程控制Ｐ２、岗位协作Ｐ３、信息传递Ｐ４ꎻ指标层Ｍ包括调度做好向全线的协调发令工作Ｍ１、车站各岗位人积极响应现场指挥Ｍ２等２０项指标。

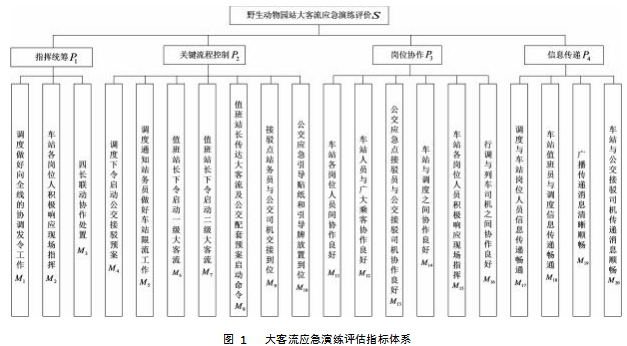
　　３.２确定权重

　　根据３.１中的指标体系，邀请城市轨道交通应急处置领域的多名专家对指标进行打分，根据评定的结果可建立准则层对应的判断矩阵Ｂ为
       

　　通过计算可得:λｍａｘ＝４，ＲＣ＝０<０.１，通过检验。根据公式(５)至公式(７)可得到准则层的权重φｉ为
      
           

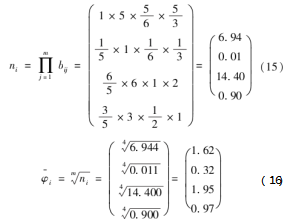
　　所以准则层指标的权重值为:φ１＝０.３３，φ２＝０.０７，φ３＝０.４０，φ４＝０.２０。这说明准则层Ｐ重要程度排序为关键流程控制>岗位协作>指挥统筹>信息传递。

　　同理，计算可得指标层各指标的权重值，权重排序如表３所示。

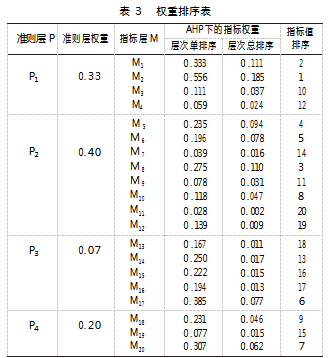
　　此次演练共有４个班组，分别为班组１、班组２、班组３、班组４，在进行打分时，评估人员根据演练现场情况，对于每一项失误，按照失误的严重程度分为Ａ、Ｂ、Ｃ、Ｄ、Ｅ五个评分等级。操作无失误为等级Ａ，记１０分ꎻ轻微失误为等级Ｂ，记７.５分ꎻ失误为等级Ｃ，记５分ꎻ重大失误为等级Ｄ，记２.５分ꎻ特别重大失误为等级Ｅ，记０分，具体评分方式如表４所示。

　　在演练结束后，评估人员通过汇总得到各个班组在每一项的得分，如表５所示。

　　３.３计算正负理想解及贴近度

　　本文以指挥统筹Ｐ１指标为例，根据公式(９)可得加权标准化决策矩阵为

　　根据公式(１０)，可直接得到正、负理想解为
       

　　根据公式(１１)，计算其正、负理想解的相对距离如表６所示。

　　根据公式(１２)，可计算各班组的贴近度为
      

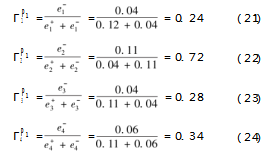
　　同理可计算出Ｐ２，Ｐ３，Ｐ４与对应正理想解的贴近度，如表７所示。

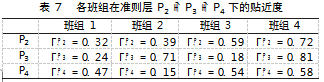
　　所以，贴近度构造的评价矩阵为
     

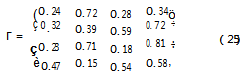
　　最后根据公式(１３)可得

　　Ｓ＝φ×Γ＝(０.３２，０.４５，０.４７，０.５７)(２６)

　　３.４结果分析

　　从演练执行效果的重要性角度来看，通过比较权重φ１，φ２，φ３，φ４的值，可以得出其重要程度排序为:关键流程控制>岗位协作>指挥统筹>信息传递。根据贴近度的评价矩阵，各班组在此次演练中的表现从优到劣排序如下:在指挥统筹方面，班组２>班组３>班组４>班组１，说明班组２在指挥统筹方面表现最佳，而班组１表现最差ꎻ在关键流程控制方面，班组４>班组３>班组２>班组１，说明班组４在关键流程控制方面表现最佳，而班组１表现最差ꎻ在岗位协作方面，班组４>班组２>班组１>班组３，说明班组４在岗位协作方面表现最佳，而班组３表现最差ꎻ在信息传递方面，班组４>班组３>班组１>班组２，说明班组４在信息传递方面表现最佳，而班组２表现最差。综合考虑总体得分，各班组得分分别为:０.３２，０.４５，０.４７，０.５７，排序为:班组４>班组３>班组２>班组１，说明整体上班组４在此次演练中表现最为出色，而班组１整体上表现最差。

　　４结语

　　针对城市轨道交通应急演练评估，本文提出了基于模糊评价－ＴＯＰＳＩＳ组合赋权的评估模型。相较于传统的层次分析法等权重计算方法，本文所提出的ＴＯＰＳＩＳ法考虑了评价指标间的相互影响与逻辑关系，减少了主观因素的干扰。同时，采用优劣解距离法计算客观权重，提升了评估结果的可信度。通过对同一演练中四个班组的表现情况进行综合排序，以及对准则层与正理想解的贴近度进行排序，直观展示了各评估对象在不同方面的优势和不足，避免了权重分配困难的问题，实现了从定性指标到定量指标的转化。最后，通过算例验证了模型的可行性和推广价值，可应用于城市轨道交通应急演练评估等相关领域。

　　[参考文献]

　　[１]周淮.城市轨道交通运营安全的第三方评估[Ｊ].城市轨道交通研究，２０２２，２５(０７):６＋２４８.

　　[２]李璐，董守放，王爱丽.城市轨道交通车站仿真运营安全状态评估方法研究及应用[Ｊ].现代城市轨道交通，２０２３(０３):７９－８４.

　　[３]阔康.基于ＡＨＰ的城市轨道交通电话闭塞法演练安全评估[Ｊ].科技资讯，２０１７，１５(１５):６８－７０＋７２.

　　[４]王华声，徐永红，曾海军，等.城市轨道交通新线试运行演练评估应用研究[Ｊ].都市快轨交通，２０１８，３１(０２):１２９－１３４.

　　[５]于庭安.我国城市地铁突发事件应急体系建设的研究[Ｄ].长沙:中南大学，２００８.

　　[６]张丽，柏萍，汪忠雨，等.基于层次分析与模糊综合评价的事故应急预案评估[Ｊ].中国安全生产科学技术，２０１５，１１

　　[７]姜少涌，李健，刘志钢，等.基于ＤＥＭＡＴＥＬ－Ｅｎｔｒｏｐｙ法的城市轨道交通应急预案评价方法研究[Ｊ].物流工程与管理，２０２３，４５(０１):１１２－１１５.

　　[８]刘丹阳，潘寒川.基于ＡＨＰ－风险网络的城市轨道交通应急演练评估研究[Ｊ].上海工程技术大学学报，２０２２，３6(０４):４１０－４１７.

　　[９]邓雪，李家铭，曾浩健，等.层次分析法权重计算方法分析及其应用研究[Ｊ].数学的实践与认识，２０１２，４２(０７):９３－１００.