摘要：文章聚焦于企业生产决策优化问题，旨在通过优化质量控制决策，在控制产品质量的同时降低生产成本，实现企业经济效益最大化。文章采用动态规划算法分析零配件、半成品及成品的质量控制及不合格品处理决策。在零配件采购环节，运用抽样检测策略，基于统计学假设检验原理，采用顺序概率比检验方案，最小化检测次数。此外，文章还考虑次品率抽样检测误差，引入贝塔分布完善最优生产决策模型，使其更贴近真实生产决策情况，提升了模型的实用性和准确性。本研究为企业生产决策提供科学依据，有助于实现产品质量与经济效益的双重提升。

　　关键词：动态规划；顺序概率比检验；贝塔分布

　　在当今激烈的市场竞争中，制造企业面临着复杂的生产决策问题，这些问题广泛存在于汽车制造、食品加工等多个行业。企业需要通过严格的质量控制流程来确保产品质量、降低风险，并最终实现经济效益［1］。这些决策涉及多个零配件和工序，包括是否对每个零配件进行检测、是否对装配完成的半成品进行检测、如何处理不合格品等。这些决策的制定需要考虑多种因素，如次品率、成本（包括零配件和成品的单价、检测成本、装配成本、拆解费用等），以及市场售价和调换损失等。因此，优化质量控制决策对于最大化企业收益和最小化成本至关重要。

　　本文旨在运用动态规划算法和顺序概率比检验方法，为多零配件和多工序的生产过程提供最优的质量控制决策方案［2］。具体而言，本文首先在零配件和成品次品率已知的条件下，针对零配件检测、装配检测、成品检测和不合格品处理等关键决策点设计决策方案，提出实现利润最大化的生产过程决策方案；其次，设计顺序概率比检验抽样检测方案［3］，以确定供应商提供的零配件是否满足次品率要求，并降低检测成本；最后，考虑次品率的不确定性，引入贝塔分布来完善不同情况下的最优生产决策模型算法，使其更贴近真实的生产决策情况［4］。

　　一、模型的建立与求解

　　（一）动态规划模型

　　1.定义状态和决策变量

　　用一个状态向量S（d1,d2,...,d16）来表示当前的决策状态，假设决策过程为检测8个零配件，检测3个半成品，拆解3个半成品，检测成品，拆解不合格成品。每个决策di∈{0,1}，表示是否在某个决策点采取行动。

　　2.定义成本和收益

　　在本文中，m为工序数量，Pi为第i个零部件的购买单价，Ci为第i个零部件的检测成本，Di为第i个零部件的次品率，C为第i个半成品的装配成本，C第i个半成品的检测成本，C为第i个半成品的拆解费用，Dh为半成品的次品率，Df为成品的次品率，Ca为成品的装配成本，Ct为成品的检测成本，Cd为成品的拆解费用，Pm为市场售价，Cr为调换损失。

　　企业的总收益来自于合格成品的销售收入，即总生产数量乘以成品的合格率Nsold=Ntotal×(1−Df)，则收益R为Pm×Nsold。不合格成品将会导致调换损失，损失费用为Crtotal=Df×Cr，最后的总利润为总收益减去总成本。

　　3.定义状态转移方程

　　状态转移方程用于描述从一个状态过渡到另一个状态的过程。在第i个决策时，如果做出选择di=1，则需要计算相应的检测或拆解成本，以及由此带来的收益；如果做出选择di=0，则意味着跳过了这个决策，不产生相应的成本或收益。每个决策都影响当前的总成本和收益，形成决策路径［5］。

　　4.初始化边界条件

　　初始条件是没有任何检测或拆解的成本，也没有任何收益，也就是还没有开始做任何检测、装配或拆解决策时，成本和收入都为零，利润为零，S（0，...，0）=0。

　　边界条件是所有决策完成时的利润S（d1,d2,...,d16）=Profit（d1,d2,...,d16），也就是说，当做出了所有决策时，可以直接计算当前状态下的总利润。

　　5.算法流程

　　（1）从初始状态开始，需要计算每个零配件的检测决策d1,d2,...,d8，并保存每个状态的结果；

　　（2）继续计算半成品检测和拆解决策d9,d10,d11,d12,d13,d14，依赖于之前的零配件检测结果；

　　（3）基于前面的决策结果，计算成品的检测和拆解决策d15,d16；

　　（4）通过递归和缓存机制，动态规划逐步缓存每个子状态的最优解，直到找到整个决策序列的最优解。

　　（二）顺序概率比检验

　　在购买零配件阶段，在供应商承诺次品率不超过一个标称值的前提下，企业采用抽样检验方法决定是否接收这批零件。本文假设两种情况。情况一：在95%的置信度下认定零配件次品率超过标称值，则拒收这批零配件；情况二：在90%的置信度下认定零配件次品率不超过标称值，则接收这批零配件。

　　顺序概率比检验（Sequential Probability Ratio Test，SPRT）是一种统计决策过程，用于在观察数据的过程中作出是否接受或拒绝原假设的决策。SPRT的核心在于计算概率比，并将其与两个预先设定的阈值进行比较。这些阈值取决于所犯第一类错误（弃真）和第二类错误（取伪）的最大可接受概率。

　　（三）加入贝塔分布后模型的建立

　　在上节中，零配件、半成品和成品的次品率均是通过抽样检测方法得到的。这是基于有限样本的估计结果，实际的总体次品率（真实值）具有一定的不确定性，其二项分布的参数可以使用贝塔分布作为其先验分布，通过抽样或贝叶斯推断的方法，贝塔分布可以表示样本次品率的后验分布。由此，其实际次品率p服从贝塔分布，表示为p~β(α,β)。具体来说，贝塔分布是一个连续概率分布，用于描述0到1之间的比例，即适合次品率、成功率等介于0和1之间的量。因此，贝塔分布能够对样本次品率的估计进行建模，表示次品率的真实值可能在某个区间内波动［6］。

　　二、实验结果与分析

　　（一）动态规划模型结果

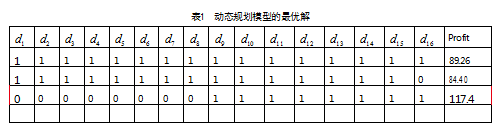
　　本文使用MATLAB，基于动态规划模型求得表1所示的最优决策为（0，0，0，0，0，0，0，0，1，1，1，1，1，1，1，1），此时的最大净收益为117.4。

　　（二）顺序概率比检验模型结果

　　假设次品率标称值为10%，对SPRT抽样过程进行1000次模拟。在情况一时，最小样本量的上四分位数为48，下四分位数为29，平均最小样本量为41；在情况二时，最小样本量的上四分位数为80，下四分位数为56，平均最小样本量为69.594。基于此，可以得出以下结论：在75%置信水平下，情况一成立时的最小样本量为48，情况二成立时的最小样本量为80。

　　（三）加入贝塔分布后模型结果

　　根据贝塔分布特点，当n值越大，也就是参与测试的样品值越高，则贝塔分布越收窄；依照贝塔分布随n值变大收窄的特点，兼顾3.2节的结果，取用n的最小可能值进行研究，进而得到更新之后的次品率值。最终，对动态规划模型进行重新求解，得到最优决策为（0，0，0，0，0，0，0，0，1，1，1，1，1，1，0，1）。

　　（四）敏感性分析

　　本文选取了零配件次品率和成品检测成本两个关键变量进行单变量的敏感性分析，观察这些变量的变化对最大利润和决策路径的影响。

　　零配件次品率是影响装配成品质量的关键因素之一，本文将其分别设定为0.05、0.07、0.1、0.12和0.15。实验结果为，最大收益分别是126、122.06、117.4、114.96和110.7。当次品率较低时，企业可以获得最高利润。随着次品率上升，企业的最佳决策路径发生了变化，需要更频繁地进行检测（次品率0.15时），利润显著下降。因此，零配件的次品率对企业利润有较大的影响，控制次品率可以提高利润。

　　成品的检测成本对企业的检测决策有重要影响。本文将其分别设定为2、4、6、8和10。实验结果为，最大收益分别是121.8、119.8、117.4、115.8和114。检测成本较低时，企业可以在不进行成品检测的情况下获得较高利润。随着检测成本的增加，企业不得不调整检测策略，检测频率的降低进一步影响了企业的利润。

　　三、结语

　　本研究通过应用动态规划算法和顺序概率比检验，优化了企业生产决策，实现了产品质量控制与成本降低的双重目标，从而最大化了经济效益。研究发现，动态规划算法能够获取最优生产决策方案，顺序概率比检验在抽样检测中能有效减少样本量，降低成本，而贝塔分布的引入则提高了模型对次品率不确定性的适应能力。敏感性分析进一步揭示了零配件次品率和成品检测成本对利润的具体影响。本研究为企业提供了科学的决策支持工具，对提高生产决策的精准度具有重要意义。

　参考文献

　　［1］潘蓉蓉，罗建强，杨子超．数字技术赋能制造企业服务化转型：理论分析与展望［J］．系统工程理论与实践，2023，43（11）：3110-3128.

　　［2］吴鹏，吕有厂．随机需求下考虑半成品库存的多周期生产决策优化［J］．运筹与管理，2014，23（2）：49-54.

　　［3］毕军贤，赵定涛．抽样检验产品的质量检验博弈与诚信机制设计［J］．管理科学学报，2011，14（5）：43-51.

　　［4］吴晓黎，杨海欣，刘雪洁．订单式生产下汽车零配件企业采购决策研究［J］．工业工程，2021，24（5）：63-71+94.

　　［5］Schnuerch M,Erdfelder E.Controlling decision errors with minimal costs:The sequential probability ratio t test［J］.Psychological Methods,2019,25(2):206-226.

　　［6］张志辉．二项分布类试验设计研究［J］．系统仿真技术，2023，19（3）：279-282.