摘要：文章通过《中国统计年鉴》选取近23年国内生产总值GDP年度数据，对GDP与九大行业间的关系进行分析，以国内生产总值GDP为被解释变量，九大行业作为解释变量，即农林牧渔业、工业、建筑业、批发和零售业、交通运输仓储和邮政业、住宿和餐饮业、金融业、房地产业、其他。基于偏相关系数选取最佳阈值0.637 5，并以此构建网络图结构，以GDP与九大行业为节点，相互之间的相依关系为边，进行网络图可视化。根据网络图可得出影响GDP的主要因素有工业、建筑业、金融业、房地产业和其他，其中除房地产业与GDP呈负相关外，其他行业与GDP呈正相关。利用网络图模型分析所得结论与多元统计方法分析所得结论相同，验证了基于偏相关系数与最佳阈值构建的网络图模型分析GDP的影响因素的正确性。但相较于多元统计方法，网络图模型使各节点间的相关关系更为清晰直观，便于理解和分析GDP的行业影响因素。

　　关键词：图模型；GDP影响因素；最佳阈值；网络图

　　前言

　　国内生产总值（Gross Domestic Product，简称GDP），是一个国家（或地区）所有常住单位在一定时期内生产活动的最终成果，是一个国家或地区经济状况和发展水平的重要衡量指标。当一个国家的GDP迅速增长，反映出该国经济蓬勃发展，国民收入增加，国内需求水平增加，人民消费水平也随之增加。可以说，GDP在一定程度上反映出一个国家的整体发展水平，包括经济层面、国民生活等。

　　国内外已有许多学者对GDP影响因素进行了实证分析，通常采用计量经济分析方法，建立的经济计量模型不同，分析结果有所不同。例如Feng等运用OLS模型，得出投资和居民消费对GDP增长有显著影响，而净出口对GDP增长的影响不显著；Kira[3]采用凯恩斯模型对坦桑尼亚1970—2009年的GDP进行检验，得出其国内生产总值受到消费（政府最终支出和家庭最终支出）和出口的影响。赵浩然通过建立多元线性回归模型，得出全国居民人均消费支出、政府预算支出和就业人口总数均对国民生产总值起促进作用，并依据所得模型提出促进GDP进一步提高的政策建议；姚玉臣利用数理统计方法，得出影响中国GDP的主要因素是居民消费水平，能源消费总量；吴金香应用多元统计经济学对影响我国GDP增长的经济因素进行因子分析。

　　目前多数学者以多元线性回归分析等计量分析方法为主，从整体分析GDP影响因素，而很少考虑影响因素之间的相关关系。并且对GDP影响因素的研究大多基于统计数据建模分析，很少与网络结构图相联系。国内外不少学者利用构建网络图模型方法研究股票市场，例如Garas等研究了复杂经济系统的网络性质，发现利用边权重过滤技术和距离变换构建的股票网络模型拓扑结构最为明显；Lee等利用互相关系数考虑股票市场中的复杂网络，在阈值的有限范围内观察到了无标度网络；杨冶辉等、周立敏等吴翎燕等利用相关系数和最佳阈值法构建了股票网络结构模型，得出沪深300成分股网络具有小世界性和无标度性。

　　由于相关系数阈值法仅能识别两者间的相关性，并不能说明条件独立，因此本文基于图模型方法，在偏相关分析和最佳阈值的基础上构建网络图结构，以GDP与九大行业为节点，相互之间的相依关系为边，进行网络图可视化，并根据中心度、网络结构对影响GDP的行业因素进行深入探讨，对不同行业间的相互依存关系进行分析。

　　一、数据说明

　　本文数据来源于《中国统计年鉴》，选取2000—2022年近23年的国内生产总值GDP统计数据进行实证分析，其中国内生产总值GDP作为被解释变量，九大行业作为解释变量，即农林牧渔业（X1）、工业（X2）、建筑业（X3）、批发和零售业（X4）、交通运输仓储和邮政业（X5）、住宿和餐饮业（X6）、金融业（X7）、房地产业（X8）、其他（X9），单位为亿元。

　　我国三大产业以人类生产活动的历史顺序和各种行业的性质划分，产品直接取自自然界的部门称为第一产业，对初级产品进行再加工的部门称为第二产业，为生产和消费提供各种服务的部门称为第三产业。即第一产业指农、林、牧、渔业，第二产业指工业和建筑业，第三产业指服务业（除第一、第二产业以外的其他各行业）。因此变量X1属第一产业，变量X2和X3属第二产业，变量X4、X5、X6、X7、X8和X9属第三产业。

　　二、基于偏相关系数和最佳阈值的网络图模型构建

　　（一）图模型理论

　　概率图模型（Probabilistic Graphical Model，PGM），简称图模型（Graphical Model，GM），是通过揭示多维随机变量的相依关系来刻画向量间的条件独立性，从而将多个变量之间关系的统计模型进行图形化，为研究高维空间的概率模型提供便利。

　　图模型是一个二元组G=<V,E>，其中G=<V,E>为拓扑图，V是点集，表示随机变量的集合，E是边集，记(i,j)∈E表示为点i、j间有边相连，—和→分别表示无向边和有向边。F是V上与G相适应的概率分布族[11]。若随机变量i，j之间不存在边，表示在分布族F中这两个随机变量之间存在某种独立性。

　　在多维变量情况下，为研究任何两变量之间的关系，而使与这两个变量有联系的其他变量保持不变，即控制其他变量的影响，去计算两变量的净相关性。因此研究变量间的条件独立性，即偏相关关系。

　　在Whittaker提出的基于多元正态假设的无向图模型中，对于零均值的多元正态分布d维随机向量Y=(Y,…,Y)'，记协方差矩阵为Σ,表达式如式（1）所示。

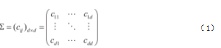
　　其中主对角线元素cii为变量Yi自身的方差；cij为两变量Yi和Yj的协方差。

　　cij=Cov(Yi,Yj)=E{[Yi−E(Yi)][Yj−E(Yj)]};i,j=1,2,...,d；

　　且Cov(Yi,Yj)=Cov(Yj,Yi)即cij=cji。

　　精度矩阵K为协方差矩阵的逆矩阵，记K=Σ−1。

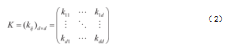
　　在变量Yij.=Y−{Yi,Yi}，i,j=1,2,....,d给定的条件下Yi和Yj的偏相关系数记为ρij.，ρij.=ρ(Yi,Yj|Yij.)。

　　可推导出Yi和Yj的偏相关系数为：

　　在多元正态分布中条件不相关等价于条件独立，故当且仅当精度矩阵K中元素kij=0时，两变量Yi和Yj条件不相关，即两变量在其他变量给定条件下是条件独立的，同时说明两变量间无边存在。表1给出变量间偏相关系数矩阵。

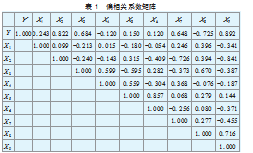
　　（二）求解最佳阈值

　　本文以GDP与九大行业作为网络中的节点，若偏相关系数，则节点i和j之间有连边，其中θ为阈值。阈值大小与构建网络连边数成反比例关系，即所选取的阈值越大，构建网络连边数越少，反之亦然。通过设立不同的阈值，结合偏相关系数，得出最大连通子图节点数。当阈值在某区间内，最大连通子图节点数变化平稳，选定最佳阈值构建网络结构图，此时所构建网络的拓扑性质稳定。

　　根据不同的阈值，推出相应的最大连通子图节点个数，并绘制折线图（见图1），观察其变化趋势。

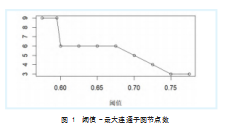
　　如图1所示，当网络结构的阈值设定在0.60~0.675之间时，最大连通子图节点个数变化稳定。此处选取平均值0.637 5为最佳阈值，为构建网络结构图做基础。

　　（三）网络中心度

　　在网络分析中，通常用点中心度（Degree Centrality）对节点中心度进行度量，来描述节点在整个网络信息传递的活跃程度。一个节点关系越广，相邻节点越多，则点中心度越大，意味着该节点在网络中越重要。用公式（4）表示。

　　其中ND(Pi)表示节点Pi的度数，即节点Pi的邻边数；n为网络节点总数，n−1表示为节点Pi的度最大时的可能值。

　　（四）网络图构建

　　结合上文所求得的偏相关系数矩阵及最佳阈值，给出基于图模型方法的网络图结构。如图2给出阈值为0.1及最佳阈值（0.637 5）下的网络图，其中节点大小与点中心度成正比，用于表示节点在网络中发挥的影响力和重要性。

　　节点的颜色由分类决定，同属第一产业的解释变量为白色，同属第二产业的解释变量为橙色，同属第三产业的解释变量为灰色，被解释变量GDP的节点用黑色表示。在图中用连线的粗细程度表示权重大小，当两节点存在正相关性用实线连接，反之虚线。

　　图2（a）为阈值0.1下的网络图结构，可将GDP与各行业间的相关关系完整呈现出来，但较为复杂，不易分析。相较之下图2（b）在最佳阈值（0.637 5）下的网络图结构更为清晰直观，将节点间的逻辑关系更为明确地展现出来，可以直观反映出影响GDP的主要因素及行业间的密切关联性。

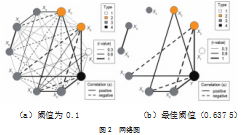
　　从图2（a）（b）中的节点大小，可看出GDP（Y）的节点均是最大的，即在所有节点中点中心度最大，邻边数最多，意味着在网络图中影响力最大。解释变量X1—X9均为被解释变量GDP（Y）的影响因素，只是影响程度不同，因此GDP（Y）在网络图中核心地位极强，与各行业间联系紧密，有着极强的影响力。

　　从图2（b）中连线分析，影响GDP（Y）的主要因素有工业（X2）、建筑业（X3）、金融业（X7）、房地产业（X8）和其他（X9），其中工业（X2）、建筑业（X3）、金融业（X7）和其他（X9）与GDP（Y）正向相关，房地产业（X8）与GDP（Y）负向相关，即当其他条件不变时，工业（X2）每平均增加一个单位，GDP（Y）也会增加一个单位；建筑业（X3）、金融业（X7）和其他（X9）同理；房地产业（X8）每平均增加一个单位，GDP（Y）会减少一个单位。房地产市场的繁荣会直接或间接地促进金融业的发展，从而推动GDP增长。但由于房地产市场过热，购房者负债累累，消费能力下降，这对GDP增长不利，因此会呈现负向相关。

　　农林牧渔业（X1）和批发和零售业（X4）均与其他节点无连线，说明二者对GDP的影响相对较弱，且与其他变量之间的联系也是极弱的。工业（X2）与金融业（X7）和其他（X9）连线较粗，关联性显著，且存在负向相关，即工业（X2）的波动会引起金融业（X7）和其他（X9）两行业的较大波动。同时由于工业化率高的地区通常以制造业为主，在经济结构中，制造业和服务业具有相对的互补性，随着服务业的发展和扩张，制造业增速相对较慢。并且在劳动力需求上，制造业与服务业的增长也呈负相关，因此出现工业化率与服务业增加值呈负相关的现象。建筑业（X3）与房地产业（X8）之间、交通运输仓储和邮政业（X5）和住宿和餐饮业（X6）之间、房地产业（X8）和其他（X9）之间关联性显著，且存在正向相关，即一方的波动会引起另一方较大的波动，一方的增加另一方也会相应增加。

　　三、多元统计方法分析

　　多元统计分析是数理统计学中重要的分支学科之一，主要是研究多变量之间的相关关系，通过建立模型对变量间的关系认识定量化。下面对GDP与行业间的相关关系进行多元统计分析。

　　（一）线性拟合模型及检验

　　首先可根据散点图初步判断各变量间可能存在一定的线性关系，从而建立如下初步的多元线性回归模型。

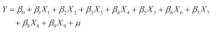
　　其中原假设：β1=β2=β3=β4=β5=β6=β7=β8=β9=0。

　　即若拒绝原假设，则认为自变量与因变量之间不存在线性关系。

　　利用R软件得出多元回归方程。

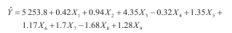
　　其中R2及调整后的R2均接近于1，且p值极小，几乎接近于0，认为线性关系显著；而在显著水平为0.1下，回归系数X2、X3、X7、X8、X9显著，X1、X4、X5、X6不显著，下面对模型进一步检验及修正。

　　（二）多重共线性检验及修正

　　多重共线性是指线性回归模型中自变量之间由于存在高度相关系数而使模型的权重参数估计失真或难以估计准确性的一种特性。下面对多重共线性进行检验及修正。

　　根据VIF方差膨胀因子法判定，VIF表示回归系数估计量的方差与假设自变量间不线性相关时方差相比的比值，当VIF超过10时，认为回归模型存在严重的多重共线性。由表2可知VIF均大于10，认为存在严重的多重共线性。

　　利用逐步回归法对变量进行筛选、剔除，从而对模型进行修正。在显著水平为0.01条件下，最终剔除变量X1、X4、X5、X6，得到最优模型：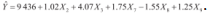

　　其中R2及调整后的R2均接近于1，且p值极小，几乎接近于0，认为线性关系显著；在显著水平为0.01下，回归系数均显著。

　　综上分析，影响我国GDP的主要因素有：工业（X2）、建筑业（X3）、金融业（X7）、房地产业（X8）、其他（X9），且工业（X2）、建筑业（X3）、金融业（X7）和其他（X9）与GDP（Y）正向相关，房地产业（X8）与GDP（Y）负向相关，这与前文中构建的网络图模型所得结论是相同的，这从统计角度验证了图模型结论的正确性。

　　四、研究结论

　　本文通过《中国统计年鉴》选取近23年国内生产总值GDP年度数据，对GDP与九大行业间的关系进行分析，以国内生产总值GDP为被解释变量，九大行业作为解释变量，即农林牧渔业、工业、建筑业、批发和零售业、交通运输仓储和邮政业、住宿和餐饮业、金融业、房地产业、其他。基于偏相关系数选取最佳阈值0.637 5，并以此构建网络图结构，以GDP与九大行业为节点，相互之间的相依关系为边，进行网络图可视化。结果显示最佳阈值（0.637 5）下的网络图结构，相较于阈值0.1下的图结构更清晰明了，可以更加直观反映出影响GDP的主要因素及行业间的密切关联性。

　　得出影响GDP的主要因素有工业、建筑业、金融业、房地产业和其他，其中除房地产业与GDP呈负相关外，其他行业与GDP呈正相关，即当其他条件不变时，工业每平均增加一个单位，GDP也会增加一个单位；建筑业、金融业和其他同理；房地产业每平均增加一个单位，GDP会减少一个单位。房地产市场的繁荣会直接或间接地促进金融业的发展，从而推动GDP增长。但由于房地产市场过热，购房者负债累累，消费能力下降，这对GDP增长不利，因此会呈现负向相关。

　　同时工业与金融业和其他行业关联性显著，且存在负向相关，即工业的波动会引起金融业和其他两行业的较大波动。同时由于工业化率高的地区通常以制造业为主，在经济结构中，制造业和服务业具有相对的互补性，随着服务业的发展和扩张，制造业增速相对较慢。并且在劳动力需求上，制造业与服务业的增长也呈负相关，因此出现工业化率与服务业增加值呈负相关的现象。建筑业与房地产业、交通运输仓储和邮政业和住宿和餐饮业、房地产业和其他关联性显著，且存在正向相关，即一方的波动会引起另一方较大的波动，一方的增加另一方也会相应增加。

　　利用网络图模型分析所得结论与多元统计方法分析所得结论相同，验证了图模型结论的正确性。但相较于多元统计方法，网络图模型使各节点间的相关关系更为清晰明确，可直观反映出影响GDP的行业因素。

        参考文献：

　　［1］赵浩然.我国GDP影响因素计量分析［J］.中国集体经济，2021（30）：12-14.

　　［2］FENG Xinke，WU Junyi，YU Huiyi.An inquiry into the influencing factors of GDP growth in our country since the reform and opening up—An empirical study based on OLS model［J］.Academic Journal of Business&Management，2023，5（11）：128-136.

　　［3］KIRA A R.The factors affecting gross domestic product（GDP）in developing countries：The case of Tanzania［J］.European Journal of Business and Management，2013，5（4）：148-158.

　　［4］姚玉臣.影响GDP增长的经济因素分析［D］.哈尔滨：哈尔滨工业大学，2015.

　　［5］吴金香.影响GDP增长的经济因素因子分析［J］.商场现代化，2015（28）：216-217.

　　［6］GARAS A，ARGYRAKIS P，HAVLIN S.The structural role of weak and strong links in a financial market network［J］.European Physical Journal B，2008，63（2）：265-271.

　　［7］LEE K E，LEE J W，HONG B.Complex networks in a stock market［J］.Computer Physics Communications，2007，177（1/2）：186-201.

　　［8］杨治辉，贾韩梅.股票收益率相关性的网络结构分析［C］//中国自动化学会控制理论专业委员会.中国自动化学会控制理论专业委员会B卷.安徽财经大学统计与应用数学学院，2011：5.

　　［9］周立敏，曹喆，朱家明，等.基于相关系数和最佳阈值的股票网络构建及应用［J］.浙江科技学院学报，2015，27（4）：256-262.

　　［10］吴翎燕，韩华，宋宁宁.基于相关系数和最佳阈值的股票网络模型构建［J］.复杂系统与复杂性科学，2013，10（4）：49-55+85.

　　［11］熊巧巧，蔡风景.基于图模型方法的我国股市网络结构分析［J］.温州大学学报（自然科学版），2017，38（4）：21-28.

　　［12］陈敏琼，彭东海.关于偏相关系数的计算公式的一点注记［J］.滁州学院学报，2014，16（2）：26-29.

　　［13］齐景超.股票市场复杂网络建模与序列分析［D］.上海：上海理工大学，2014.