【摘要】为探究公路大件运输的安全监管问题，文中基于演化博弈论及系统动力学构建以行业监管部门和大件运输企业为主体的两方博弈模型，求解系统的局部均衡点并分析其稳定策略。运用Vensim软件分别仿真静动态监管机制及调整外部变量等情况的演化博弈过程，根据仿真结果提出优化建议。结果表明:静态监管机制下不存在稳定性策略。引入动态监管机制后，系统存在稳定均衡解;适度增加罚款限额及提高公众举报概率有利于优化监管体系。

　　【关键词】公路大件运输;演化博弈;系统动力学;安全监管

　　大件运输行业是国家重点工程建设不可或缺的保障，与国民经济发展密切相关［1］。同时，大件运输具有超长、超重、装载难的特点，一旦发生交通事故，将对生命和财产造成极大的损失。“12·18沪渝高速天桥侧翻事故”造成4人死亡，8人受伤，直接经济损失逾3000万元，追溯事故主要原因为承运人违法超限运输，故意逃避监管［2］。

　　目前，大件运输的研究内容主要包括两方面:一是安全设计与评价。Palšaitis，Petraška［3］总结大件运输风险因素，认为影响其运输质量最为关键的外部因素是安全和保障。李晓东［4］从大件运输车辆可靠性、货物捆扎稳定性及行驶稳定性等三方面量化了安全指标。Petraška等［5］以大件运输时间最少和费用最低为目标，制定了考虑技术经济和运输风险的货物运输路线的选择标准，并提出评价路线的算法。李维东等［6］基于PCA改进层次分析法，为大型货物运输通道线路方案决策提供依据。柴李等［7］采用遗传算法，仿真公路大件运输弯道轮廓的通过性;二是安全管理与政策研究。何彬［8］从制度变迁的视角出发，分析大件运输制度的变化过程，运用AMOS软件分析大件运输企业管理能力与各影响因素的关系。劳恒延，黎铁良［9］通过分析大件运输安全管理的现状及问题，从政府、行业、操作等多面给予建议。Macioszek［10］介绍了波兰相关超大型货物运输的条件、类型、文件、组织方法及驾驶条件等内容，认为过境所需的许可证数量是超大型货物运输的难点。

　　综上所述，目前国内外学者大多针对大件运输过程中某一具体步骤、线路的安全影响因素、评价指标、方案优化及管理政策进行了较多探析，但缺乏从运输主体的角度出发，基于主体之间的利益关系展开安全监管研究。本文以大件运输企业与行业监管部门为研究主体，根据演化博弈理论构建系统动力学模型，对监管策略进行仿真分析。此外，探讨不同外部变量对监管体系的影响，给予相应优化建议，以期为减少公路大件运输事故发生率，为行业安全监管相关领域提供理论参考。

　　1公路大件运输安全监管的演化博弈模型

　　在公路大件运输过程中，大件运输企业与行业监管部门之间存在紧密的利益关系。两者之间的策略选择是决定大件运输是否能顺利完成的关键。

　　1．1模型假设

　　大件运输企业及行业监管部门为参与博弈的主体，公众辅助监管部门对企业进行监督。根据演化博弈理论的原理，两者均为有限理性方，故无法在博弈过程中做出最优决策。大件运输企业以实现自身利益最大化、降低成本为目标;行业监管部门需对大件运输企业实施监管以降低事故发生率。设定监管部门的策略为监管K1、不监管K2;大件运输企业的策略为遵守运输组织方案M1、不遵守运输组织方案M2(“运输组织方案”包括运前车辆、人员准备方案;路面、车辆等运输保障;线路规划;护送方案及应急预案等内容，以下简称“方案”)。博弈模型假设如下:

　　①行业监管部门作为公共管理部门，本身不获得收益。监管部门对企业实行监管所付出的成本为C1;大件运输企业不遵守方案被行业监管部门发现或被公众成功举报，部门对企业处以罚款G1，对公众给予奖励G2;如企业不遵守方案且未被发现而造成事故，将给行业监管部门带来综合损失S1。

　　②大件运输企业遵守方案所付出的成本为C2，不遵守方案所需成本为C3(C2＞C3);企业完成运输项目所获收入为E1。当企业缺乏内外部监管时，发生事故造成的损失为S2。

　　③行业监管部门实行监管概率为x，不监管的概率为1-x(0≤x≤1);大件运输企业遵守方案的概率为y，不遵守方案的概率为1－y(0≤y≤1);大件运输企业遵守方案发生事故的概率为p1，不遵守方案发生事故的概率为p2(0≤p1＜p2≤1);公众成功举报企业的概率为p3。

　　1．2模型的收益矩阵

　　基于上述假设与说明，可得到如表1所示的收益矩阵。

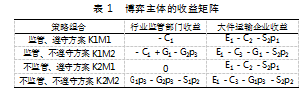
　　设行业监管部门实行监管、不监管的期望收益分别为V11、V12，根据表1所列的收益矩阵关系，可得:

　　V11=－C1 y+(－C1+G1－G2p3)(1－y)(1)

　　V12=(G1p3－G2p3－S1p2)(1－y)(2)

　　则行业监管部门平均期望

　　V1=xV11+(1－x)V12(3)

　　设大件运输企业遵守方案、不遵守方案的期望收益分别为V21、V22。根据表1所列的收益矩阵关系，可得:

　　V21=(E1－C2－S2p1)x+(E1－C2－S2p1)(1－x)(4)V22=(E1－C3－G1－S2p2)x+(E1－C3－G1p3－S2p2)(1－x)(5)

　　则大件运输企业平均期望

　　V2=yV21+(1－y)V22(6)

　　2博弈模型均衡点分析

　　2．1均衡点求解

　　根据Malthusian复制动态方程［11］，可得行业监管部门实行监管的变化率

　　f(x)==x(V11－V1)=x(1－x)(V11－V12)(7)

　　大件运输企业遵守方案的变化率

　　f(y)==y(V21－V2)=y(1－y)(V21－V22)(8)

　　将式(1)(2)代入式(7)，式(4)(5)代入式(8)，得到二维系统动力学方程组，如式(9)所示。

　　{f(x)=x(1－x)(C1－G1+G1p3+G1 y－G1p3 y)

　　{f(y)=y(1－y)(C3－C2+G1p3+G1 x－S2p1+S2p2－G1p3 x)(9)

　　当f(x)、f(y)的值均为0时，求解出5个局部均衡点，分别是(0，0)、(1，0)、(0，1)、(1，1)、(x0，y0)。其中x0=－m/G1(1－p3)，y0=h/(h+C1)。m=C3－C2+G1p3－S2p1+S2p2，h=G1(1－p3)－C1+S1p2。

　　2．2均衡点稳定性分析

　　根据Firedman理论，可用雅克比矩阵分析局部均衡点的稳定性［12］。本文提出的安全监管演化博弈矩阵如下:

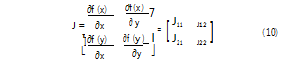
　　式(10)中，J11=(2x－1)((G1－G1p3+S1p2)y－h)，J12=x(x－1)(G1－G1p3+S1p2)，J21=－y(G1－G1p3)(y－1)，J22=－(2y－1)(m+G1(x+p3－p3 x))。当行列式Det(J)=J11 J22－J12 J21＞0且迹Tr(J)=J11+J22＜0时，均衡点稳定。5个局部均衡点所对应的取值情况如表2所示。

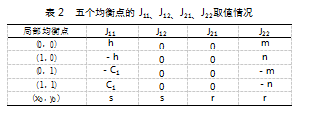
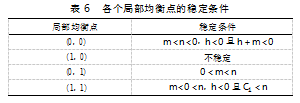
　　表2中，n=C3－C2+G1－S2p1+S2p2，s=(2x－1)(G1 y-G1p3 y+S1p2 y－h)，r=y(1－y)(G1－G1p3)。由于0≤p3≤1，故m＜n。当均衡点为(x0，y0)时，涉及的参数较多，雅克比矩阵分析较复杂，难以直接判断各特征值符号情况，故下文先针对四个纯策略均衡点在m、n不同情况下进行稳定性讨论。

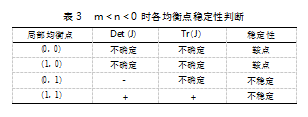
　　①当m＜n＜0时，公路大件运输安全监管演化博弈的二维动力系统各点的稳定情况如表3所示。

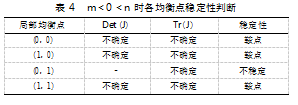
　　②当m＜0＜n时，公路大件运输安全监管演化博弈的二维动力系统各点的稳定情况如表4所示。

　　③当0＜m＜n时，公路大件运输安全监管演化博弈的二维动力系统各点的稳定情况如表5所示。

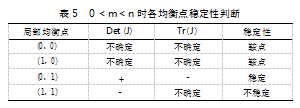
　　由表5可知，当0＜m＜n时，系统存在一个演化稳定策略(0，1)，即行业监管部门不实行监管，大件运输企业遵守方案的时候可保持系统稳定。整理上述分析结果，得到如表6所示的各均衡点的稳定条件。

　　3系统仿真

　　通过上述分析可知，不同参数取值情况会直接影响公路大件运输的策略选择，但未能反映两主体产生稳定策略的演化过程。同时，现实中两个主体均是有限理性方，行业监管部门和大件运输企业并非完全独立，两者之间的策略选择也会进一步影响彼此的策略。为解决上述问题，下文运用Vensim软件构建系统动力学模型并仿真博弈情况。

　　3．1系统动力学模型构建

　　系统动力学是研究系统反馈结构和行为的一门科学，其将系统科学理论与计算机仿真相结合。为进一步研究行业监管部门与大件运输企业之间的策略影响，需厘清各要素之间的关系并以此构建静态机制下的系统动力学模型，如图1所示。

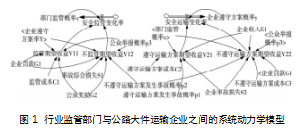
　　由图1可知，上述系统动力学模型包括2个状态变量、2个速率变量、4个中间变量、11个外部变量。其中，外部变量主要包括“企业罚款”“监管成本”“企业收入”“公众奖励”等。本文采用调研形式对事故风险因素进行分类与判定，基于2022年XX电厂定子德阳至乐山运输案例获取相关成本赋值。邀请八位相关领域的专家作为专家小组，利用DEMATEL法计算各风险因素中心度，将大件运输企业与行业监管部门对应的风险因素的中心度归一化处理后相加，以此作为对应主体的事故发生概率值。为方便仿真分析，度量单位统一设定为万元，具体取值见表7。

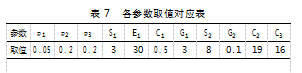
　　将表7数据代入式(9)中可解得该静态监管机制下，具有4个纯策略均衡点和1个混合策略均衡点，分别是(0，0)、(1，0)、(0，1)、(1，1)、(0．43，0．82)。

　　3．2静态监管机制仿真

　　本实验在Vensim软件7．3．5版本上运行，设定仿真参数INITIAL TIME=0，FINAL TIME=500，TIME STEP=0．1。对混合策略(0．43，0．82)进行稳定性分析，仿真结果如图2所示。

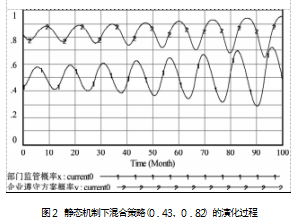
　　由图2可知，行业监管部门和大件运输企业两者相互影响，监管概率和遵守方案的概率存在大幅度波动，说明该状态下的博弈系统的混合策略均衡点不稳定，即该静态机制下不存在稳定策略。

　　3．3动态监管机制仿真

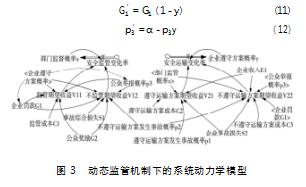
　　经上述分析可知，在静态监管机制下，大件运输企业与安全监管部门之间不存在演化稳定策略。因此，需设计动态的监管机制来实现系统平衡。大件运输企业对运输方案的遵守程度与事故的严重程度有直接关联，而事故严重程度直接影响罚款数额。此外，现实中公众举报企业的概率和企业遵守运输方案的概率也有关，企业不遵守方案概率越低，公众举报概率就越高。故可设定企业罚款G1、公众成功举报概率p3分别与企业遵守方案的概率y之间的函数关系如式(11)(12)所示。其中，G1'、p3'分别为动态监管机制下的企业罚款和公众成功举报概率，α为参数。设定企业遵守方案概率为0时，被公众举报的概率为0．7，代入式(12)得α取值为0．7。该动态机制的系统动力学模型如图3所示，虚线代表新引入关系。

　　假设参与博弈的两个主体的初始策略为(0．5，0．5)，其他仿真参数不变，得到的仿真演化结果如图4所示。

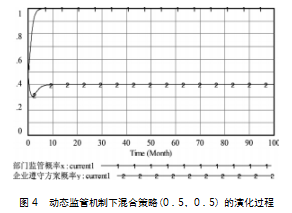
　　由图4可知，行业监管部门为减小事故发生率不断提高监管概率，企业为维持自身利益，随之增加按章运输概率，最终在(1，0．4)实现稳定。这表明在新的监管机制下，两博弈主体存在稳定策略。但此时，企业遵守方案的概率较低，事故风险率依然较高，故需要针对外部变量进行优化调整。

　　4外部变量仿真

　　4．1企业罚款

　　根据《超限运输车辆行驶公路管理规定》可知，针对车辆超载的处罚G1最高为3万元。现分别提高限额为4，5，6万元进行仿真，得到如图5所示的仿真结果。

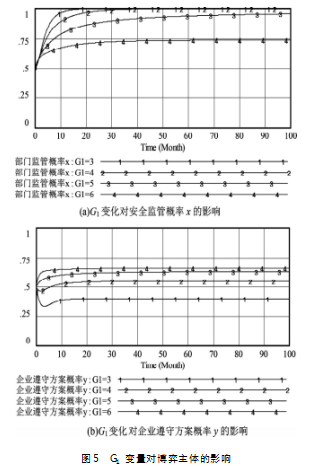
　　由图5(a)可知，当其余参数变量保持一致时，企业罚款限额增加会减缓行业监管部门提升监管概率的速率。图5(b)中，企业遵守方案的概率随着企业罚款的增加而增加，最高在y=0．662时保持稳定。这是因为在提高罚款时，企业为减少自身企业事故损失和罚款支出，会选择提高自身按章运输的概率。此时，行业监管部门会疏忽监管，逐渐降低监管概率。

　　4．2公众成功举报概率

　　为探析公众举报概率对博弈系统的影响，保持其余参数不变，仿真p3值分别为0．3，0．4及0．5时的系统演化情况，结果如图6(a)(b)所示。同时，考虑不同罚款限额与公众举报概率对主体策略选择的影响，仿真G1=6时的演化情况，如图6(c)(d)所示。

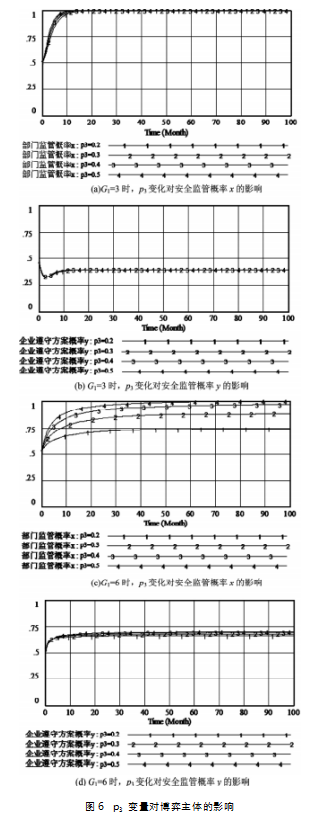
　　由图6(a)(b)可知，当企业罚款限额为3万元时，增大公众举报概率会提高行业监管部门实行监管的速率，对企业是否遵守方案的概率无明显影响且两个主体均在短时间内实现稳定。由图6(c)(d)可知，当企业罚款限额提升至6万元时，公众举报概率越高，部门实行监管的概率也越高，此时企业会小幅度增加遵守方案的概率，最终在y=0．7时保持稳定。对比图6(c)和图5(a)可知，在高罚款限额基础上增加公众成功举报概率才能明显提高部门监管概率，整体提升监管系统稳定性。因此，公众监督对行业监管部门起到了良好的补充作用。

　　5结论

　　本文运用演化博弈理论和系统动力学，构建了以行业监管部门和大件运输企业为利益主体的两方博弈模型，运用Vensim软件分别仿真了静动态监管机制下的演化过程，最后基于仿真结果提出对策与建议。本文得出的主要结论与建议如下:

　　①当监管策略处于静态时，整个系统不存在稳定性。引入企业罚款与企业遵守方案的概率成函数关系的动态监管机制以后，监管系统具备稳定性。监管部门应对大件运输企业进行定期检查，对不符合安全标准的运输企业按程度进行处罚。

　　②增加惩罚力度有利于加强监管效果。在罚款金额较低时，增加公众举报概率对系统无明显影响。当罚款额度提高到6万元时，公众在安全监管系统中发挥作用。公众举报概率越高，行业监管部门的监管力度也越大。但罚款限额过大时，反而可能会引起监管部门的工作懈怠而降低安全监管概率，不利于整个监管体系发展。需平衡惩罚力度和公众举报概率之间的关系，优化动态监管机制。建议交通运输管理部门针对不同的违章事故细化处罚规定并提升惩罚力度，加大对大件运输企业的约束。

　　③提升公众对企业的举报概率有利于促进行业监管部门实行监管，提高企业遵守方案的概率，最终在0．7时处于渐进性稳定状态。故政府需要重视并提高社会公众的监督能力，加大宣传力度与关注度，并在公众场合、社交媒体上定期传达监管部门对制约企业违章运输的重要性以进一步维护监督能力;加强*息公开，构建大件运输数据库，鼓励公众对*息进行查询并在必要时提供奖励。

　　在实际的大件运输过程中，涉及的利益主体不仅限于本文所提出的大件运输企业和行业监管部门两方，引入新的利益主体(如员工)和相关影响因素参与博弈分析是后续的研究重点。

　　［参考文献］

　　［1］崔优梅，曾珠，孙文瑞．基于DEMATEL－ISM的道路大件运输安全风险因素分析［J］．安全，2022，43(06):31－36.

　　［2］鄂州市人民政府．沪渝高速(G50)花湖互通D匝道“12·18”较大桥面侧翻事故调查报告［EB/OL］．

　　［3］Palšaitis R,Petraška A．Heavyweight and oversized cargo transportation risk management［J］．Transport and Telecommunication，2012，13(1).

　　［4］李晓东．大件运输公路安全性评价与路径决策［D］．西安:长安大学，2020.

　　［5］Petraška A，ĈižiūnienēK，et al．Algorithm for the assessment of heavyweight and oversize cargo transportation routes［J］.Journal of Business Economics and Management，2017，18(6).

　　［6］李维东，郭蕊，张磊，等．基于PCA改进层次分析法的多目标大型货物运输通道选择［J］．中国安全生产科学技术，2021，17(02):

　　［7］柴李，曾传华，邓子杰，等．公路大件运输车组弯道轮廓通过性分析［J］．西华大学学报(自然科学版)，2023，42(2):20－27.

　　［8］何彬．中国公路大件运输企业管理能力提升研究———基于制度变迁的视角［D］．成都:西华大学，2021.

　　［9］劳恒延，黎铁良．大件运输安全管理探究［J］．中国公路，2020(15):118－119.

　　［10］Macioszek E．Conditions of oversize cargo transport［J］.Scientific Journal of Silesian University of Technology.Series Transport，2019，102.

　　［11］Jorgen W．Evolutionary Game Theory［M］．Shanghai:Gezhi Press，2015:35－50.

　　［12］Friedman D．Evolutionary games in economics［J］.Econometrica，1991，59(3):637－666.