摘要：文章通过分析连锁超市部分商品的销售特征，采取传统时间序列法、神经网络模型（ANN）两类基础方法对较有代表性的销售数据序列进行预测。文章将对原有的直接多步（Direct Multi-Step Ahead，DMSA）预测思路进行改进，采用改进的直接多步预测法对销量进行三步超前预测和五步超前预测，并将结果与采用DMSA、间接多步预测（Recursive Multi-Step Ahead，RMSA）和可变时间尺度法（Variable Time Scale，VTS）的实验结果进行对比，发现改进的直接多步预测法的预测精度有了一定的提升。

　　关键词：零售；直接多步预测；神经网络；时间序列

　　在连锁超市的补货决策过程中，经营者比较关心未来某一段时间内的商品预计消耗量，支持他们做出合理的补货和订货计划，因此单步预测（single-step ahead prediction，SSA）往往不能够充分满足预测的要求，他们需要一种方法能够在已知历史信息的前提下，预测出未来某段时间内商品的总体销量，而学术界对于超市零售商品的多步预测（MSA）研究乏善可陈，本文的研究目的就是为连锁超市商品销量的多步预测探寻出一个高效、准确的方法。

　　单步预测意为对未来一个预测序列的时间单位内的数据进行预测，是预测技术研究的基础；多步预测则是对单步预测方法的合理应用。常见的MSA多发源于三种思想：直接多步预测、间接多步预测和可变时间尺度。陆建山等[1]通过对预测误差序列的预测，回馈到原目标序列上实现对误差的控制。沈坤等[2]提出一种有限控制集MSA算法，实现了对多步预测误差较为有效的控制。张日东等[3]采用神经网络模型将非线性MSA进行分解，转化为一系列线性多步预测的过程。范峰辉等[4]在多步预报误差的基础上引入了跟踪误差项。Silveira等[5]研究了在长期预测背景下的广义最小方差控制模型，使用丢番图方程对此进行了优化。章登义[6]针对时间序列MSA问题提出使用聚类隐马尔科夫模型解决问题，实现对序列的分段，不同的分段对预测目标具有不同的影响。杨淑莹等[7]利用粒子滤波对多步预测模型进行优化。鞠增伟[8]利用广义预测控制对未来多步模型的输出施加影响以控制预测精度。以上学者均是利用一定方法降低了RMSA过程中所积累的误差。谢景新等[9]利用经验模式分解对目标序列进行分解，之后采用神经网络和混沌分析法进行直接多步预测。杨臻明等[10]提出了基于独立模型的非线性时间序列多步超前预测法，实际上是利用了ANN的学习能力，本质上是属于DMSA思想。钟美霞[11]使用数据预处理的方法对时间尺度进行了划分，将MSA转化为了SSA。Chandra等[12]对直接多步预测法进行了一定的改进，但是并没有提及训练时间的长度对实用性的降低。Giorgi等[13]使用数据成组处理最小二乘支持向量机（LS-SVM）预测法分别结合DMSA、RMSA和组合多步预测进行了实验，然而没有去验证几种MSA思想之间相对效果的好坏。

　　本文研究的MSA解决方法同样是基于时间序列预测法。部分学者使用时间序列法和神经网络模型对零售超市商品销量进行预测研究[14-15]。本文提出了一种改进的直接MSA模型，目的是避免RMSA迭代误差的同时提升DMSA对最近信息的学习性能。

　　一、零售商品销量的多步预测

　　（一）间接多步预测法

　　以单因素时间序列为研究对象的单步预测是指：用当前时刻t前若干个观测值作为模型的输入数据，得到t+1时刻的预测值，表示为：

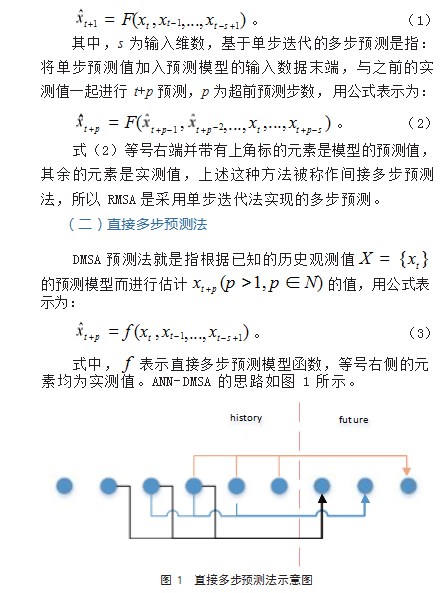
　　如上代表了一个输入变量长度为3，超前预测步数为3的神经网络预测模型。

　　（三）可变时间尺度一步外推预测法

　　VTS一步外推预测的核心思想就是通过多时间尺度（multiple time scales，MTS）理论对历史实测数据进行预处理，以预测目标时间尺度作为历史数据的最小时间单位，进而将MSA问题转化为SSA问题。因为该法只可得到未来一段时间内的总体预测值，所以该方法使用的基本前提是：问题不要求得到未来目标时间段内某一时间节点上的预测值。计算公式可以表示为：

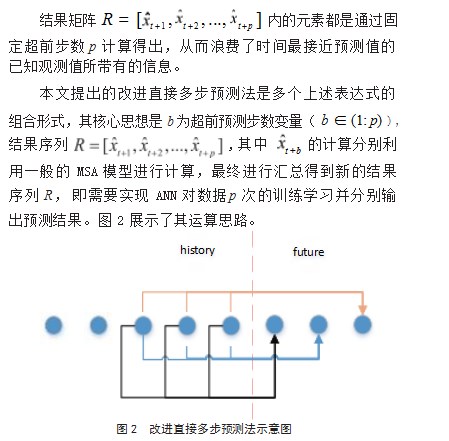
　　1.算法设计

　　Step 1：设置测试数据个数e，作为最外层循环次数，对原序列最后e个数据分别进行测试，本层所执行的操作是将输入样本进行处理：原序列为X={x1,x2,...,xt}，本次循环使用序列为X={x1,x2,...,xt−ω+1}，w为当前循环次数。

　　Step 2：设置超前预测步数p，取b∈(1:p)作为次外层循环，目的是进行分阶段独立预测。

　　Step 3：ANN输入维度设置为s，对序列进行相空间重构处理得到矩阵A。

　　Step 4：显然，矩阵左侧s列作为训练输入数据，右侧一列作为期望输出序列，利用RBF网络进行训练，设置目标精度和径向基函数传播速度等参数，开始训练。

　　Step 5：训练结束并输出预测结果。

　　Step 6：设置长度对应超前预测步数p最终结果序列R，每阶段的输出预测结果数为p，每阶段的预测结果序列取其最后一个元素即第p个元素输入最终结果矩阵R的相应位置，次循环完成。

　　Step 7：通过结果序列与目标序列之间的比较可求出相对误差。

　　Step 8：针对每个最外层循环分别执行上述步骤，最终得到平均相对误差，算法测试结束。

　　2.实验设计

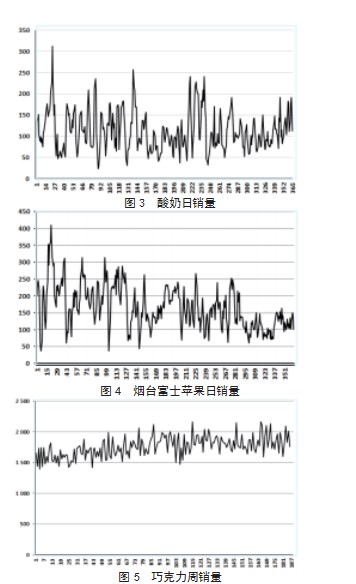
　　为了能够透彻地研究各种预测方法的优缺点，本文同时采用三组预测难度较小的周销量数据和两组随机性更高的日销量数据作为预测目标，其目的有两点：一是暴露出多种预测方法分别在不同数据背景下的多步预测过程中的优劣，方便确定适用范围；二是由于日销量预测的高精度预测更加难以达成，因此更具实验价值。图3—7中横轴为天数，纵轴为数量。

　　本文选择的SSA方法包括RBF网络模型、BP网络模型、ARIMA模型和移动平均法，分别结合RMSA、DMSA、VTS和改进的直接多步预测几个思路，采取时间序列预测方式进行了多次实验。

　　其中ARIMA模型因为其数学方法的特殊性本身具有多步预测的功能，所以无分直接和间接多步预测；只针对两种具有学习性的ANN采用改进的直接多步预测法进行实验。

　　衡量预测结果好坏的标准采用MAPE（平均相对误差）。本次多步预测实验的误差计算方式是对超前预测步数内的预测值和实测值分别进行求和再进行比对的，公式如下。

　　为了令预测结果更具说服力，本文设置了一定的测试样本长度e=20，数值e也代表了针对特定数据的多步预测实验次数，并且每次实验的预测目标不同。其中BP算法每次测试结果均取十次实验平均值。另外将糖果周销量的输入序列更改为原序列的前155个数据，测试样本数仍保持为20，此举是为了保证实验有效性的同时降低无谓的工作量。几种预测方法组合形式如表1所示。

　　3.实验结果

　　第一，三步超前预测结果（见图8）。结论：一是改进直接多步预测法在几种数据上的应用较为成功，预测结果相比直接多步预测模型的精度有明显提高；二是单从RBF网络模型的维度来看，RMSA的效果几乎是最差的；三是单从ARIMA模型的维度来看，VTS均拉低了其预测精度。

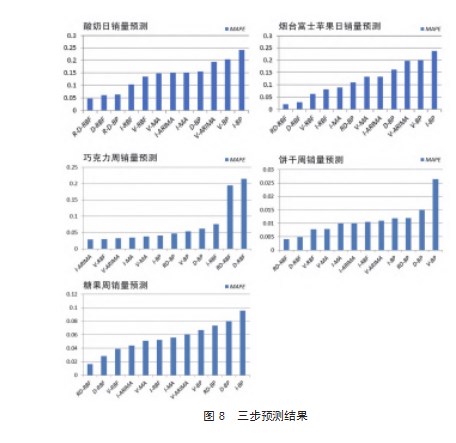
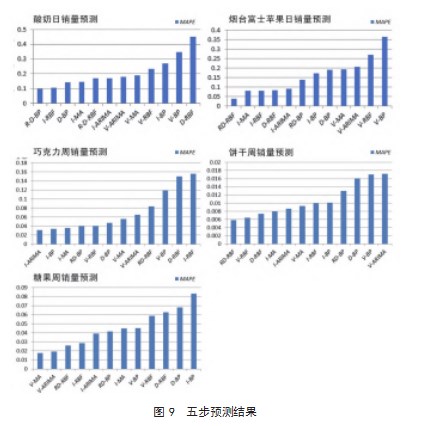
　　第二，五步超前预测结果（见图9）。结论：一是，随着预测步数的增加，改进的直接多步预测法取得的效果明显更好；二是，VTS的作用慢慢突出；三是，ARIMA算法模型对于具有直线性或周期性趋势的序列预测效果较好。

　　二、结语

　　本文使用多种预测方法和多步预测思路组合交叉，分别对几种具有代表性的商品销量进行了反复的实验，实验的主要结果表明改进的直接多步预测法相比原方法有着不同程度的进步，在不同数据的预测试验中也取得了较优的效果。本文所提出的改进直接多步预测法缺点在于训练时间较长，因此不适用于超前步数较大的预测问题，而连锁超市商品销量的超前预测步数较短，其训练时间增加有限，因此本文认为该方法对于连锁超市零售商品的预测具有较好的实用性。

　参考文献：

　　［1］陆建山，王昌明，张爱军，等.基于混沌时间序列的多步预测方法研究［J］.测试技术学报，2012，26（1）：15-19.

　　［2］沈坤，章兢，王坚.一种多步预测的变流器有限控制集预测模型控制算法［J］.中国电机工程学报，2012（33）：37-44.

　　［3］张日东，王树青.基于神经网络的非线性系统多步预测控制［J］.控制与决策，2005（3）：332-336.

　　［4］范峰辉，田学民，尚林源.基于多步预报误差的带约束模型预测控制器性能评价方法［J］.上海交通大学学报，2015（11）：1696-1700.