摘要:文章介绍了多面体外接球问题的一般求解方法,并通过举例对一些复杂的球问题进行剖析.

　　关键词:多面体；外接球；立体几何

　　与几何体有关的球问题是立体几何的重点,也是高考考查的热点和难点,这类问题能充分考查学生的直观想象、数学抽象、逻辑推理核心素养,特别是对于多面体的外接球问题,各种文献和资料都有介绍,并且归纳和总结了各种不同的解题模型,这样不仅增加了学生的记忆负担,而且从高三的实际教学情况看,效果并不好,因此需要对这类问题探求通法求解.

　　1多面体外接球问题

　　求解多面体外接球问题主要涉及到如下知识:

　　球心O与截面圆圆心O1的连线垂直于截面圆,设球的半径为R,截面圆O1的半径为r,球心O与圆心O1的距离OO1=d,如图1,则有R2=r2+d2,

　　设AB为圆O1的一条弦,M为AB的中点,则OM⊥AB.

　　这里包含以下三层含义:

　　(1)对于多面体的外接球,球心为过多面体各个面的外心且垂直该面的垂线的交点,特别地,正多面体的外接球的球心在高上;

　　(2)过球心作球内接多面体某个面的垂线,垂足为该面的外心;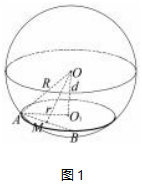

　　(3)球心到球内接多面体面的距离d=R2-r2.

　　对于外接圆半径的求法:当多面体的某个面为直角三角形时,其外接圆的圆心O1为斜边的中点;若是一般的三角形则可借助正弦定理确定外接圆的半径.

　　例1已知三棱锥P-ABC,若PA⊥面ABC,AC=BC=4 3,AB=8,PA=4,则三棱锥P-ABC外接球的表面积为.

　　解析在△ABC中,AC=BC=4 3,AB=8,

　　由余弦定理,得cosC=(4 3)2+(4 3)2-82=2×(4 3)2=.故sinC=.故△ABC外接圆的半径为r=·=3 2.

　　△ABC外接圆的圆心为O1,三棱锥P-ABC

　　外接球的球心为O,由于PA⊥面ABC,OO1⊥面ABC,故OO1∥PA,且OP=OA=R,于是OO1=PA.

　　所以三棱锥P-ABC外接球的半径

　　R=r2+(1 PAö2=.

　　所以三棱锥P-ABC外接球的表面积为4πR2=88π.

　　点评对于有一条棱垂直一个面的多面体的外接球问题,以三棱锥为例:三棱锥P-ABC,若PA⊥面ABC,则该三棱锥的外接球的半径R=r2+PA其中r为△ABC外接圆的半径.

　　特别:(1)若△ABC为直角三角形(A为直角),

　　则r2=1(AB2+AC2),故R=1,

　　这便是墙角模型,这与将三棱锥P-ABC补成长方

　　体所得结论一致;

　　(2)若△ABC为直角三角形(以B为直角为

　　例),则有r2=(AB2+BC2)=AC2,于是R=,这便是鳖臑模型,这与将三棱锥P-ABC补成长方体所得结论一致.

　　例2如图2,在三棱锥P-ABC,△PAC是以AC为斜边的等腰直角三角形,且CB=2 2,AB=AC=6,二面角P-AC-B的大小为120°,则三棱锥P

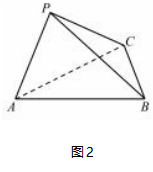
　　ABC的外接球表面积为().A.πB.10πC.9πD.(4+2 3)π解析根据题意,作出图形,如图3所示,

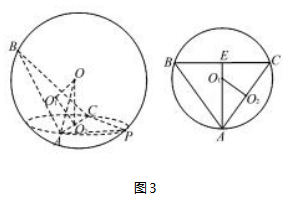
　　因为△PAC是以AC为斜边的等腰直角三角形,

　　所以△PAC的外心在AC中点,设为O2,设△ABC的外心为O1,BC中点为E,AO1=r1,因为AB=AC=6,

　　所以O1必在AE连线上.

　　则2r1===3.即r1=.因为两平面交线为AC,O1为平面ABC所在圆面中心,

　　所以O1 O2⊥AC,O1 O2=r-(AO2)2=.

　　又因为二面角P-AC-B的大小为120°,

　　PO2⊥AC,

　　所以∠PO2 O1=120°,∠OO2 O1=30°.

　　所以OO2=O1 O2×=1,

　　锥体P-ABC外接球半径R2=AO2=(AO2)2+(OO2)2=2+1=.则三棱锥P-ABC的外接球表面积为S=4πR2=10π,故选B.

　　点评一般地,对于三棱锥P-ABC,二面角P-AC-B的大小为θ,则三棱锥P-ABC的外接球的半径R可由以下方法求出:

　　(1)分别求出△ABC和△PAC的外接圆半径r1,r2,其外接圆的圆心分别记为O1,O2;

　　(2)分别过点O1,O2作面ABC和面PAC的垂线,两垂线的交点O即为三棱锥P-ABC的外接球的球心;

　　(3)取AC的中点Q,则O1 Q⊥AC,O2 Q⊥AC,故∠O1 QO2为二面角P-AC-B的平面角,即∠O1 QO2=θ;

　　(4)在四边形PO1 QO2中,O1 Q=

　　rACO2 Q=rAC在△O1 QO2

　　中利用余弦定理算出O1 O2,再由正弦定理算出其外接圆直径1i;

　　(5)由于O,O1,Q,O2四点共圆,故OQ2=

　　O2 Q2,于是三棱锥P-ABC的外接球的

　　半径R2=OQ2+r.

　　特别:当θ=90°时,R=r+rAC

　　例3已知球O的半径为2,球心O在大小为60°的二面角α-l-β内,二面角α-l-β的两个半平面分别截球面得两个圆O1,O2,若两圆O1,O2的公共弦AB的长为2,E为AB的中点,四面体OAO1 O2的体积为V,则下列结论中正确的有().

　　A.O,E,O1,O2四点共面B.O1 O2=

　　C.O1 O2=D.V的最大值为

　　解析因为公共弦AB在棱l上,连接OE,O1 E,

　　O2 E,O1 O2,OA,如图4,则OE=OA2-AE2=3.

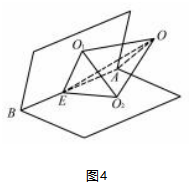
　　因为二面角α-l-β的两个半平面分别截球面得两个圆O1,O2,O为球心,

　　所以OO1⊥α,OO2⊥β.

　　又O1 E⊂平面α,O2 E⊂平面β,

　　所以OO1⊥O1 E,OO2⊥O2 E.故O,E,O1,O2四点共圆,故选项A正确;因为E为弦AB的中点,故O1 E⊥AB,O2 E⊥AB.故∠O1 EO2即为二面角α-l-β的平面角.所以∠O1 EO2=60°.

　　故O1 O2=OEsin60°=,故选项B错误,选项C正确;

　　设OO1=d1,OO2=d2,

　　在△OO1 O2中,由余弦定理可得,

　　O1 O==d+d+d1 d2≥3d1 d2.

　　所以d1 d2≤.

　　故S△OO1O2≤.

　　所以V=·AE·S△OO1O2≤,当且仅当d1=d2时取等号,故选项D正确.

　　故选ACD.

　　2与球相关的综合问题举例

　　例4如图5,在棱长为2的正方体ABCD-A1B1 C1D1中,点E是棱DD1的中点,点F在正方体表面上运动.以下命题正确的是().A.侧面CDD1 C1上不存在点F1,使得B1 F1⊥CD1B.点D到面A1BE的距离与点C1到面A1BE的距离之比为C.若点F满足B1 F∥平面A1BE,则动点F的轨迹长度为2 5D.若点F到点A的距离为2 21则动点F的轨迹长度为π

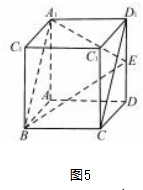
　　解析对于A选项,当F1是CD1的中点时,根据正方体的性质可知B1 C=B1D1.

　　所以△B1 CD1是等腰三角形.

　　所以B1 F1⊥CD1,所以选项A错误.

　　对于C选项,设G,H分别是CC1,C1D1的中点.

　　由于GH∥CD1∥A1B,GH⊄平面A1BE,A1B⊂平面A1BE,所以GH∥平面A1BE.由于B1 G∥A1E,B1 G⊄平面A1BE,A1E⊂平面A1BE,所以B1 G∥平面A1BE.

　　由于GH∩B1 G=G,

　　所以平面B1 GH∥平面A1BE.

　　所以满足B1 F∥平面A1BE的点F的轨迹为△B1 GH,所以轨迹长度为B1 G+B1H+GH=5+5+2=2 5+2,故选项C错误.

　　对于B选项,取CD的中点F,则EF∥A1B.连接C1D交EF于点G,易知C1 G∶GD=3∶1.故点D到面A1BE的距离与点C1到面A1BE的

　　距离之比为,故选项B正确.

　　对于D选项,AB1=AC=AD1=2 2<2

　　所以点F不在平面ABB1A1、平面ADD1A1、平面ABCD内.

　　设F(x,y,z),则AF 2=x2+y2+z2=.

　　令z=2,则x2+y2+4=,x2+y2=,=∈(2,2 2).

　　此时点F的轨迹是平面A1B1 C1D1内,以点A1为圆心,半径为4 3圆心角为π的圆弧.

　　同理可得点F在平面CDD1 C1、平面BCC1B1内

　　的轨迹也是半径为4 3圆心角为π的圆弧,所以点

　　F的轨迹长度为3××=π,故选项D正确.

　　点评本题的难点在D选项,除了本题的坐标法外,由于AA1⊥面A1B1 C1D1,故点F在平面A1B1 C1D1内的轨迹是以点A1为圆心,半径为

　　(2ö2-22=4 3圆心角为π的圆弧.è3ø3,6

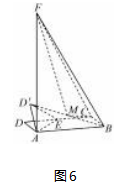
　　例5如图6,已知矩形ABCD,AB=3,AD=1,AF⊥平面ABCD,且AF=3,点E为线段DC(除端点外)上的一点.沿直线AE将△DAE向上翻折成△D′AE,M

　　为BD′的中点,则下列说法正确的有().A.三棱锥A-BCF的体积为

　　B.当点E固定在线段DC某位置时,则D′在某圆上运动

　　C.当点E在线段DC上运动时,则D′在某球面上运动

　　D.当点E在线段DC上运动时,三棱锥A-

　　BCF的体积的最小值为

　　解析由等体积法,得

　　VA-BCF=VF-ABC=××3×3=3≠3 3

　　故选项A错误;

　　当固定点E时,由DA⊥DE,可知点D在以AE为直径的圆上运动,故选项B正确;

　　当点E在线段DC上运动时,AD′=1保持不变,即点D′的轨迹为以点A为球心,半径为1的球面的一部分,故选项C正确;

　　因为SΔBCF=×BC×BF=×1×=3,

　　所以求三棱锥M-BCF的体积的最小值即求

　　点M到平面BCF距离d1的最小值,即求点D′到平面BCF距离d的最小值,且d1=d.

　　如图7,过点A作BF的垂线,垂足为点H,可得AH⊥平面BCF.

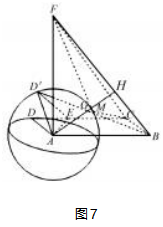
　　因为点D′在以点A为球心,半径为1的球面上运动,则点D′到平面BCF距离的最小值为d=AH-1=-1.

　　所以d1=d=.所以三棱锥M-BCF的体积的最小值Vmin=S△BCF×d1=,故选项D正确.

　　点评本题的难点在于点E的轨迹的确定,对于D选项,类比圆的知识可知,球面上一点到球外一平面的最短距离为球心到该平面的距离减去球的半径.

　　参考文献:

　　[1]鞠火旺.例谈三棱锥外接球问题的求解策略[J].中学生数学,2021(13):20-22.

　　[2]廖永福.多面体的外接球问题的若干解法[J].数理化解题研究,2019(28):34-36.

　　[3]荆志强.多面体外接球问题处理的策略探究[J].理科考试研究,2019,26(13):15-21.