摘要:文章阐述了隐含条件在初中数学解题中的重要性，并结合例题对隐含条件发掘的途径进行了详细的研究.

　　关键词:隐含条件,解题教学,发掘路径

　　在引导学生解决数学问题时，需要与已知条件相结合，但在多数题目中，已知条件并非全部明确给出，甚至一部分已知条件隐含在题目中．在这种情况下，如果学生在解题的时候，忽视了已知条件，无法将其全部挖掘出来，就会导致学生在解题时面临种种困难，甚至导致解题出现错误．鉴于此，唯有肯定隐含条件在解题中的价值，指导学生在日常解题中掌握隐含条件的发掘方法，才能真正提升学生的数学解题能力.

　　1初中数学解题教学中隐含条件的挖掘价值分析

　　在数学题目中，隐含条件与明显条件相对，属于一种比较特殊的条件，往往没有在题目中明确给出，但学生可从题中的条件推理出来，具备极强的隐蔽性．在初中数学解题中，隐含条件虽然没有明确给出，但却是解题的关键．具体来说，在初中数学解题教学中，充分发掘隐含条件具备十分重要的价值.

　　1．1有助于学生建立系统化的认知结构

　　教师在带领学生对隐含条件进行挖掘的时候，常常从多个角度出发，围绕题目进行横向、纵向思考．这拓展了学生的知识面，逐渐形成了一套完整、系统化的认知结构，为学生更好地学习数学奠定了坚实的基础.

　　1．2有助于提升学生的解题效率和创新思维能力

　　初中数学教师在优化解题教学时，通过对隐含条件的发掘，可将初中数学知识点直观、准确地展示在学生的面前，提升了学生的思维品质，有效避免了学生解题中出现的生搬硬套现象，使学生快速、准确解答数学题目，有效提升了学生的解题效率．另一方面，学生在挖掘题目隐含条件的过程中，培养了发散思维能力，提高了学生的创新思维能力.

　　1．3有助于锻炼学生的思维能力

　　初中生正处于思维能力发展的关键时期．基于数学学科的特点，学生在挖掘题目隐含条件的过程中，逐渐学会了在题目分析中独立思考，逐渐养成了“多看、多思、多分析”的习惯，在思考和分析的过程中，逐渐形成了严谨的数学思维能力［1］.

　　2初中数学解题教学中隐含条件的发掘路径分析

　　2．1基于数学概念挖掘隐含条件，明确解题思路

　　在初中数学解题中，部分隐含条件常常存在于数学概念当中．这些隐含条件是数学概念成立的根本条件，也是学生顺利解决问题的关键．但在题目中，这些条件并未明确给出．鉴于此，教师在引导学生挖掘隐含条件时，就应以数学概念作为切入点，对其展开深入、全面地分析，依据数学概念的特定条件，对题目中的信息进行综合，以此作为解决数学题目的关键点．例如，在“应用一元二次方程解题”的教学中，给出题目:关于x的方程(k－1)x2-1－kx+=0存在两个实数根，求k的取值范围．学生在分析中，根据题目中给出的“方程存在两个实数根”，可判断方程是一元二次方程．因此可得k－1≠0，这是基于一元二次方程概念给出的条件．同时，在这一数学概念中还有一个容易被学生忽视的隐含条件，即:应有意义，据此可判定出1－k=0．如此，通过概念找出隐含条件，可使学生借助不等式进行求解.

　　再比如，已知函数y=mx2－6x+2的图像和x轴只有一个公共点，求m值．学生解答的过程中，如果不认真审题，对函数概念、性质不够了解，就会将其误认为是二次函数;但函数中的二次项系数是含参数的，如果m=0，此时函数是一次函数．在这种情况下，学生解题时，唯有对“一元二次函数”的概念形成深刻地认知，才能充分挖掘题中的隐含条件，围绕m是否为零展开分类讨论，最终完成对题目的完整解答［2］.

　　2．2基于题设挖掘隐含条件

　　在初中解题教学中，题设信息是学生解题的关键．但在解题中，学生常常忽视题设中的部分内容，忽视对题设内容的全面深刻分析．在这种情况下，学生的解题难度随之增加，甚至出现了不理解数学题目的现象，严重制约了学生的解题效果．鉴于此，在带领学生挖掘题目隐含条件时，应带领学生分析题设内涵，找出其中蕴含的隐藏条件，并以此作为切入点进行解题训练．例如，在“等腰三角形”的教学中，为了培养学生的解题能力，教师给出题目:等腰三角形DEF中，DE的长度是3，DF和EF的长度分别是方程x2－10x+a=0的两个根，求a的值．学生在面对这一问题时，常常出现无从下手的现象．其实在题设中，就包含一定的隐含条件，这是学生解题的关键．鉴于此，教师在引导学生解题时，就要对题设进行仔细阅读和分析，从题设中找出相应的关系:在题目中给出了等腰三角形DEF，从中便可得出两种情况，即:假设DE是三角形的腰，根据题设中的含义即可得知DF+EF=10，DE=DF=3，则EF=7．同时，还应指导学生结合三角形进行分析，利用两边之和大于第三边的性质，对假设进行推断，明确三角形不成立;由此可推断出DE是等腰三角形的底，则DF+EF=10，因此，DF=EF=5，并由此推断出a=25．如此，通过分析题设中的隐含条件，便于学生掌握解题的关键点，提升学生的解题效率［3］.

　　2．3基于数学关系发掘隐含条件

　　在初中数学解题中，数学题目中常常蕴含着大量的数学关系，而这些数学关系中也存在隐含条件．因此，教师在引导学生挖掘隐含条件时，就应聚焦这些数学关系，从中分析出隐含条件，并据此对知识内容进行系统化的整理，最终形成完整的知识结构，并用其解题．例如，在“二次根式”教学中，根式化简问题尤为重要，并且学生在解题时，常常忽视偶次根式的被开方数是非负数的条件，使学生解决这类问题时走进误区．在

　　有意义才能进行．而学生在上述化简中，正是忽略了这一点，导致其解题时出现错误．因此，教师在引导学生挖掘隐含条件时，应从数学关系出发，从中找到全新的解题思路，并以此完善学生的知识体系，最终完成对题目的高效解答.

      2．4基于数学公式和定理发掘隐含条件

　　在初中数学学习中，公式和定理不仅是学习的关键，也是学生解题的突破口．但公式和定理都有一定的使用范围、适用条件，同时其中也包含了大量的关键信息，是学生解决相关数学问题的关键．通常，学生在解题的过程中，一旦忽视了公式和定理中的隐含条件，就无法在解题时找到突破口，甚至出现解题错误．因此，在优化解题教学时，应以此出发，引导学生围绕公式和定理进行分析，挖掘其中隐含的条件，以便于学生快速找到解题的突破口．例如，解方

     2．5基于图形挖掘隐含条件

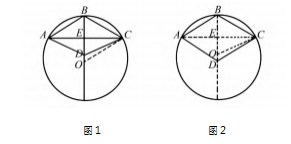
　　在初中数学学习中，几何知识不仅是初中数学学习的重点，也是初中数学学习的难点，几何图形中还蕴含着大量的隐含条件．鉴于此，教师引导学生挖掘题中的隐含条件时，必须要借助数形结合的思想，引导学生围绕几何图形进行分析，从中挖掘出隐含条件，以便于学生的解题过程更加简单，进而高效率解决数学问题．例如，已知点A、C是半径为3的圆周上的两点，点B是弧AC的中点，以线段BA、BC为邻边做菱形ABCD，顶点D恰恰在圆直径的三等分点上，则菱形的边长为多少?题目存在一定的陷阱，其中存在隐含条件．因此，在对其进行解决的时候，用数形结合思想，画出图形．但题目存在一个隐含条件，即:D点位于直径三等分点上，但并未说明是三分之一处，还是三分之二处，应以此作为切入点，对其进行分类讨论［5］．在解题的时候，围绕点D在直径的三分之一处、直径的三分之二处分别作图(如下图1、2所示)，并展开讨论．当D位于直径三分之一处时，设E为BD中点，根据题目中的条件可得出BD=×6=2，DE=BE=1，同时，结合题目条件，可得出OE=2，最终得出BC的长度;当D位于直径三分之二处，可依据题目条件，得出BD=4，且DE=BE=2，最终得出答案.综上所述，解题教学是初中数学教学的重中之重，鉴于数学学科的特点，题目中常常存在大量的隐含条件，不仅制约了学生的解题效率，甚至导致学生频频出现解题错误．鉴于此，在日常的解题教学中，必须要带领学生多角度、多层次、多方面挖掘其中的隐含条件，使得学生在隐含条件的辅助下，快速找到解题的突破口，最终完成对题目的高效解答.

参考文献:

　　［1］陈海平．化“隐”为明巧解题:谈隐含条件在初中数学解题中的价值［J］．数理化解题研究，2022(17):59－61.

　　［2］张翔．浅析初中数学解题中隐含条件的应用［J］．数理化解题研究，2022(11):14－16.

　　［3］濮维．谈隐含条件在初中数学解题中的重要作用［J］．数学之友，2022(04):76－78.

　　［4］王志军．发掘隐含条件助力数学解题:初中数学解题教学中隐含条件的应用［J］．数理化解题研究，2021(32):6－7.

　　［5］王从利．初中数学解题教学中隐含条件的应用思考［J］．数学大世界(上旬)，2021(11):21－23.